See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
Probability Theory 101
- Review the basic notion of probability theory that we will use.
- Sample spaces, and in particular the space \(\{0,1\}^n\)
- Events, probabilities of unions and intersections.
- Random variables and their expectation, variance, and standard deviation.
- Independence and correlation for both events and random variables.
- Markov, Chebyshev and Chernoff tail bounds (bounding the probability that a random variable will deviate from its expectation).
“God doesn’t play dice with the universe”, Albert Einstein
“Einstein was doubly wrong … not only does God definitely play dice, but He sometimes confuses us by throwing them where they can’t be seen.”, Stephen Hawking
“‘The probability of winning a battle has no place in our theory because it does not belong to any [random experiment]. Probability cannot be applied to this problem any more than the physical concept of work can be applied to the ’work’ done by an actor reciting his part.”, Richard Von Mises, 1928 (paraphrased)
“I am unable to see why ‘objectivity’ requires us to interpret every probability as a frequency in some random experiment; particularly when in most problems probabilities are frequencies only in an imaginary universe invented just for the purpose of allowing a frequency interpretation.”, E.T. Jaynes, 1976
Before we show how to use randomness in algorithms, let us do a quick review of some basic notions in probability theory. This is not meant to replace a course on probability theory, and if you have not seen this material before, I highly recommend you look at additional resources to get up to speed. Fortunately, we will not need many of the advanced notions of probability theory, but, as we will see, even the so-called “simple” setting of tossing \(n\) coins can lead to very subtle and interesting issues.
This chapter contains an overview of the basics of probability theory, as needed for understanding randomized computation. The main topics covered are the notions of:
A sample space, which for us will almost always consist of the set of all possible outcomes of the experiment of tossing a finite number of independent coins.
An event, which is simply a subset of the sample space, with the probability of the event happening being the fraction of outcomes that are in this subset.
A random variable, which is a way to assign some number or statistic to an outcome of the sample space.
The notion of conditioning, which corresponds to how the value of a random variable (or the probability of an event) changes if we restrict attention to outcomes for which the value of another variable is known (or for which some other event has happened). Random variables and events that have no impact on one another are called independent.
Expectation, which is the average of a random variable, and concentration bounds which quantify the probability that a random variable can “stray too far” from its expected value.
These concepts are at once both basic and subtle. While we will not need many “fancy” topics covered in statistics courses, including special distributions (e.g., gemoetric, Poisson, exponential, Gaussian, etc.), nor topics such as hypothesis testing or regression, this doesn’t mean that the probability we use is “trivial”. The human brain has not evolved to do probabilistic reasoning very well, and notions such as conditioning and independence can be quite subtle and confusing even in the basic setting of tossing a random coin. However, this is all the more reason that studying these notions in this basic setting is useful not just for following this book, but also as a strong foundation for “fancier topics”.
Random coins
The nature of randomness and probability is a topic of great philosophical, scientific and mathematical depth. Is there actual randomness in the world, or does it proceed in a deterministic clockwork fashion from some initial conditions set at the beginning of time? Does probability refer to our uncertainty of beliefs, or to the frequency of occurrences in repeated experiments? How can we define probability over infinite sets?
These are all important questions that have been studied and debated by scientists, mathematicians, statisticians and philosophers. Fortunately, we will not need to deal directly with these questions here. We will be mostly interested in the setting of tossing \(n\) random, unbiased and independent coins. Below we define the basic probabilistic objects of events and random variables when restricted to this setting. These can be defined for much more general probabilistic experiments or sample spaces, and later on we will briefly discuss how this can be done. However, the \(n\)-coin case is sufficient for almost everything we’ll need in this course.
If instead of “heads” and “tails” we encode the sides of each coin by “zero” and “one”, we can encode the result of tossing \(n\) coins as a string in \(\{0,1\}^n\). Each particular outcome \(x\in \{0,1\}^n\) is obtained with probability \(2^{-n}\). For example, if we toss three coins, then we obtain each of the 8 outcomes \(000,001,010,011,100,101,110,111\) with probability \(2^{-3}=1/8\) (see also Figure 18.1). We can describe the experiment of tossing \(n\) coins as choosing a string \(x\) uniformly at random from \(\{0,1\}^n\), and hence we’ll use the shorthand \(x\sim \{0,1\}^n\) for \(x\) that is chosen according to this experiment.
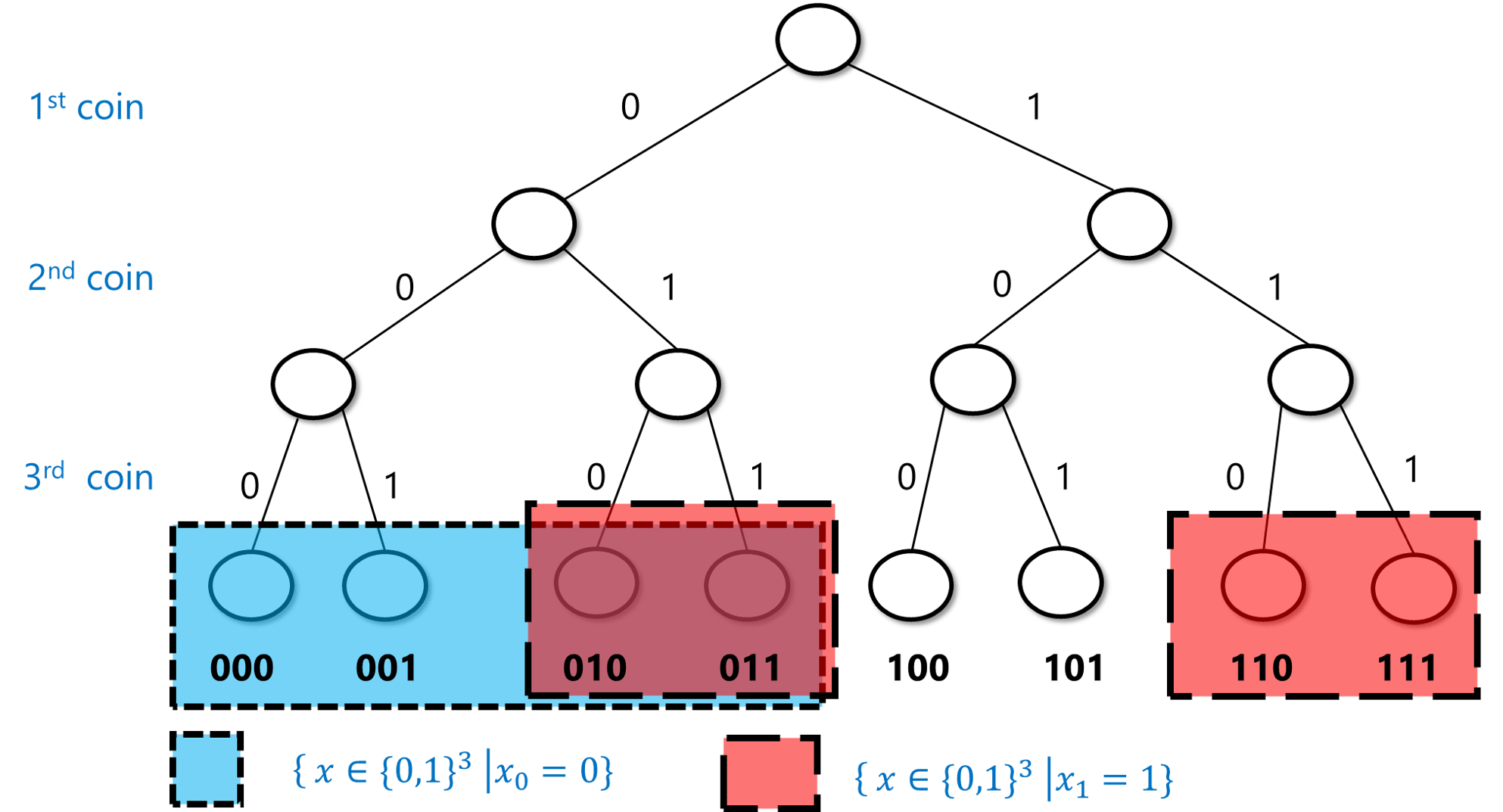
An event is simply a subset \(A\) of \(\{0,1\}^n\). The probability of \(A\), denoted by \(\Pr_{x\sim \{0,1\}^n}[A]\) (or \(\Pr[A]\) for short, when the sample space is understood from the context), is the probability that an \(x\) chosen uniformly at random will be contained in \(A\). Note that this is the same as \(|A|/2^n\) (where \(|A|\) as usual denotes the number of elements in the set \(A\)). For example, the probability that \(x\) has an even number of ones is \(\Pr[A]\) where \(A=\{ x : \sum_{i=0}^{n-1} x_i \;= 0 \mod 2 \}\). In the case \(n=3\), \(A=\{ 000,011,101,110 \}\), and hence \(\Pr[A]=\tfrac{4}{8}=\tfrac{1}{2}\) (see Figure 18.2). It turns out this is true for every \(n\):
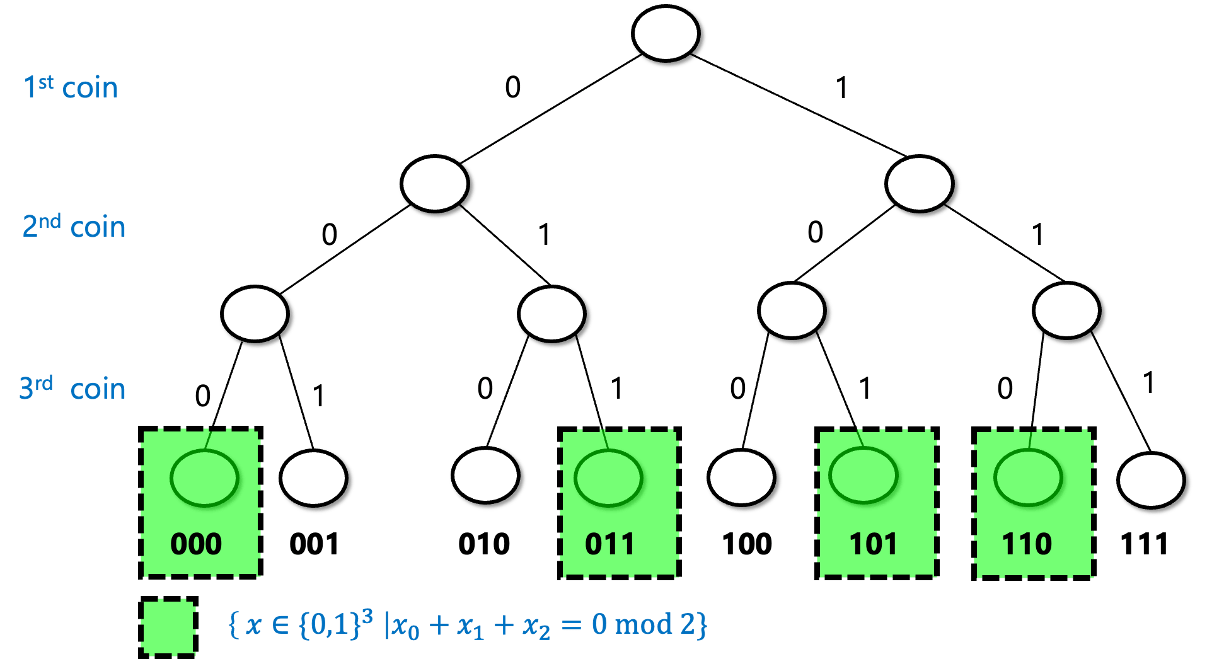
For every \(n>0\),
To test your intuition on probability, try to stop here and prove the lemma on your own.
We prove the lemma by induction on \(n\). For the case \(n=1\) it is clear since \(x=0\) is even and \(x=1\) is odd, and hence the probability that \(x\in \{0,1\}\) is even is \(1/2\). Let \(n>1\). We assume by induction that the lemma is true for \(n-1\) and we will prove it for \(n\). We split the set \(\{0,1\}^n\) into four disjoint sets \(E_0,E_1,O_0,O_1\), where for \(b\in \{0,1\}\), \(E_b\) is defined as the set of \(x\in \{0,1\}^n\) such that \(x_0\cdots x_{n-2}\) has even number of ones and \(x_{n-1}=b\) and similarly \(O_b\) is the set of \(x\in \{0,1\}^n\) such that \(x_0 \cdots x_{n-2}\) has odd number of ones and \(x_{n-1}=b\). Since \(E_0\) is obtained by simply extending \(n-1\)-length string with even number of ones by the digit \(0\), the size of \(E_0\) is simply the number of such \(n-1\)-length strings which by the induction hypothesis is \(2^{n-1}/2 = 2^{n-2}\). The same reasoning applies for \(E_1\), \(O_0\), and \(O_1\). Hence each one of the four sets \(E_0,E_1,O_0,O_1\) is of size \(2^{n-2}\). Since \(x\in \{0,1\}^n\) has an even number of ones if and only if \(x \in E_0 \cup O_1\) (i.e., either the first \(n-1\) coordinates sum up to an even number and the final coordinate is \(0\) or the first \(n-1\) coordinates sum up to an odd number and the final coordinate is \(1\)), we get that the probability that \(x\) satisfies this property is
We can also use the intersection (\(\cap\)) and union (\(\cup\)) operators to talk about the probability of both event \(A\) and event \(B\) happening, or the probability of event \(A\) or event \(B\) happening. For example, the probability \(p\) that \(x\) has an even number of ones and \(x_0=1\) is the same as \(\Pr[A\cap B]\) where \(A=\{ x\in \{0,1\}^n : \sum_{i=0}^{n-1} x_i =0 \mod 2 \}\) and \(B=\{ x\in \{0,1\}^n : x_0 = 1 \}\). This probability is equal to \(1/4\) for \(n > 1\). (It is a great exercise for you to pause here and verify that you understand why this is the case.)
Because intersection corresponds to considering the logical AND of the conditions that two events happen, while union corresponds to considering the logical OR, we will sometimes use the \(\wedge\) and \(\vee\) operators instead of \(\cap\) and \(\cup\), and so write this probability \(p=\Pr[A \cap B]\) defined above also as
If \(A \subseteq \{0,1\}^n\) is an event, then \(\overline{A} = \{0,1\}^n \setminus A\) corresponds to the event that \(A\) does not happen. Since \(|\overline{A}|=2^n-|A|\), we get that
While the above definition might seem very simple and almost trivial, the human mind seems not to have evolved for probabilistic reasoning, and it is surprising how often people can get even the simplest settings of probability wrong. One way to make sure you don’t get confused when trying to calculate probability statements is to always ask yourself the following two questions: (1) Do I understand what is the sample space that this probability is taken over?, and (2) Do I understand what is the definition of the event that we are analyzing?.
For example, suppose that I were to randomize seating in my course, and then it turned out that students sitting in row 7 performed better on the final: how surprising should we find this? If we started out with the hypothesis that there is something special about the number 7 and chose it ahead of time, then the event that we are discussing is the event \(A\) that students sitting in number 7 had better performance on the final, and we might find it surprising. However, if we first looked at the results and then chose the row whose average performance is best, then the event we are discussing is the event \(B\) that there exists some row where the performance is higher than the overall average. \(B\) is a superset of \(A\), and its probability (even if there is no correlation between sitting and performance) can be quite significant.
Random variables
Events correspond to Yes/No questions, but often we want to analyze finer questions. For example, if we make a bet at the roulette wheel, we don’t want to just analyze whether we won or lost, but also how much we’ve gained. A (real valued) random variable is simply a way to associate a number with the result of a probabilistic experiment. Formally, a random variable is a function \(X:\{0,1\}^n \rightarrow \R\) that maps every outcome \(x\in \{0,1\}^n\) to an element \(X(x) \in \R\). For example, the function \(\ensuremath{\mathit{SUM}}:\{0,1\}^n \rightarrow \R\) that maps \(x\) to the sum of its coordinates (i.e., to \(\sum_{i=0}^{n-1} x_i\)) is a random variable.
The expectation of a random variable \(X\), denoted by \(\E[X]\), is the average value that this number takes, taken over all draws from the probabilistic experiment. In other words, the expectation of \(X\) is defined as follows:
If \(X\) and \(Y\) are random variables, then we can define \(X+Y\) as simply the random variable that maps a point \(x\in \{0,1\}^n\) to \(X(x)+Y(x)\). One basic and very useful property of the expectation is that it is linear:
Similarly, \(\E[kX] = k\E[X]\) for every \(k \in \R\).
Let \(X:\{0,1\}^n \rightarrow \R\) be the random variable that maps \(x\in \{0,1\}^n\) to \(x_0 + x_1 + \ldots + x_{n-1}\). Prove that \(\E[X] = n/2\).
We can solve this using the linearity of expectation. We can define random variables \(X_0,X_1,\ldots,X_{n-1}\) such that \(X_i(x)= x_i\). Since each \(x_i\) equals \(1\) with probability \(1/2\) and \(0\) with probability \(1/2\), \(\E[X_i]=1/2\). Since \(X = \sum_{i=0}^{n-1} X_i\), by the linearity of expectation
If you have not seen discrete probability before, please go over this argument again until you are sure you follow it; it is a prototypical simple example of the type of reasoning we will employ again and again in this course.
If \(A\) is an event, then \(1_A\) is the random variable such that \(1_A(x)\) equals \(1\) if \(x\in A\), and \(1_A(x)=0\) otherwise. Note that \(\Pr[A] = \E[1_A]\) (can you see why?). Using this and the linearity of expectation, we can show one of the most useful bounds in probability theory:
For every two events \(A,B\), \(\Pr[ A \cup B] \leq \Pr[A]+\Pr[B]\)
Before looking at the proof, try to see why the union bound makes intuitive sense. We can also prove it directly from the definition of probabilities and the cardinality of sets, together with the equation \(|A \cup B| \leq |A|+|B|\). Can you see why the latter equation is true? (See also Figure 18.3.)
For every \(x\), the variable \(1_{A\cup B}(x) \leq 1_A(x)+1_B(x)\). Hence, \(\Pr[A\cup B] = \E[ 1_{A \cup B} ] \leq \E[1_A+1_B] = \E[1_A]+\E[1_B] = \Pr[A]+\Pr[B]\).
The way we often use this in theoretical computer science is to argue that, for example, if there is a list of 100 bad events that can happen, and each one of them happens with probability at most \(1/10000\), then with probability at least \(1-100/10000 = 0.99\), no bad event happens.
Distributions over strings
While most of the time we think of random variables as having as output a real number, we sometimes consider random variables whose output is a string. That is, we can think of a map \(Y:\{0,1\}^n \rightarrow \{0,1\}^*\) and consider the “random variable” \(Y\) such that for every \(y\in \{0,1\}^*\), the probability that \(Y\) outputs \(y\) is equal to \(\tfrac{1}{2^n}\left| \{ x \in \{0,1\}^n \;|\; Y(x)=y \}\right|\). To avoid confusion, we will typically refer to such string-valued random variables as distributions over strings. So, a distribution \(Y\) over strings \(\{0,1\}^*\) can be thought of as a finite collection of strings \(y_0,\ldots,y_{M-1} \in \{0,1\}^*\) and probabilities \(p_0,\ldots,p_{M-1}\) (which are non-negative numbers summing up to one), so that \(\Pr[ Y = y_i ] = p_i\).
Two distributions \(Y\) and \(Y'\) are identical if they assign the same probability to every string. For example, consider the following two functions \(Y,Y':\{0,1\}^2 \rightarrow \{0,1\}^2\). For every \(x \in \{0,1\}^2\), we define \(Y(x)=x\) and \(Y'(x)=x_0(x_0\oplus x_1)\) where \(\oplus\) is the XOR operations. Although these are two different functions, they induce the same distribution over \(\{0,1\}^2\) when invoked on a uniform input. The distribution \(Y(x)\) for \(x\sim \{0,1\}^2\) is of course the uniform distribution over \(\{0,1\}^2\). On the other hand \(Y'\) is simply the map \(00 \mapsto 00\), \(01 \mapsto 01\), \(10 \mapsto 11\), \(11 \mapsto 10\) which is a permutation of \(Y\).
More general sample spaces
While throughout most of this book we assume that the underlying probabilistic experiment corresponds to tossing \(n\) independent coins, all the claims we make easily generalize to sampling \(x\) from a more general finite or countable set \(S\) (and not-so-easily generalizes to uncountable sets \(S\) as well). A probability distribution over a finite set \(S\) is simply a function \(\mu : S \rightarrow [0,1]\) such that \(\sum_{x\in S}\mu(x)=1\). We think of this as the experiment where we obtain every \(x\in S\) with probability \(\mu(x)\), and sometimes denote this as \(x\sim \mu\). In particular, tossing \(n\) random coins corresponds to the probability distribution \(\mu:\{0,1\}^n \rightarrow [0,1]\) defined as \(\mu(x) = 2^{-n}\) for every \(x\in \{0,1\}^n\). An event \(A\) is a subset of \(S\), and the probability of \(A\), which we denote by \(\Pr_\mu[A]\), is \(\sum_{x\in A} \mu(x)\). A random variable is a function \(X:S \rightarrow \R\), where the probability that \(X=y\) is equal to \(\sum_{x\in S \text{ s.t. } X(x)=y} \mu(x)\).
Correlations and independence
One of the most delicate but important concepts in probability is the notion of independence (and the opposing notion of correlations). Subtle correlations are often behind surprises and errors in probability and statistical analysis, and several mistaken predictions have been blamed on miscalculating the correlations between, say, housing prices in Florida and Arizona, or voter preferences in Ohio and Michigan. See also Joe Blitzstein’s aptly named talk “Conditioning is the Soul of Statistics”. (Another thorny issue is of course the difference between correlation and causation. Luckily, this is another point we don’t need to worry about in our clean setting of tossing \(n\) coins.)
Two events \(A\) and \(B\) are independent if the fact that \(A\) happens makes \(B\) neither more nor less likely to happen. For example, if we think of the experiment of tossing \(3\) random coins \(x\in \{0,1\}^3\), and we let \(A\) be the event that \(x_0=1\) and \(B\) the event that \(x_0 + x_1 + x_2 \geq 2\), then if \(A\) happens it is more likely that \(B\) happens, and hence these events are not independent. On the other hand, if we let \(C\) be the event that \(x_1=1\), then because the second coin toss is not affected by the result of the first one, the events \(A\) and \(C\) are independent.
The formal definition is that events \(A\) and \(B\) are independent if \(\Pr[A \cap B]=\Pr[A] \cdot \Pr[B]\). If \(\Pr[A \cap B] > \Pr[A]\cdot \Pr[B]\) then we say that \(A\) and \(B\) are positively correlated, while if \(\Pr[ A \cap B] < \Pr[A] \cdot \Pr[B]\) then we say that \(A\) and \(B\) are negatively correlated (see Figure 18.4).
If we consider the above examples on the experiment of choosing \(x\in \{0,1\}^3\) then we can see that
but
and hence, as we already observed, the events \(\{ x_0 = 1 \}\) and \(\{ x_0+x_1+x_2 \geq 2 \}\) are not independent and in fact are positively correlated. On the other hand, \(\Pr[ x_0 = 1 \wedge x_1 = 1 ] = \Pr[ \{110,111 \}] = \tfrac{2}{8} = \tfrac{1}{2} \cdot \tfrac{1}{2}\) and hence the events \(\{x_0 = 1 \}\) and \(\{ x_1 = 1 \}\) are indeed independent.
People sometimes confuse the notion of disjointness and independence, but these are actually quite different. Two events \(A\) and \(B\) are disjoint if \(A \cap B = \emptyset\), which means that if \(A\) happens then \(B\) definitely does not happen. They are independent if \(\Pr[A \cap B]=\Pr[A]\Pr[B]\) which means that knowing that \(A\) happens gives us no information about whether \(B\) happened or not. If \(A\) and \(B\) have non-zero probability, then being disjoint implies that they are not independent, since in particular it means that they are negatively correlated.
Conditional probability: If \(A\) and \(B\) are events, and \(A\) happens with non-zero probability then we define the probability that \(B\) happens conditioned on \(A\) to be \(\Pr[B|A] = \Pr[A \cap B]/\Pr[A]\). This corresponds to calculating the probability that \(B\) happens if we already know that \(A\) happened. Note that \(A\) and \(B\) are independent if and only if \(\Pr[B|A]=\Pr[B]\).
More than two events: We can generalize this definition to more than two events. We say that events \(A_1,\ldots,A_k\) are mutually independent if knowing that any set of them occurred or didn’t occur does not change the probability that an event outside the set occurs. Formally, the condition is that for every subset \(I \subseteq [k]\),
For example, if \(x\sim \{0,1\}^3\), then the events \(\{ x_0=1 \}\), \(\{ x_1 = 1\}\) and \(\{x_2 = 1 \}\) are mutually independent. On the other hand, the events \(\{x_0 = 1 \}\), \(\{x_1 = 1\}\) and \(\{ x_0 + x_1 = 0 \mod 2 \}\) are not mutually independent, even though every pair of these events is independent (can you see why? see also Figure 18.5).
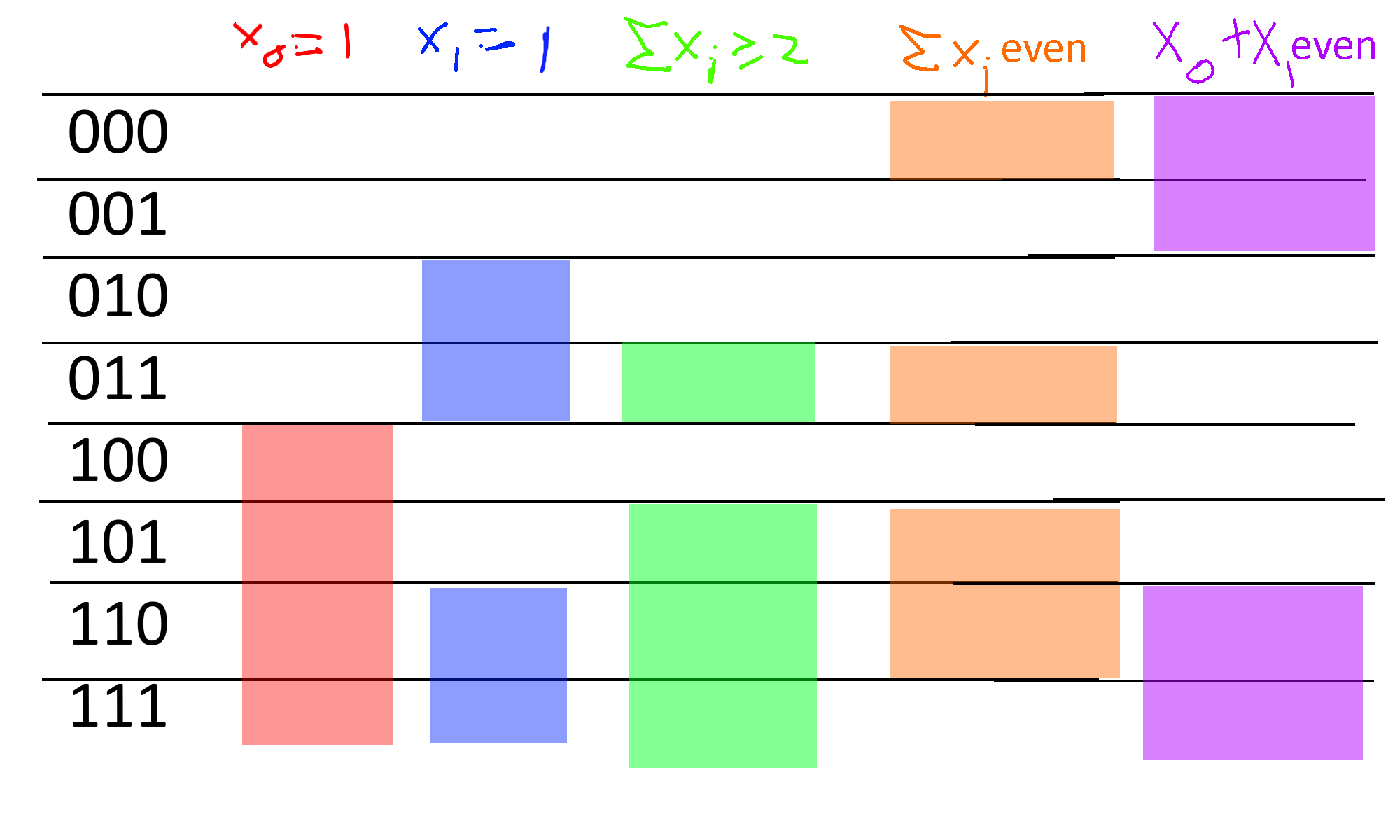
Independent random variables
We say that two random variables \(X:\{0,1\}^n \rightarrow \R\) and \(Y:\{0,1\}^n \rightarrow \R\) are independent if for every \(u,v \in \R\), the events \(\{ X=u \}\) and \(\{ Y=v \}\) are independent. (We use \(\{ X=u \}\) as shorthand for \(\{ x \;|\; X(x)=u \}\).) In other words, \(X\) and \(Y\) are independent if \(\Pr[ X=u \wedge Y=v]=\Pr[X=u]\Pr[Y=v]\) for every \(u,v \in \R\). For example, if two random variables depend on the result of tossing different coins then they are independent:
Suppose that \(S=\{ s_0,\ldots, s_{k-1} \}\) and \(T=\{ t_0 ,\ldots, t_{m-1} \}\) are disjoint subsets of \(\{0,\ldots,n-1\}\) and let \(X,Y:\{0,1\}^n \rightarrow \R\) be random variables such that \(X=F(x_{s_0},\ldots,x_{s_{k-1}})\) and \(Y=G(x_{t_0},\ldots,x_{t_{m-1}})\) for some functions \(F: \{0,1\}^k \rightarrow \R\) and \(G: \{0,1\}^m \rightarrow \R\). Then \(X\) and \(Y\) are independent.
The notation in the lemma’s statement is a bit cumbersome, but at the end of the day, it simply says that if \(X\) and \(Y\) are random variables that depend on two disjoint sets \(S\) and \(T\) of coins (for example, \(X\) might be the sum of the first \(n/2\) coins, and \(Y\) might be the largest consecutive stretch of zeroes in the second \(n/2\) coins), then they are independent.
Let \(a,b\in \R\), and let \(A = \{ x \in \{0,1\}^k : F(x)=a \}\) and \(B=\{ x\in \{0,1\}^m : G(x)=b \}\). Since \(S\) and \(T\) are disjoint, we can reorder the indices so that \(S = \{0,\ldots,k-1\}\) and \(T=\{k,\ldots,k+m-1\}\) without affecting any of the probabilities. Hence we can write \(\Pr[X=a \wedge Y=b] = |C|/2^n\) where \(C= \{ x_0,\ldots,x_{n-1} : (x_0,\ldots,x_{k-1}) \in A \wedge (x_k,\ldots,x_{k+m-1}) \in B \}\). Another way to write this using string concatenation is that \(C = \{ xyz : x\in A, y\in B, z\in \{0,1\}^{n-k-m} \}\), and hence \(|C|=|A||B|2^{n-k-m}\), which means that
If \(X\) and \(Y\) are independent random variables then (letting \(S_X,S_Y\) denote the sets of all numbers that have positive probability of being the output of \(X\) and \(Y\), respectively):
Another useful fact is that if \(X\) and \(Y\) are independent random variables, then so are \(F(X)\) and \(G(Y)\) for all functions \(F,G:\R \rightarrow \R\). This is intuitively true since learning \(F(X)\) can only provide us with less information than does learning \(X\) itself. Hence, if learning \(X\) does not teach us anything about \(Y\) (and so also about \(G(Y)\)) then neither will learning \(F(X)\). Indeed, to prove this we can write for every \(a,b \in \R\):
Collections of independent random variables
We can extend the notions of independence to more than two random variables: we say that the random variables \(X_0,\ldots,X_{n-1}\) are mutually independent if for every \(a_0,\ldots,a_{n-1} \in \R\),
If \(X_0,\ldots,X_{n-1}\) are mutually independent then
If \(X_0,\ldots,X_{n-1}\) are mutually independent, and \(Y_0,\ldots,Y_{n-1}\) are defined as \(Y_i = F_i(X_i)\) for some functions \(F_0,\ldots,F_{n-1}:\R \rightarrow \R\), then \(Y_0,\ldots,Y_{n-1}\) are mutually independent as well.
We leave proving Lemma 18.7 and Lemma 18.8 as Exercise 18.6 and Exercise 18.7. It is a good idea for you stop now and do these exercises to make sure you are comfortable with the notion of independence, as we will use it heavily later on in this course.
Concentration and tail bounds
The name “expectation” is somewhat misleading. For example, suppose that you and I place a bet on the outcome of 10 coin tosses, where if they all come out to be \(1\)’s then I pay you 100,000 dollars and otherwise you pay me 10 dollars. If we let \(X:\{0,1\}^{10} \rightarrow \R\) be the random variable denoting your gain, then we see that
But we don’t really “expect” the result of this experiment to be for you to gain 90 dollars. Rather, 99.9% of the time you will pay me 10 dollars, and you will hit the jackpot 0.1% of the times.
However, if we repeat this experiment again and again (with fresh and hence independent coins), then in the long run we do expect your average earning to be close to 90 dollars, which is the reason why casinos can make money in a predictable way even though every individual bet is random. For example, if we toss \(n\) independent and unbiased coins, then as \(n\) grows, the number of coins that come up ones will be more and more concentrated around \(n/2\) according to the famous “bell curve” (see Figure 18.6).
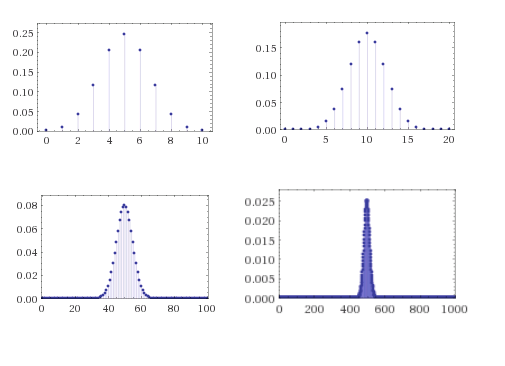
Much of probability theory is concerned with so called concentration or tail bounds, which are upper bounds on the probability that a random variable \(X\) deviates too much from its expectation. The first and simplest one of them is Markov’s inequality:
If \(X\) is a non-negative random variable then for every \(k>0\), \(\Pr[ X \geq k \E[X] ] \leq 1/k\).
Markov’s Inequality is actually a very natural statement (see also Figure 18.7). For example, if you know that the average (not the median!) household income in the US is 70,000 dollars, then in particular you can deduce that at most 25 percent of households make more than 280,000 dollars, since otherwise, even if the remaining 75 percent had zero income, the top 25 percent alone would cause the average income to be larger than 70,000 dollars. From this example you can already see that in many situations, Markov’s inequality will not be tight and the probability of deviating from expectation will be much smaller: see the Chebyshev and Chernoff inequalities below.
Let \(\mu = \E[X]\) and define \(Y=1_{X \geq k \mu}\). That is, \(Y(x)=1\) if \(X(x) \geq k \mu\) and \(Y(x)=0\) otherwise. Note that by definition, for every \(x\), \(Y(x) \leq X/(k\mu)\). We need to show \(\E[Y] \leq 1/k\). But this follows since \(\E[Y] \leq \E[X/k(\mu)] = \E[X]/(k\mu) = \mu/(k\mu)=1/k\).
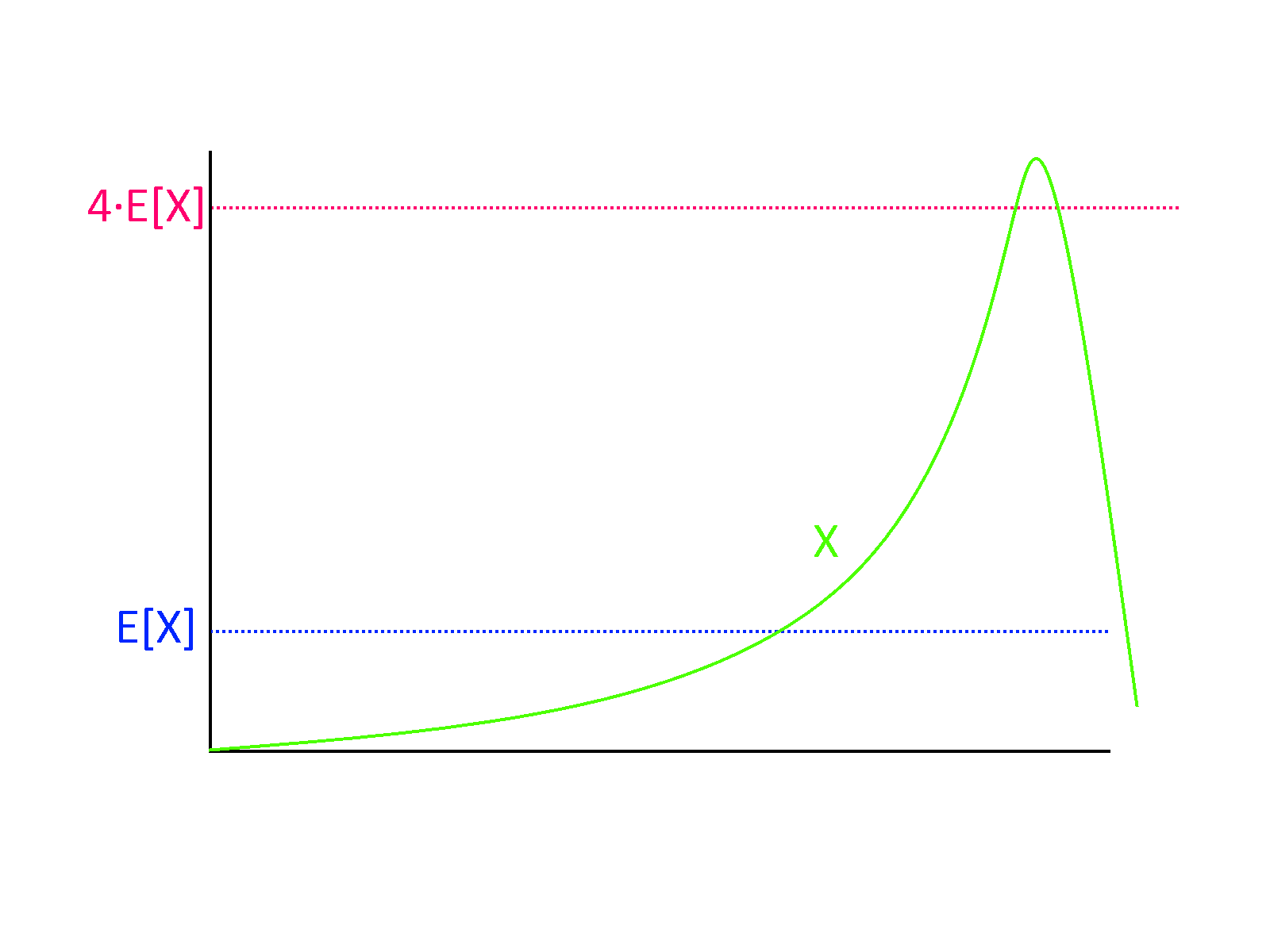
The averaging principle. While the expectation of a random variable \(X\) is hardly always the “typical value”, we can show that \(X\) is guaranteed to achieve a value that is at least its expectation with positive probability. For example, if the average grade in an exam is \(87\) points, at least one student got a grade \(87\) or more on the exam. This is known as the averaging principle, and despite its simplicity it is surprisingly useful.
Let \(X\) be a random variable, then \(\Pr[ X \geq \E[X] ] >0\).
Suppose towards the sake of contradiction that \(\Pr[ X < \E[X] ] =1\). Then the random variable \(Y = \E[X]-X\) is always positive. By linearity of expectation \(\E[Y] = \E[X] - \E[X]=0\). Yet by Markov, a non-negative random variable \(Y\) with \(\E[Y]=0\) must equal \(0\) with probability \(1\), since the probability that \(Y> k\cdot 0 = 0\) is at most \(1/k\) for every \(k>1\). Hence we get a contradiction to the assumption that \(Y\) is always positive.
Chebyshev’s Inequality
Markov’s inequality says that a (non-negative) random variable \(X\) can’t go too crazy and be, say, a million times its expectation, with significant probability. But ideally we would like to say that with high probability, \(X\) should be very close to its expectation, e.g., in the range \([0.99 \mu, 1.01 \mu]\) where \(\mu = \E[X]\). In such a case we say that \(X\) is concentrated, and hence its expectation (i.e., mean) will be close to its median and other ways of measuring \(X\)’s “typical value”. Chebyshev’s inequality can be thought of as saying that \(X\) is concentrated if it has a small standard deviation.
A standard way to measure the deviation of a random variable from its expectation is by using its standard deviation. For a random variable \(X\), we define the variance of \(X\) as \(\mathrm{Var}[X] = \E[(X-\mu)^2]\) where \(\mu = \E[X]\); i.e., the variance is the average squared distance of \(X\) from its expectation. The standard deviation of \(X\) is defined as \(\sigma[X] = \sqrt{\mathrm{Var}[X]}\). (This is well-defined since the variance, being an average of a square, is always a non-negative number.)
Using Chebyshev’s inequality, we can control the probability that a random variable is too many standard deviations away from its expectation.
Suppose that \(\mu=\E[X]\) and \(\sigma^2 = \mathrm{Var}[X]\). Then for every \(k>0\), \(\Pr[ |X-\mu | \geq k \sigma ] \leq 1/k^2\).
The proof follows from Markov’s inequality. We define the random variable \(Y = (X-\mu)^2\). Then \(\E[Y] = \mathrm{Var}[X] = \sigma^2\), and hence by Markov the probability that \(Y > k^2\sigma^2\) is at most \(1/k^2\). But clearly \((X-\mu)^2 \geq k^2\sigma^2\) if and only if \(|X-\mu| \geq k\sigma\).
One example of how to use Chebyshev’s inequality is the setting when \(X = X_1 + \cdots + X_n\) where \(X_i\)’s are independent and identically distributed (i.i.d for short) variables with values in \([0,1]\) where each has expectation \(1/2\). Since \(\E[X] = \sum_i \E[X_i] = n/2\), we would like to say that \(X\) is very likely to be in, say, the interval \([0.499n,0.501n]\). Using Markov’s inequality directly will not help us, since it will only tell us that \(X\) is very likely to be at most \(100n\) (which we already knew, since it always lies between \(0\) and \(n\)). However, since \(X_1,\ldots,X_n\) are independent, (We leave showing this to the reader as Exercise 18.8.)
For every random variable \(X_i\) in \([0,1]\), \(\mathrm{Var}[X_i] \leq 1\) (if the variable is always in \([0,1]\), it can’t be more than \(1\) away from its expectation), and hence Equation 18.1 implies that \(\mathrm{Var}[X]\leq n\) and hence \(\sigma[X] \leq \sqrt{n}\). For large \(n\), \(\sqrt{n} \ll 0.001n\), and in particular if \(\sqrt{n} \leq 0.001n/k\), we can use Chebyshev’s inequality to bound the probability that \(X\) is not in \([0.499n,0.501n]\) by \(1/k^2\).
The Chernoff bound
Chebyshev’s inequality already shows a connection between independence and concentration, but in many cases we can hope for a quantitatively much stronger result. If, as in the example above, \(X= X_1+\ldots+X_n\) where the \(X_i\)’s are bounded i.i.d random variables of mean \(1/2\), then as \(n\) grows, the distribution of \(X\) would be roughly the normal or Gaussian distribution\(-\) that is, distributed according to the bell curve (see Figure 18.6 and Figure 18.8). This distribution has the property of being very concentrated in the sense that the probability of deviating \(k\) standard deviations from the mean is not merely \(1/k^2\) as is guaranteed by Chebyshev, but rather is roughly \(e^{-k^2}\). Specifically, for a normal random variable \(X\) of expectation \(\mu\) and standard deviation \(\sigma\), the probability that \(|X-\mu| \geq k\sigma\) is at most \(2e^{-k^2/2}\). That is, we have an exponential decay of the probability of deviation.
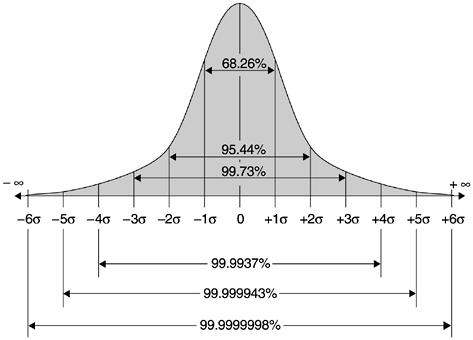
The following extremely useful theorem shows that such exponential decay occurs every time we have a sum of independent and bounded variables. This theorem is known under many names in different communities, though it is mostly called the Chernoff bound in the computer science literature:
If \(X_0,\ldots,X_{n-1}\) are i.i.d random variables such that \(X_i \in [0,1]\) and \(\E[X_i]=p\) for every \(i\), then for every \(\epsilon >0\)
We omit the proof, which appears in many texts, and uses Markov’s inequality on i.i.d random variables \(Y_0,\ldots,Y_n\) that are of the form \(Y_i = e^{\lambda X_i}\) for some carefully chosen parameter \(\lambda\). See Exercise 18.11 for a proof of the simple (but highly useful and representative) case where each \(X_i\) is \(\{0,1\}\) valued and \(p=1/2\). (See also Exercise 18.12 for a generalization.)
Since \(e\) is roughly \(2.7\) (and in particular larger than \(2\)),
Equation 18.2 would still be true if we replaced its right-hand side with \(e^{-2\epsilon^2 n + 1}\). For \(n>1/\epsilon^2\), the equation will still be true if we replaced the right-hand side with the simpler \(e^{-\epsilon^2 n}\). Hence we will sometimes use the Chernoff bound as stating that for \(X_0,\ldots,X_{n-1}\) and \(p\) as above, \(n> 1/\epsilon^2\) then
Application: Supervised learning and empirical risk minimization
Here is a nice application of the Chernoff bound. Consider the task of supervised learning. You are given a set \(S\) of \(n\) samples of the form \((x_0,y_0),\ldots,(x_{n-1},y_{n-1})\) drawn from some unknown distribution \(D\) over pairs \((x,y)\). For simplicity we will assume that \(x_i \in \{0,1\}^m\) and \(y_i \in \{0,1\}\). (We use here the concept of general distribution over the finite set \(\{0,1\}^{m+1}\) as discussed in Section 18.1.3.) The goal is to find a classifier \(h:\{0,1\}^m \rightarrow \{0,1\}\) that will minimize the test error which is the probability \(L(h)\) that \(h(x) \neq y\) where \((x,y)\) is drawn from the distribution \(D\). That is, \(L(h) = \Pr_{(x,y) \sim D}[ h(x) \neq y]\).
One way to find such a classifier is to consider a collection \(\mathcal{C}\) of potential classifiers and look at the classifier \(h\) in \(\mathcal{C}\) that does best on the training set \(S\). The classifier \(h\) is known as the empirical risk minimizer (see also Section 12.1.6) . The Chernoff bound can be used to show that as long as the number \(n\) of samples is sufficiently larger than the logarithm of \(|\mathcal{C}|\), the test error \(L(h)\) will be close to its training error \(\hat{L}_S(h)\), which is defined as the fraction of pairs \((x_i,y_i) \in S\) that it fails to classify. (Equivalently, \(\hat{L}_S(h) = \tfrac{1}{n}\sum_{i\in [n]} |h(x_i)-y_i|\).)
Let \(D\) be any distribution over pairs \((x,y) \in \{0,1\}^{m+1}\) and \(\mathcal{C}\) be any set of functions mapping \(\{0,1\}^m\) to \(\{0,1\}\). Then for every \(\epsilon, \delta>0\), if \(n > \tfrac{\log |\mathcal{C}| \log(1/\delta)}{\epsilon^2}\) and \(S\) is a set of \((x_0,y_0),\ldots,(x_{n-1},y_{n-1})\) samples that are drawn independently from \(D\) then
In particular if \(|\mathcal{C}| \leq 2^k\) and \(n> \tfrac{k\log(1/\delta)}{\epsilon^2}\) then with probability at least \(1-\delta\), the classifier \(h_* \in \mathcal{C}\) that minimizes that empirical test error \(\hat{L}_S(C)\) satisfies \(L(h_*) \leq \hat{L}_S(h_*) + \epsilon\), and hence its test error is at most \(\epsilon\) worse than its training error.
The idea is to combine the Chernoff bound with the union bound. Let \(k = \log |\mathcal{C}|\). We first use the Chernoff bound to show that for every fixed \(h \in \mathcal{C}\), if we choose \(S\) at random then the probability that \(|L(h) - \hat{L}_S(h)| > \epsilon\) will be smaller than \(\tfrac{\delta}{2^k}\). We can then use the union bound over all the \(2^k\) members of \(\mathcal{C}\) to show that this will be the case for every \(h\).
Set \(k = \log |\mathcal{C}|\) and so \(n>k \log(1/\delta)/\epsilon^2\). We start by making the following claim.
CLAIM: For every \(h\in \mathcal{C}\), the probability over \(S\) that \(|L(h)-\hat{L}_S(h)| \geq \epsilon\) is smaller than \(\delta/2^k\).
We prove the claim using the Chernoff bound. Specifically, for every such \(h\), let us define a collection of random variables \(X_0,\ldots,X_{n-1}\) as follows:
Since the samples \((x_0,y_0),\ldots,(x_{n-1},y_{n-1})\) are drawn independently from the same distribution \(D\), the random variables \(X_0,\ldots,X_{n-1}\) are independently and identically distributed. Moreover, for every \(i\), \(\E[X_i] = L(h)\). Hence by the Chernoff bound (see Equation 18.3), the probability that \(| \sum_{i=0}^{n-1} X_i - n\cdot L(h)| \geq \epsilon n\) is at most \(e^{-\epsilon^2 n} < e^{-k \log(1/\delta)} < \delta/2^k\) (using the fact that \(e>2\)). Since \(\hat{L}(h) = \tfrac{1}{n}\sum_{i\in [n]}X_i\), this completes the proof of the claim.
Given the claim, the theorem follows from the union bound. Indeed, for every \(h \in \mathcal{C}\), define the “bad event” \(B_h\) to be the event (over the choice of \(S\)) that \(|L(h) - \hat{L}_S(h)| > \epsilon\). By the claim \(\Pr[ B_h ] < \delta/2^k\), and hence by the union bound the probability that the union of \(B_h\) for all \(h\in \mathcal{H}\) happens is smaller than \(|\mathcal{C}|\delta/2^k = \delta\). If for every \(h\in\mathcal{C}\), \(B_h\) does not happen, it means that for every \(h \in\mathcal{H}\), \(|L(h) - \hat{L}_S(h)| \leq \epsilon\), and so the probability of the latter event is larger than \(1-\delta\) which is what we wanted to prove.
- A basic probabilistic experiment corresponds to tossing \(n\) coins or choosing \(x\) uniformly at random from \(\{0,1\}^n\).
- Random variables assign a real number to every result of a coin toss. The expectation of a random variable \(X\) is its average value.
- There are several concentration results, also known as tail bounds showing that under certain conditions, random variables deviate significantly from their expectation only with small probability.
Exercises
Suppose that we toss three independent fair coins \(a,b,c \in \{0,1\}\). What is the probability that the XOR of \(a\),\(b\), and \(c\) is equal to \(1\)? What is the probability that the AND of these three values is equal to \(1\)? Are these two events independent?
Give an example of random variables \(X,Y: \{0,1\}^3 \rightarrow \R\) such that \(\E[\ensuremath{\mathit{XY}}] \neq \E[X]\E[Y]\).
Give an example of random variables \(X,Y: \{0,1\}^3 \rightarrow \R\) such that \(X\) and \(Y\) are not independent but \(\E[\ensuremath{\mathit{XY}}] =\E[X]\E[Y]\).
Let \(n\) be an odd number, and let \(X:\{0,1\}^n \rightarrow \R\) be the random variable defined as follows: for every \(x\in \{0,1\}^n\), \(X(x)=1\) if \(\sum_{i=0}x_i > n/2\) and \(X(x)=0\) otherwise. Prove that \(\E[X] = 1/2\).
Give an example for a random variable \(X\) such that \(X\)’s standard deviation is equal to \({\mathbb{E}}[ | X - {\mathbb{E}}[X] | ]\).
Give an example for a random variable \(X\) such that \(X\)’s standard deviation is not equal to \({\mathbb{E}}[ | X - {\mathbb{E}}[X] | ]\).
Prove Lemma 18.7.
Prove Lemma 18.8.
Prove that if \(X_0,\ldots,X_{n-1}\) are independent random variables then \(\mathrm{Var}[X_0+\cdots+X_{n-1}]=\sum_{i=0}^{n-1} \mathrm{Var}[X_i]\).
Recall the definition of a distribution \(\mu\) over some finite set \(S\). Shannon defined the entropy of a distribution \(\mu\), denoted by \(H(\mu)\), to be \(\sum_{x\in S} \mu(x)\log(1/\mu(x))\). The idea is that if \(\mu\) is a distribution of entropy \(k\), then encoding members of \(\mu\) will require \(k\) bits, in an amortized sense. In this exercise we justify this definition. Let \(\mu\) be such that \(H(\mu)=k\).
1. Prove that for every one-to-one function \(F:S \rightarrow \{0,1\}^*\), \(\E_{x \sim \mu} |F(x)| \geq k\).
2. Prove that for every \(\epsilon\), there is some \(n\) and a one-to-one function \(F:S^n \rightarrow \{0,1\}^*\), such that \(\E_{x\sim \mu^n} |F(x)| \leq n(k+\epsilon)\), where \(x \sim \mu\) denotes the experiments of choosing \(x_0,\ldots,x_{n-1}\) each independently from \(S\) using the distribution \(\mu\).
Let \(H(p) = p \log(1/p)+(1-p)\log(1/(1-p))\).1 Prove that for every \(p \in (0,1)\) and \(\epsilon>0\), if \(n\) is large enough then2
Prove that \(\Pr_{x\sim \{0,1\}^n}[ \sum x_i = k ] = \binom{n}{k}2^{-n}\).
Use this and Exercise 18.10 to prove (an approximate version of) the Chernoff bound for the case that \(X_0,\ldots,X_{n-1}\) are i.i.d. random variables over \(\{0,1\}\) each equaling \(0\) and \(1\) with probability \(1/2\). That is, prove that for every \(\epsilon>0\), and \(X_0,\ldots,X_{n-1}\) as above, \(\Pr[ |\sum_{i=0}^{n-1} X_i - \tfrac{n}{2}| > \epsilon n] < 2^{0.1 \cdot \epsilon^2 n}\).
Exercise 18.11 establishes the Chernoff bound for the case that \(X_0,\ldots,X_{n-1}\) are i.i.d variables over \(\{0,1\}\) with expectation \(1/2\). In this exercise we use a slightly different method (bounding the moments of the random variables) to establish a version of Chernoff where the random variables range over \([0,1]\) and their expectation is some number \(p \in [0,1]\) that may be different than \(1/2\). Let \(X_0,\ldots,X_{n-1}\) be i.i.d random variables with \(\E X_i = p\) and \(\Pr [ 0 \leq X_i \leq 1 ]=1\). Define \(Y_i = X_i - p\).
Prove that for every \(j_0,\ldots,j_{n-1} \in \N\), if there exists one \(i\) such that \(j_i\) is odd then \(\E [\prod_{i=0}^{n-1} Y_i^{j_i}] = 0\).
Prove that for every \(k\), \(\E[ (\sum_{i=0}^{n-1} Y_i)^k ] \leq (10kn)^{k/2}\).3
Prove that for every \(\epsilon>0\), \(\Pr[ |\sum_i Y_i| \geq \epsilon n ] \geq 2^{-\epsilon^2 n / (10000\log 1/\epsilon)}\).4
Suppose that a country has 300,000,000 citizens, 52 percent of which prefer the color “green” and 48 percent of which prefer the color “orange”. Suppose we sample \(n\) random citizens and ask them their favorite color (assume they will answer truthfully). What is the smallest value \(n\) among the following choices so that the probability that the majority of the sample answers “green” is at most \(0.05\)?
1,000
10,000
100,000
1,000,000
Would the answer to Exercise 18.13 change if the country had 300,000,000,000 citizens?
Under the same assumptions as Exercise 18.13, what is the smallest value \(n\) among the following choices so that the probability that the majority of the sample answers “green” is at most \(2^{-100}\)?
1,000
10,000
100,000
1,000,000
It is impossible to get such low probability since there are fewer than \(2^{100}\) citizens.
Bibliographical notes
There are many sources for more information on discrete probability, including the texts referenced in Section 1.9. One particularly recommended source for probability is Harvard’s STAT 110 class, whose lectures are available on youtube and whose book is available online.
The version of the Chernoff bound that we stated in Theorem 18.12 is sometimes known as Hoeffding’s Inequality. Other variants of the Chernoff bound are known as well, but all of them are equally good for the applications of this book.
- ↩
While you don’t need this to solve this exercise, this is the function that maps \(p\) to the entropy (as defined in Exercise 18.9) of the \(p\)-biased coin distribution over \(\{0,1\}\), which is the function \(\mu:\{0,1\}\rightarrow [0,1]\) s.t. \(\mu(0)=1-p\) and \(\mu(1)=p\).
- ↩
Hint: Use Stirling’s formula for approximating the factorial function.
- ↩
Hint: Bound the number of tuples \(j_0,\ldots,j_{n-1}\) such that every \(j_i\) is even and \(\sum j_i = k\) using the Binomial coefficient and the fact that in any such tuple there are at most \(k/2\) distinct indices.
- ↩
Hint: Set \(k=2\lceil \epsilon^2 n /1000 \rceil\) and then show that if the event \(|\sum Y_i | \geq \epsilon n\) happens then the random variable \((\sum Y_i)^k\) is a factor of \(\epsilon^{-k}\) larger than its expectation.
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 12/06/2023 00:06:53
Copyright 2023, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.