See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
Syntactic sugar, and computing every function
- Get comfortable with syntactic sugar or automatic translation of higher-level logic to low-level gates.
- Learn proof of major result: every finite function can be computed by a Boolean circuit.
- Start thinking quantitatively about the number of lines required for computation.
“[In 1951] I had a running compiler and nobody would touch it because, they carefully told me, computers could only do arithmetic; they could not do programs.”, Grace Murray Hopper, 1986.
“Syntactic sugar causes cancer of the semicolon.”, Alan Perlis, 1982.
The computational models we considered thus far are as “bare bones” as they come. For example, our NAND-CIRC “programming language” has only the single operation foo = NAND(bar,blah). In this chapter we will see that these simple models are actually equivalent to more sophisticated ones. The key observation is that we can implement more complex features using our basic building blocks, and then use these new features themselves as building blocks for even more sophisticated features. This is known as “syntactic sugar” in the field of programming language design since we are not modifying the underlying programming model itself, but rather we merely implement new features by syntactically transforming a program that uses such features into one that doesn’t.
This chapter provides a “toolkit” that can be used to show that many functions can be computed by NAND-CIRC programs, and hence also by Boolean circuits. We will also use this toolkit to prove a fundamental theorem: every finite function \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) can be computed by a Boolean circuit, see Theorem 4.13 below. While the syntactic sugar toolkit is important in its own right, Theorem 4.13 can also be proven directly without using this toolkit. We present this alternative proof in Section 4.5. See Figure 4.1 for an outline of the results of this chapter.
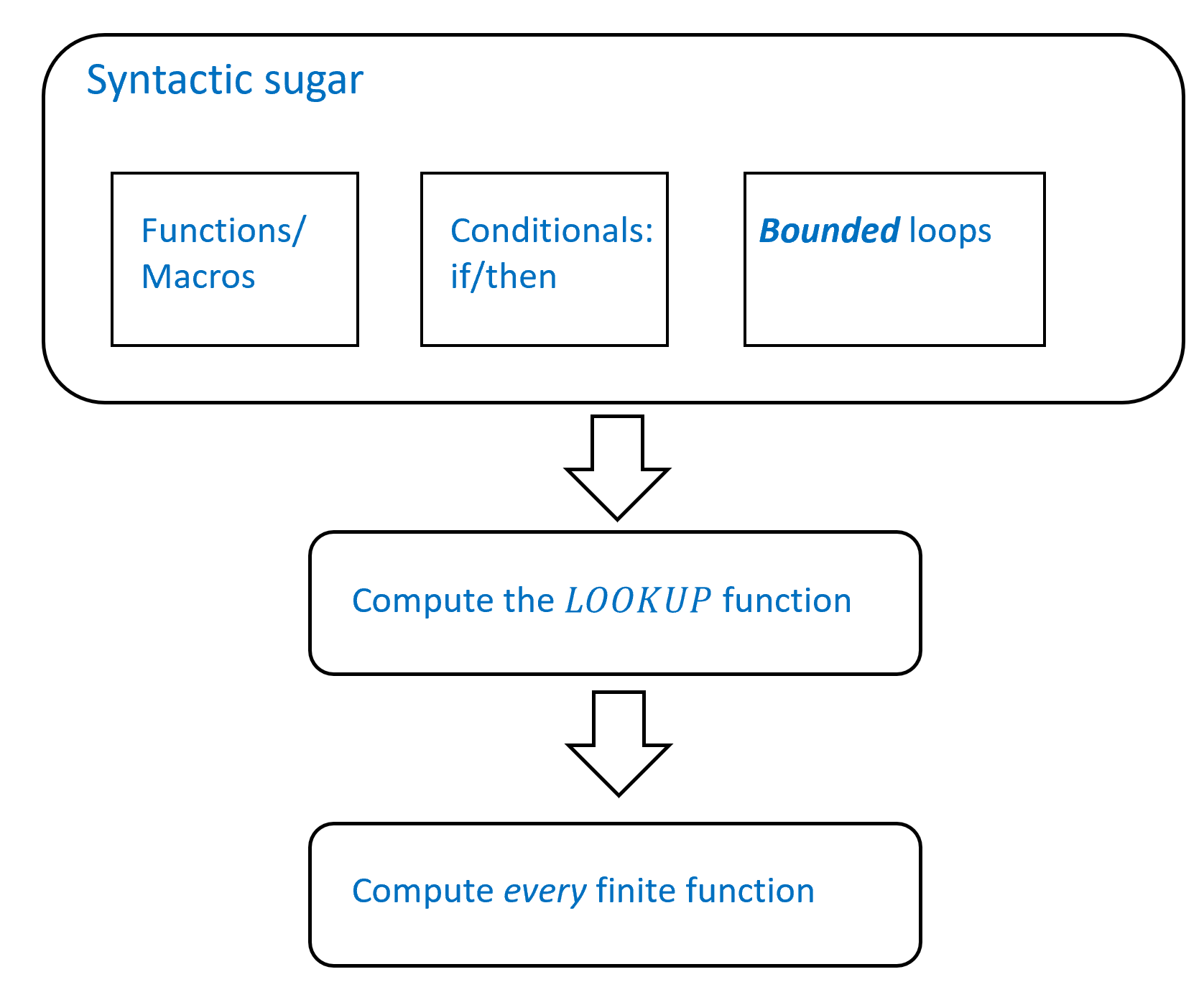
In this chapter, we will see our first major result: every finite function can be computed by some Boolean circuit (see Theorem 4.13 and Big Idea 5). This is sometimes known as the “universality” of \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\) (and, using the equivalence of Chapter 3, of \(\ensuremath{\mathit{NAND}}\) as well)
Despite being an important result, Theorem 4.13 is actually not that hard to prove. Section 4.5 presents a relatively simple direct proof of this result. However, in Section 4.1 and Section 4.3 we derive this result using the concept of “syntactic sugar” (see Big Idea 4). This is an important concept for programming languages theory and practice. The idea behind “syntactic sugar” is that we can extend a programming language by implementing advanced features from its basic components. For example, we can take the AON-CIRC and NAND-CIRC programming languages we saw in Chapter 3, and extend them to achieve features such as user-defined functions (e.g., def Foo(...)), conditional statements (e.g., if blah ...), and more. Once we have these features, it is not that hard to show that we can take the “truth table” (table of all inputs and outputs) of any function, and use that to create an AON-CIRC or NAND-CIRC program that maps each input to its corresponding output.
We will also get our first glimpse of quantitative measures in this chapter. While Theorem 4.13 tells us that every function can be computed by some circuit, the number of gates in this circuit can be exponentially large. (We are not using here “exponentially” as some colloquial term for “very very big” but in a very precise mathematical sense, which also happens to coincide with being very very big.) It turns out that some functions (for example, integer addition and multiplication) can be in fact computed using far fewer gates. We will explore this issue of “gate complexity” more deeply in Chapter 5 and following chapters.
Some examples of syntactic sugar
We now present some examples of “syntactic sugar” transformations that we can use in constructing straightline programs or circuits. We focus on the straight-line programming language view of our computational models, and specifically (for the sake of concreteness) on the NAND-CIRC programming language. This is convenient because many of the syntactic sugar transformations we present are easiest to think about in terms of applying “search and replace” operations to the source code of a program. However, by Theorem 3.19, all of our results hold equally well for circuits, whether ones using NAND gates or Boolean circuits that use the AND, OR, and NOT operations. Enumerating the examples of such syntactic sugar transformations can be a little tedious, but we do it for two reasons:
To convince you that despite their seeming simplicity and limitations, simple models such as Boolean circuits or the NAND-CIRC programming language are actually quite powerful.
So you can realize how lucky you are to be taking a theory of computation course and not a compilers course…
:)
User-defined procedures
One staple of almost any programming language is the ability to define and then execute procedures or subroutines. (These are often known as functions in some programming languages, but we prefer the name procedures to avoid confusion with the function that a program computes.) The NAND-CIRC programming language does not have this mechanism built in. However, we can achieve the same effect using the time-honored technique of “copy and paste”. Specifically, we can replace code which defines a procedure such as
with the following code where we “paste” the code of Proc
and where proc_code' is obtained by replacing all occurrences of a with d, b with e, and c with f. When doing that we will need to ensure that all other variables appearing in proc_code' don’t interfere with other variables. We can always do so by renaming variables to new names that were not used before. The above reasoning leads to the proof of the following theorem:
Let NAND-CIRC-PROC be the programming language NAND-CIRC augmented with the syntax above for defining procedures. Then for every NAND-CIRC-PROC program \(P\), there exists a standard (i.e., “sugar-free”) NAND-CIRC program \(P'\) that computes the same function as \(P\).
NAND-CIRC-PROC only allows non-recursive procedures. In particular, the code of a procedure Proc cannot call Proc but only use procedures that were defined before it. Without this restriction, the above “search and replace” procedure might never terminate and Theorem 4.1 would not be true.
Theorem 4.1 can be proven using the transformation above, but since the formal proof is somewhat long and tedious, we omit it here.
Procedures allow us to express NAND-CIRC programs much more cleanly and succinctly. For example, because we can compute AND, OR, and NOT using NANDs, we can compute the Majority function as follows:
def NOT(a):
return NAND(a,a)
def AND(a,b):
temp = NAND(a,b)
return NOT(temp)
def OR(a,b):
temp1 = NOT(a)
temp2 = NOT(b)
return NAND(temp1,temp2)
def MAJ(a,b,c):
and1 = AND(a,b)
and2 = AND(a,c)
and3 = AND(b,c)
or1 = OR(and1,and2)
return OR(or1,and3)
print(MAJ(0,1,1))
# 1Figure 4.2 presents the “sugar-free” NAND-CIRC program (and the corresponding circuit) that is obtained by “expanding out” this program, replacing the calls to procedures with their definitions.
Once we show that a computational model \(X\) is equivalent to a model that has feature \(Y\), we can assume we have \(Y\) when showing that a function \(f\) is computable by \(X\).
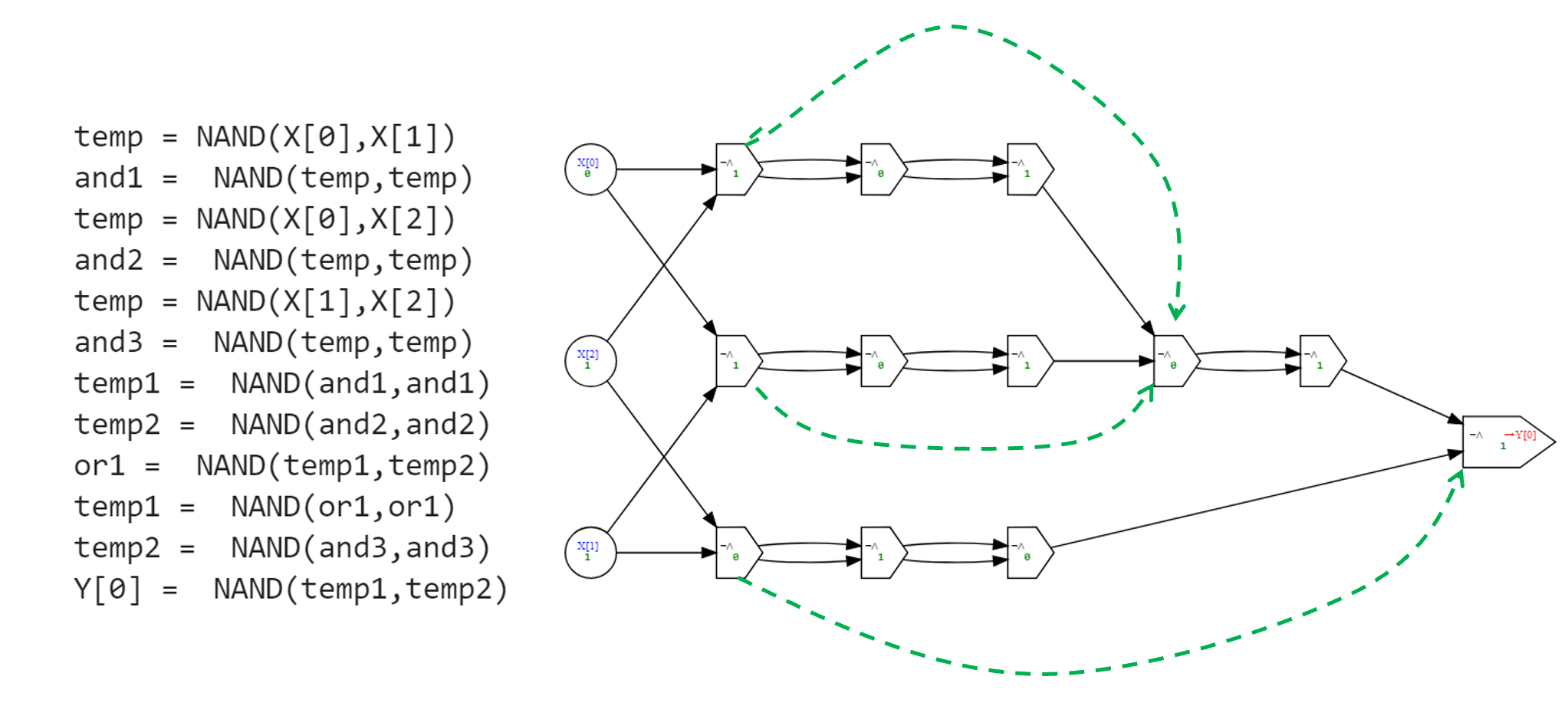
While we can use syntactic sugar to present NAND-CIRC programs in more readable ways, we did not change the definition of the language itself. Therefore, whenever we say that some function \(f\) has an \(s\)-line NAND-CIRC program we mean a standard “sugar-free” NAND-CIRC program, where all syntactic sugar has been expanded out. For example, the program of Example 4.3 is a \(12\)-line program for computing the \(\ensuremath{\mathit{MAJ}}\) function, even though it can be written in fewer lines using NAND-CIRC-PROC.
Proof by Python (optional)
We can write a Python program that implements the proof of Theorem 4.1. This is a Python program that takes a NAND-CIRC-PROC program \(P\) that includes procedure definitions and uses simple “search and replace” to transform \(P\) into a standard (i.e., “sugar-free”) NAND-CIRC program \(P'\) that computes the same function as \(P\) without using any procedures. The idea is simple: if the program \(P\) contains a definition of a procedure Proc of two arguments x and y, then whenever we see a line of the form foo = Proc(bar,blah), we can replace this line by:
The body of the procedure
Proc(replacing all occurrences ofxandywithbarandblahrespectively).A line
foo = exp, whereexpis the expression following thereturnstatement in the definition of the procedureProc.
To make this more robust we add a prefix to the internal variables used by Proc to ensure they don’t conflict with the variables of \(P\); for simplicity we ignore this issue in the code below though it can be easily added.
The code of the Python function desugar below achieves such a transformation.
Figure 4.3: Python code for transforming NAND-CIRC-PROC programs into standard sugar-free NAND-CIRC programs.
def desugar(code, func_name, func_args,func_body):
"""
Replaces all occurences of
foo = func_name(func_args)
with
func_body[x->a,y->b]
foo = [result returned in func_body]
"""
# Uses Python regular expressions to simplify the search and replace,
# see https://docs.python.org/3/library/re.html and Chapter 9 of the book
# regular expression for capturing a list of variable names separated by commas
arglist = ",".join([r"([a-zA-Z0-9\_\[\]]+)" for i in range(len(func_args))])
# regular expression for capturing a statement of the form
# "variable = func_name(arguments)"
regexp = fr'([a-zA-Z0-9\_\[\]]+)\s*=\s*{func_name}\({arglist}\)\s*$'
while True:
m = re.search(regexp, code, re.MULTILINE)
if not m: break
newcode = func_body
# replace function arguments by the variables from the function invocation
for i in range(len(func_args)):
newcode = newcode.replace(func_args[i], m.group(i+2))
# Splice the new code inside
newcode = newcode.replace('return', m.group(1) + " = ")
code = code[:m.start()] + newcode + code[m.end()+1:]
return codeFigure 4.2 shows the result of applying desugar to the program of Example 4.3 that uses syntactic sugar to compute the Majority function. Specifically, we first apply desugar to remove usage of the OR function, then apply it to remove usage of the AND function, and finally apply it a third time to remove usage of the NOT function.
The function desugar in Figure 4.3 assumes that it is given the procedure already split up into its name, arguments, and body. It is not crucial for our purposes to describe precisely how to scan a definition and split it up into these components, but in case you are curious, it can be achieved in Python via the following code:
Conditional statements
Another sorely missing feature in NAND-CIRC is a conditional statement such as the if/then constructs that are found in many programming languages. However, using procedures, we can obtain an ersatz if/then construct. First we can compute the function \(\ensuremath{\mathit{IF}}:\{0,1\}^3 \rightarrow \{0,1\}\) such that \(\ensuremath{\mathit{IF}}(a,b,c)\) equals \(b\) if \(a=1\) and \(c\) if \(a=0\).
Before reading onward, try to see how you could compute the \(\ensuremath{\mathit{IF}}\) function using \(\ensuremath{\mathit{NAND}}\)’s. Once you do that, see how you can use that to emulate if/then types of constructs.
The \(\ensuremath{\mathit{IF}}\) function can be implemented from NANDs as follows (see Exercise 4.2):
def IF(cond,a,b):
notcond = NAND(cond,cond)
temp = NAND(b,notcond)
temp1 = NAND(a,cond)
return NAND(temp,temp1)The \(\ensuremath{\mathit{IF}}\) function is also known as a multiplexing function, since \(cond\) can be thought of as a switch that controls whether the output is connected to \(a\) or \(b\). Once we have a procedure for computing the \(\ensuremath{\mathit{IF}}\) function, we can implement conditionals in NAND. The idea is that we replace code of the form
with code of the form
that assigns to foo its old value when condition equals \(0\), and assign to foo the value of blah otherwise. More generally we can replace code of the form
with code of the form
temp_a = ...
temp_b = ...
temp_c = ...
a = IF(cond,temp_a,a)
b = IF(cond,temp_b,b)
c = IF(cond,temp_c,c)Using such transformations, we can prove the following theorem. Once again we omit the (not too insightful) full formal proof, though see Section 4.1.2 for some hints on how to obtain it.
Let NAND-CIRC-IF be the programming language NAND-CIRC augmented with if/then/else statements for allowing code to be conditionally executed based on whether a variable is equal to \(0\) or \(1\).
Then for every NAND-CIRC-IF program \(P\), there exists a standard (i.e., “sugar-free”) NAND-CIRC program \(P'\) that computes the same function as \(P\).
Extended example: Addition and Multiplication (optional)
Using “syntactic sugar”, we can write the integer addition function as follows:
# Add two n-bit integers
# Use LSB first notation for simplicity
def ADD(A,B):
Result = [0]*(n+1)
Carry = [0]*(n+1)
Carry[0] = zero(A[0])
for i in range(n):
Result[i] = XOR(Carry[i],XOR(A[i],B[i]))
Carry[i+1] = MAJ(Carry[i],A[i],B[i])
Result[n] = Carry[n]
return Result
ADD([1,1,1,0,0],[1,0,0,0,0]);;
# [0, 0, 0, 1, 0, 0]where zero is the constant zero function, and MAJ and XOR correspond to the majority and XOR functions respectively. While we use Python syntax for convenience, in this example \(n\) is some fixed integer and so for every such \(n\), ADD is a finite function that takes as input \(2n\) bits and outputs \(n+1\) bits. In particular for every \(n\) we can remove the loop construct for i in range(n) by simply repeating the code \(n\) times, replacing the value of i with \(0,1,2,\ldots,n-1\). By expanding out all the features, for every value of \(n\) we can translate the above program into a standard (“sugar-free”) NAND-CIRC program. Figure 4.4 depicts what we get for \(n=2\).
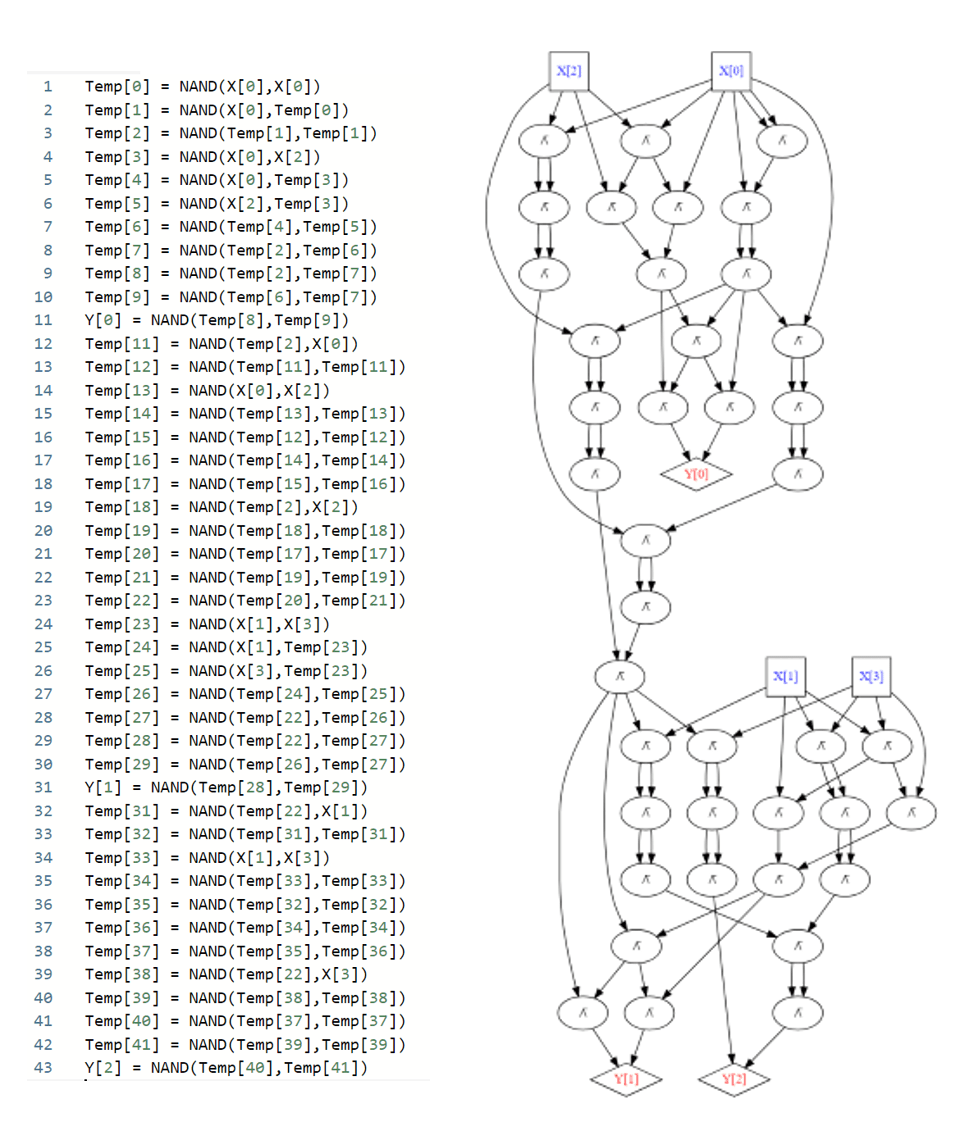
By going through the above program carefully and accounting for the number of gates, we can see that it yields a proof of the following theorem (see also Figure 4.5):
For every \(n\in \N\), let \(\ensuremath{\mathit{ADD}}_n:\{0,1\}^{2n}\rightarrow \{0,1\}^{n+1}\) be the function that, given \(x,x'\in \{0,1\}^n\) computes the representation of the sum of the numbers that \(x\) and \(x'\) represent. Then there is a constant \(c \leq 30\) such that for every \(n\) there is a NAND-CIRC program of at most \(cn\) lines computing \(\ensuremath{\mathit{ADD}}_n\).1
Once we have addition, we can use the grade-school algorithm to obtain multiplication as well, thus obtaining the following theorem:
For every \(n\), let \(\ensuremath{\mathit{MULT}}_n:\{0,1\}^{2n}\rightarrow \{0,1\}^{2n}\) be the function that, given \(x,x'\in \{0,1\}^n\) computes the representation of the product of the numbers that \(x\) and \(x'\) represent. Then there is a constant \(c\) such that for every \(n\), there is a NAND-CIRC program of at most \(cn^2\) lines that computes the function \(\ensuremath{\mathit{MULT}}_n\).
We omit the proof, though in Exercise 4.7 we ask you to supply a “constructive proof” in the form of a program (in your favorite programming language) that on input a number \(n\), outputs the code of a NAND-CIRC program of at most \(1000n^2\) lines that computes the \(\ensuremath{\mathit{MULT}}_n\) function. In fact, we can use Karatsuba’s algorithm to show that there is a NAND-CIRC program of \(O(n^{\log_2 3})\) lines to compute \(\ensuremath{\mathit{MULT}}_n\) (and can get even further asymptotic improvements using better algorithms).
The LOOKUP function
The \(\ensuremath{\mathit{LOOKUP}}\) function will play an important role in this chapter and later. It is defined as follows:
For every \(k\), the lookup function of order \(k\), \(\ensuremath{\mathit{LOOKUP}}_k: \{0,1\}^{2^k+k}\rightarrow \{0,1\}\) is defined as follows: For every \(x\in\{0,1\}^{2^k}\) and \(i\in \{0,1\}^k\),
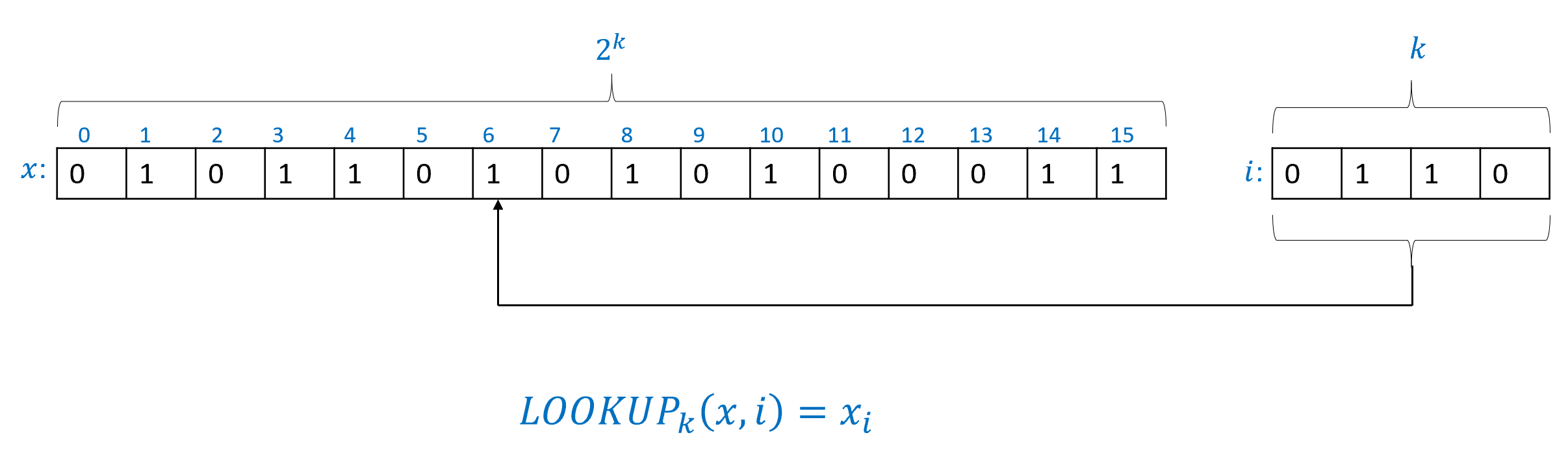
See Figure 4.6 for an illustration of the LOOKUP function. It turns out that for every \(k\), we can compute \(\ensuremath{\mathit{LOOKUP}}_k\) using a NAND-CIRC program:
For every \(k>0\), there is a NAND-CIRC program that computes the function \(\ensuremath{\mathit{LOOKUP}}_k: \{0,1\}^{2^k+k}\rightarrow \{0,1\}\). Moreover, the number of lines in this program is at most \(4\cdot 2^k\).
An immediate corollary of Theorem 4.10 is that for every \(k>0\), \(\ensuremath{\mathit{LOOKUP}}_k\) can be computed by a Boolean circuit (with AND, OR and NOT gates) of at most \(8 \cdot 2^k\) gates.
Constructing a NAND-CIRC program for \(\ensuremath{\mathit{LOOKUP}}\)
We prove Theorem 4.10 by induction. For the case \(k=1\), \(\ensuremath{\mathit{LOOKUP}}_1\) maps \((x_0,x_1,i) \in \{0,1\}^3\) to \(x_i\). In other words, if \(i=0\) then it outputs \(x_0\) and otherwise it outputs \(x_1\), which (up to reordering variables) is the same as the \(\ensuremath{\mathit{IF}}\) function presented in Section 4.1.3, which can be computed by a 4-line NAND-CIRC program.
As a warm-up for the case of general \(k\), let us consider the case of \(k=2\). Given input \(x=(x_0,x_1,x_2,x_3)\) for \(\ensuremath{\mathit{LOOKUP}}_2\) and an index \(i=(i_0,i_1)\), if the most significant bit \(i_0\) of the index is \(0\) then \(\ensuremath{\mathit{LOOKUP}}_2(x,i)\) will equal \(x_0\) if \(i_1=0\) and equal \(x_1\) if \(i_1=1\). Similarly, if the most significant bit \(i_0\) is \(1\) then \(\ensuremath{\mathit{LOOKUP}}_2(x,i)\) will equal \(x_2\) if \(i_1=0\) and will equal \(x_3\) if \(i_1=1\). Another way to say this is that we can write \(\ensuremath{\mathit{LOOKUP}}_2\) as follows:
def LOOKUP2(X[0],X[1],X[2],X[3],i[0],i[1]):
if i[0]==1:
return LOOKUP1(X[2],X[3],i[1])
else:
return LOOKUP1(X[0],X[1],i[1])or in other words,
def LOOKUP2(X[0],X[1],X[2],X[3],i[0],i[1]):
a = LOOKUP1(X[2],X[3],i[1])
b = LOOKUP1(X[0],X[1],i[1])
return IF( i[0],a,b)More generally, as shown in the following lemma, we can compute \(\ensuremath{\mathit{LOOKUP}}_k\) using two invocations of \(\ensuremath{\mathit{LOOKUP}}_{k-1}\) and one invocation of \(\ensuremath{\mathit{IF}}\):
For every \(k \geq 2\), \(\ensuremath{\mathit{LOOKUP}}_k(x_0,\ldots,x_{2^k-1},i_0,\ldots,i_{k-1})\) is equal to
If the most significant bit \(i_{0}\) of \(i\) is zero, then the index \(i\) is in \(\{0,\ldots,2^{k-1}-1\}\) and hence we can perform the lookup on the “first half” of \(x\) and the result of \(\ensuremath{\mathit{LOOKUP}}_k(x,i)\) will be the same as \(a=\ensuremath{\mathit{LOOKUP}}_{k-1}(x_0,\ldots,x_{2^{k-1}-1},i_1,\ldots,i_{k-1})\). On the other hand, if this most significant bit \(i_{0}\) is equal to \(1\), then the index is in \(\{2^{k-1},\ldots,2^k-1\}\), in which case the result of \(\ensuremath{\mathit{LOOKUP}}_k(x,i)\) is the same as \(b=\ensuremath{\mathit{LOOKUP}}_{k-1}(x_{2^{k-1}},\ldots,x_{2^k-1},i_1,\ldots,i_{k-1})\). Thus we can compute \(\ensuremath{\mathit{LOOKUP}}_k(x,i)\) by first computing \(a\) and \(b\) and then outputting \(\ensuremath{\mathit{IF}}(i_0,b,a)\).
Proof of Theorem 4.10 from Lemma 4.11. Now that we have Lemma 4.11, we can complete the proof of Theorem 4.10. We will prove by induction on \(k\) that there is a NAND-CIRC program of at most \(4\cdot (2^k-1)\) lines for \(\ensuremath{\mathit{LOOKUP}}_k\). For \(k=1\) this follows by the four line program for \(\ensuremath{\mathit{IF}}\) we’ve seen before. For \(k>1\), we use the following pseudocode:
a = LOOKUP_(k-1)(X[0],...,X[2^(k-1)-1],i[1],...,i[k-1])
b = LOOKUP_(k-1)(X[2^(k-1)],...,X[2^(k-1)],i[1],...,i[k-1])
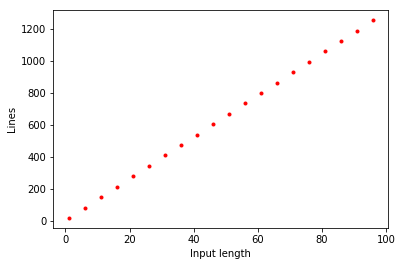
return IF(i[0],b,a)If we let \(L(k)\) be the number of lines required for \(\ensuremath{\mathit{LOOKUP}}_k\), then the above pseudo-code shows that Since under our induction hypothesis \(L(k-1) \leq 4(2^{k-1}-1)\), we get that \(L(k) \leq 2\cdot 4 (2^{k-1}-1) + 4 = 4(2^k - 1)\) which is what we wanted to prove. See Figure 4.7 for a plot of the actual number of lines in our implementation of \(\ensuremath{\mathit{LOOKUP}}_k\).
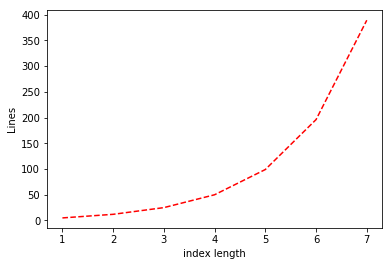
LOOKUP_k function as a function of \(k\) (i.e., the length of the index). The number of lines in our implementation is roughly \(3 \cdot 2^k\).Computing every function
At this point we know the following facts about NAND-CIRC programs (and so equivalently about Boolean circuits and our other equivalent models):
They can compute at least some non-trivial functions.
Coming up with NAND-CIRC programs for various functions is a very tedious task.
Thus I would not blame the reader if they were not particularly looking forward to a long sequence of examples of functions that can be computed by NAND-CIRC programs. However, it turns out we are not going to need this, as we can show in one fell swoop that NAND-CIRC programs can compute every finite function:
There exists some constant \(c>0\) such that for every \(n,m>0\) and function \(f: \{0,1\}^n\rightarrow \{0,1\}^m\), there is a NAND-CIRC program with at most \(c \cdot m 2^n\) lines that computes the function \(f\) .
By Theorem 3.19, the models of NAND circuits, NAND-CIRC programs, AON-CIRC programs, and Boolean circuits, are all equivalent to one another, and hence Theorem 4.12 holds for all these models. In particular, the following theorem is equivalent to Theorem 4.12:
There exists some constant \(c>0\) such that for every \(n,m>0\) and function \(f: \{0,1\}^n\rightarrow \{0,1\}^m\), there is a Boolean circuit with at most \(c \cdot m 2^n\) gates that computes the function \(f\) .
Every finite function can be computed by a large enough Boolean circuit.
Improved bounds. Though it will not be of great importance to us, it is possible to improve on the proof of Theorem 4.12 and shave an extra factor of \(n\), as well as optimize the constant \(c\), and so prove that for every \(\epsilon>0\), \(m\in \N\) and sufficiently large \(n\), if \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) then \(f\) can be computed by a NAND circuit of at most \((1+\epsilon)\tfrac{m\cdot 2^n}{n}\) gates. The proof of this result is beyond the scope of this book, but we do discuss how to obtain a bound of the form \(O(\tfrac{m \cdot 2^n}{n})\) in Section 4.4.2; see also the biographical notes.
Proof of NAND’s Universality
To prove Theorem 4.12, we need to give a NAND circuit, or equivalently a NAND-CIRC program, for every possible function. We will restrict our attention to the case of Boolean functions (i.e., \(m=1\)). Exercise 4.9 asks you to extend the proof for all values of \(m\). A function \(F: \{0,1\}^n\rightarrow \{0,1\}\) can be specified by a table of its values for each one of the \(2^n\) inputs. For example, the table below describes one particular function \(G: \{0,1\}^4 \rightarrow \{0,1\}\):2
| Input (\(x\)) | Output (\(G(x)\)) |
|---|---|
| \(0000\) | 1 |
| \(0001\) | 1 |
| \(0010\) | 0 |
| \(0011\) | 0 |
| \(0100\) | 1 |
| \(0101\) | 0 |
| \(0110\) | 0 |
| \(0111\) | 1 |
| \(1000\) | 0 |
| \(1001\) | 0 |
| \(1010\) | 0 |
| \(1011\) | 0 |
| \(1100\) | 1 |
| \(1101\) | 1 |
| \(1110\) | 1 |
| \(1111\) | 1 |
For every \(x\in \{0,1\}^4\), \(G(x)=\ensuremath{\mathit{LOOKUP}}_4(1100100100001111,x)\), and so the following is NAND-CIRC “pseudocode” to compute \(G\) using syntactic sugar for the LOOKUP_4 procedure.
G0000 = 1
G1000 = 1
G0100 = 0
...
G0111 = 1
G1111 = 1
Y[0] = LOOKUP_4(G0000,G1000,...,G1111,
X[0],X[1],X[2],X[3])We can translate this pseudocode into an actual NAND-CIRC program by adding three lines to define variables zero and one that are initialized to \(0\) and \(1\) respectively, and then replacing a statement such as Gxxx = 0 with Gxxx = NAND(one,one) and a statement such as Gxxx = 1 with Gxxx = NAND(zero,zero). The call to LOOKUP_4 will be replaced by the NAND-CIRC program that computes \(\ensuremath{\mathit{LOOKUP}}_4\), plugging in the appropriate inputs.
There was nothing about the above reasoning that was particular to the function \(G\) above. Given every function \(F: \{0,1\}^n \rightarrow \{0,1\}\), we can write a NAND-CIRC program that does the following:
Initialize \(2^n\) variables of the form
F00...0tillF11...1so that for every \(z\in\{0,1\}^n\), the variable corresponding to \(z\) is assigned the value \(F(z)\).Compute \(\ensuremath{\mathit{LOOKUP}}_n\) on the \(2^n\) variables initialized in the previous step, with the index variable being the input variables
X[\(0\)],…,X[\(n-1\)]. That is, just like in the pseudocode forGabove, we useY[0] = LOOKUP(F00..00,...,F11..1,X[0],..,X[\(n-1\)])
The total number of lines in the resulting program is \(3+2^n\) lines for initializing the variables plus the \(4\cdot 2^n\) lines that we pay for computing \(\ensuremath{\mathit{LOOKUP}}_n\). This completes the proof of Theorem 4.12.
While Theorem 4.12 seems striking at first, in retrospect, it is perhaps not that surprising that every finite function can be computed with a NAND-CIRC program. After all, a finite function \(F: \{0,1\}^n \rightarrow \{0,1\}^m\) can be represented by simply the list of its outputs for each one of the \(2^n\) input values. So it makes sense that we could write a NAND-CIRC program of similar size to compute it. What is more interesting is that some functions, such as addition and multiplication, have a much more efficient representation: one that only requires \(O(n^2)\) or even fewer lines.
Improving by a factor of \(n\) (optional)
By being a little more careful, we can improve the bound of Theorem 4.12 and show that every function \(F:\{0,1\}^n \rightarrow \{0,1\}^m\) can be computed by a NAND-CIRC program of at most \(O(m 2^n/n)\) lines. In other words, we can prove the following improved version:
There exists a constant \(c>0\) such that for every \(n,m>0\) and function \(f: \{0,1\}^n\rightarrow \{0,1\}^m\), there is a NAND-CIRC program with at most \(c \cdot m 2^n / n\) lines that computes the function \(f\).3
As before, it is enough to prove the case that \(m=1\). Hence we let \(f:\{0,1\}^n \rightarrow \{0,1\}\), and our goal is to prove that there exists a NAND-CIRC program of \(O(2^n/n)\) lines (or equivalently a Boolean circuit of \(O(2^n/n)\) gates) that computes \(f\).
We let \(k= \log(n-2\log n)\) (the reasoning behind this choice will become clear later on). We define the function \(g:\{0,1\}^k \rightarrow \{0,1\}^{2^{n-k}}\) as follows:
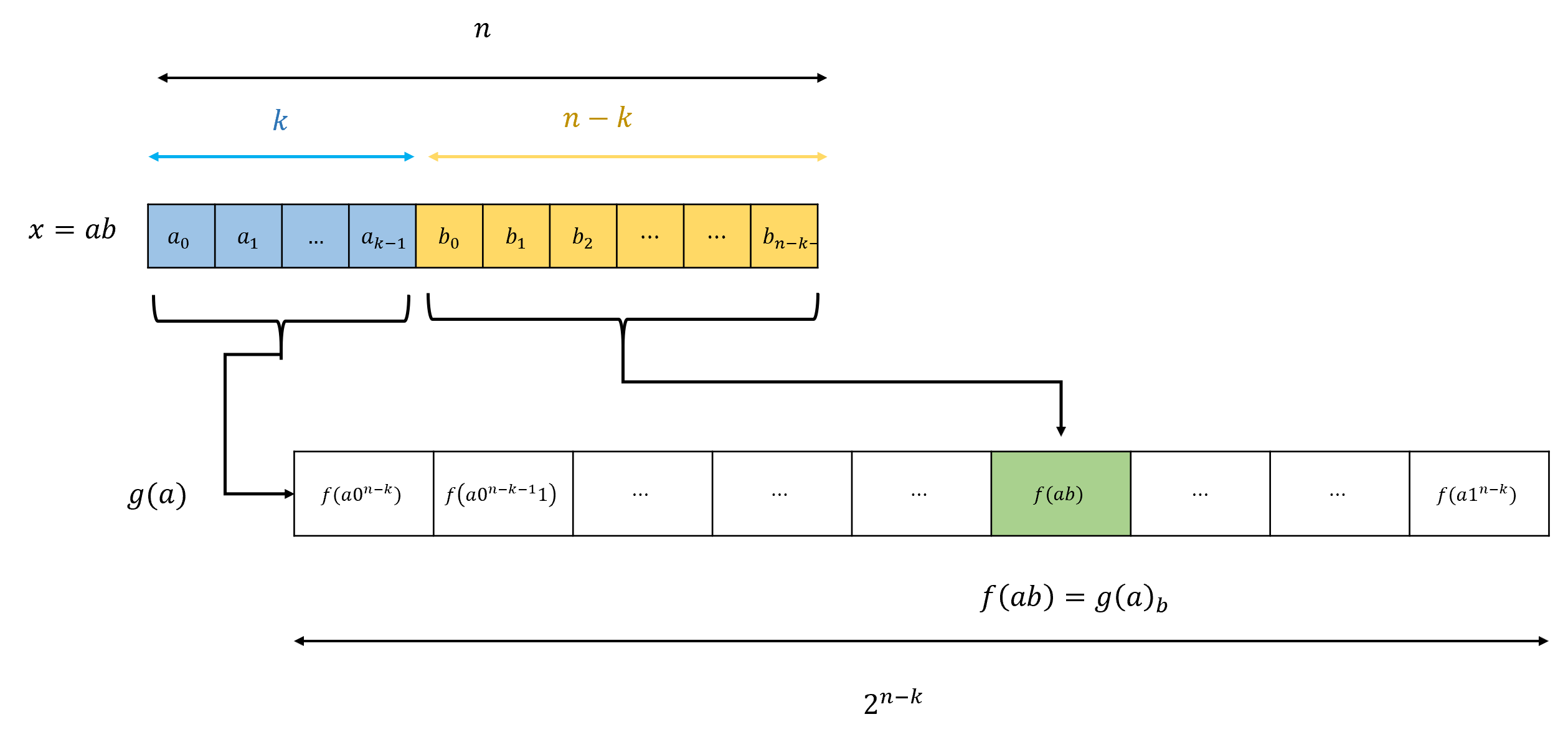
Equation 4.2 means that for every \(x\in \{0,1\}^n\), if we write \(x=ab\) with \(a\in \{0,1\}^k\) and \(b\in \{0,1\}^{n-k}\) then we can compute \(f(x)\) by first computing the string \(T=g(a)\) of length \(2^{n-k}\), and then computing \(\ensuremath{\mathit{LOOKUP}}_{n-k}(T\;,\; b)\) to retrieve the element of \(T\) at the position corresponding to \(b\) (see Figure 4.8). The cost to compute the \(\ensuremath{\mathit{LOOKUP}}_{n-k}\) is \(O(2^{n-k})\) lines/gates and the cost in NAND-CIRC lines (or Boolean gates) to compute \(f\) is at most where \(cost(g)\) is the number of operations (i.e., lines of NAND-CIRC programs or gates in a circuit) needed to compute \(g\).
To complete the proof we need to give a bound on \(cost(g)\). Since \(g\) is a function mapping \(\{0,1\}^k\) to \(\{0,1\}^{2^{n-k}}\), we can also think of it as a collection of \(2^{n-k}\) functions \(g_0,\ldots, g_{2^{n-k}-1}: \{0,1\}^k \rightarrow \{0,1\}\), where \(g_i(x) = g(a)_i\) for every \(a\in \{0,1\}^k\) and \(i\in [2^{n-k}]\). (That is, \(g_i(a)\) is the \(i\)-th bit of \(g(a)\).) Naively, we could use Theorem 4.12 to compute each \(g_i\) in \(O(2^k)\) lines, but then the total cost is \(O(2^{n-k} \cdot 2^k) = O(2^n)\) which does not save us anything. However, the crucial observation is that there are only \(2^{2^k}\) distinct functions mapping \(\{0,1\}^k\) to \(\{0,1\}\). For example, if \(g_{17}\) is an identical function to \(g_{67}\) that means that if we already computed \(g_{17}(a)\) then we can compute \(g_{67}(a)\) using only a constant number of operations: simply copy the same value! In general, if you have a collection of \(N\) functions \(g_0,\ldots,g_{N-1}\) mapping \(\{0,1\}^k\) to \(\{0,1\}\), of which at most \(S\) are distinct then for every value \(a\in \{0,1\}^k\) we can compute the \(N\) values \(g_0(a),\ldots,g_{N-1}(a)\) using at most \(O(S\cdot 2^k + N)\) operations (see Figure 4.9).
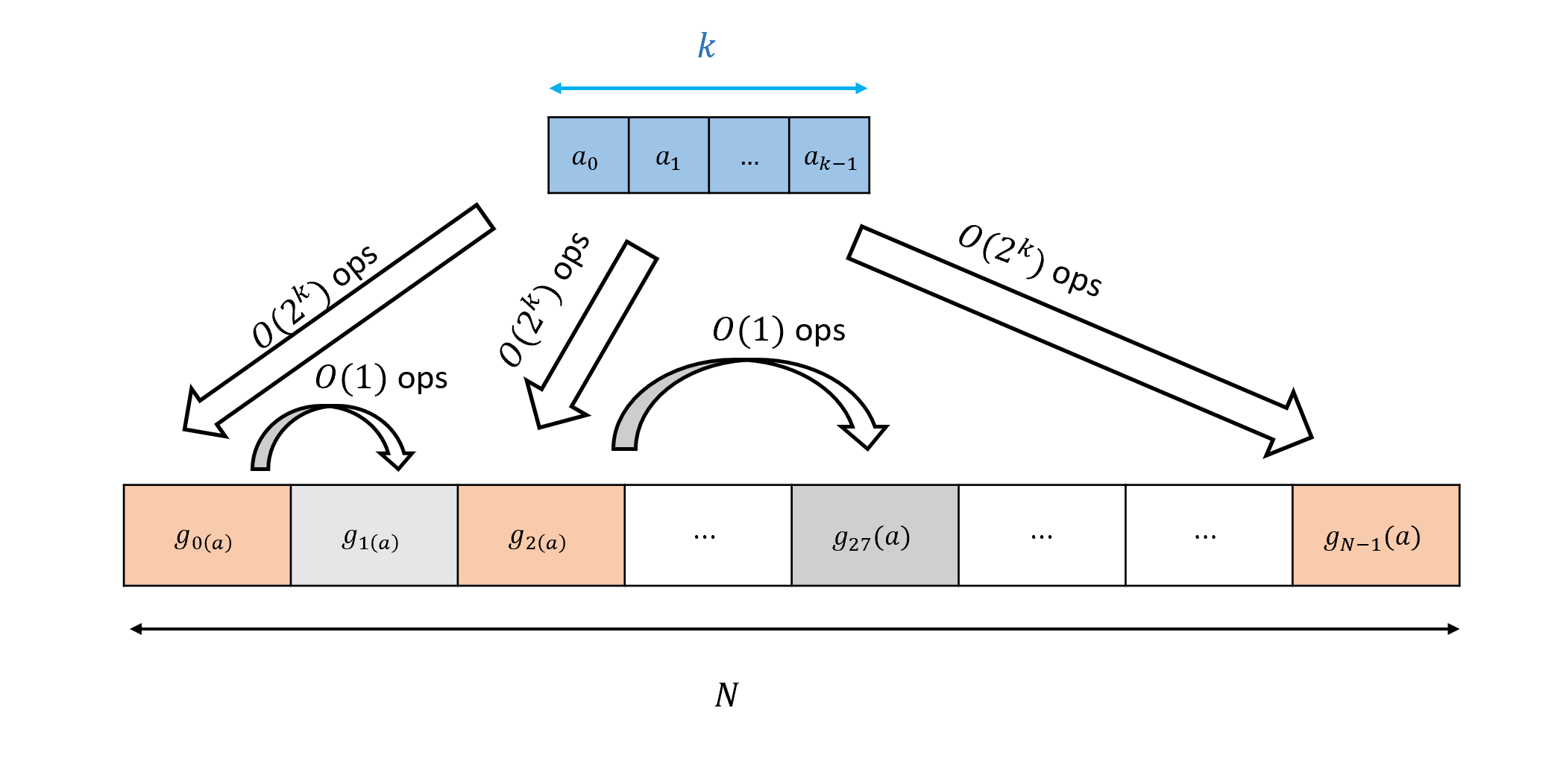
In our case, because there are at most \(2^{2^k}\) distinct functions mapping \(\{0,1\}^k\) to \(\{0,1\}\), we can compute the function \(g\) (and hence by Equation 4.2 also \(f\)) using at most
operations. Now all that is left is to plug into Equation 4.4 our choice of \(k = \log (n-2\log n)\). By definition, \(2^k = n-2\log n\), which means that Equation 4.4 can be bounded
Using the connection between NAND-CIRC programs and Boolean circuits, an immediate corollary of Theorem 4.15 is the following improvement to Theorem 4.13:
There exists some constant \(c>0\) such that for every \(n,m>0\) and function \(f: \{0,1\}^n\rightarrow \{0,1\}^m\), there is a Boolean circuit with at most \(c \cdot m 2^n / n\) gates that computes the function \(f\) .
Computing every function: An alternative proof
Theorem 4.13 is a fundamental result in the theory (and practice!) of computation. In this section, we present an alternative proof of this basic fact that Boolean circuits can compute every finite function. This alternative proof gives a somewhat worse quantitative bound on the number of gates but it has the advantage of being simpler, working directly with circuits and avoiding the usage of all the syntactic sugar machinery. (However, that machinery is useful in its own right, and will find other applications later on.)
There exists some constant \(c>0\) such that for every \(n,m>0\) and function \(f: \{0,1\}^n\rightarrow \{0,1\}^m\), there is a Boolean circuit with at most \(c \cdot m\cdot n 2^n\) gates that computes the function \(f\) .
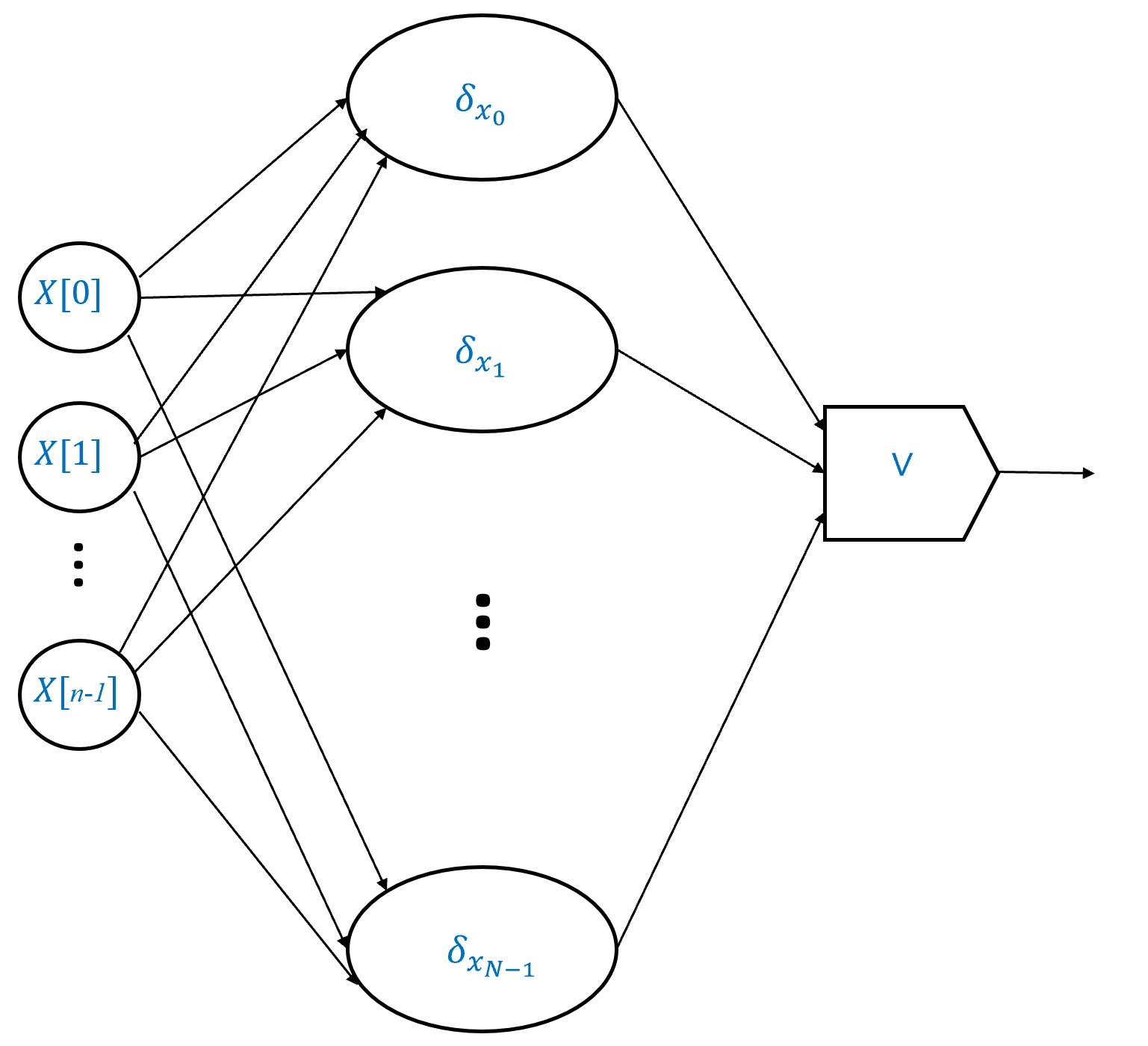
The idea of the proof is illustrated in Figure 4.10. As before, it is enough to focus on the case that \(m=1\) (the function \(f\) has a single output), since we can always extend this to the case of \(m>1\) by looking at the composition of \(m\) circuits each computing a different output bit of the function \(f\). We start by showing that for every \(\alpha \in \{0,1\}^n\), there is an \(O(n)\)-sized circuit that computes the function \(\delta_\alpha:\{0,1\}^n \rightarrow \{0,1\}\) defined as follows: \(\delta_\alpha(x)=1\) iff \(x=\alpha\) (that is, \(\delta_\alpha\) outputs \(0\) on all inputs except the input \(\alpha\)). We can then write any function \(f:\{0,1\}^n \rightarrow \{0,1\}\) as the OR of at most \(2^n\) functions \(\delta_\alpha\) for the \(\alpha\)’s on which \(f(\alpha)=1\).
We prove the theorem for the case \(m=1\). The result can be extended for \(m>1\) as before (see also Exercise 4.9). Let \(f:\{0,1\}^n \rightarrow \{0,1\}\). We will prove that there is an \(O(n\cdot 2^n)\)-sized Boolean circuit to compute \(f\) in the following steps:
We show that for every \(\alpha\in \{0,1\}^n\), there is an \(O(n)\)-sized circuit that computes the function \(\delta_\alpha:\{0,1\}^n \rightarrow \{0,1\}\), where \(\delta_\alpha(x)=1\) iff \(x=\alpha\).
We then show that this implies the existence of an \(O(n\cdot 2^n)\)-sized circuit that computes \(f\), by writing \(f(x)\) as the OR of \(\delta_\alpha(x)\) for all \(\alpha\in \{0,1\}^n\) such that \(f(\alpha)=1\). (If \(f\) is the constant zero function and hence there is no such \(\alpha\), then we can use the circuit \(f(x) = x_0 \wedge \overline{x}_0\).)
We start with Step 1:
CLAIM: For \(\alpha \in \{0,1\}^n\), define \(\delta_\alpha:\{0,1\}^n\) as follows:
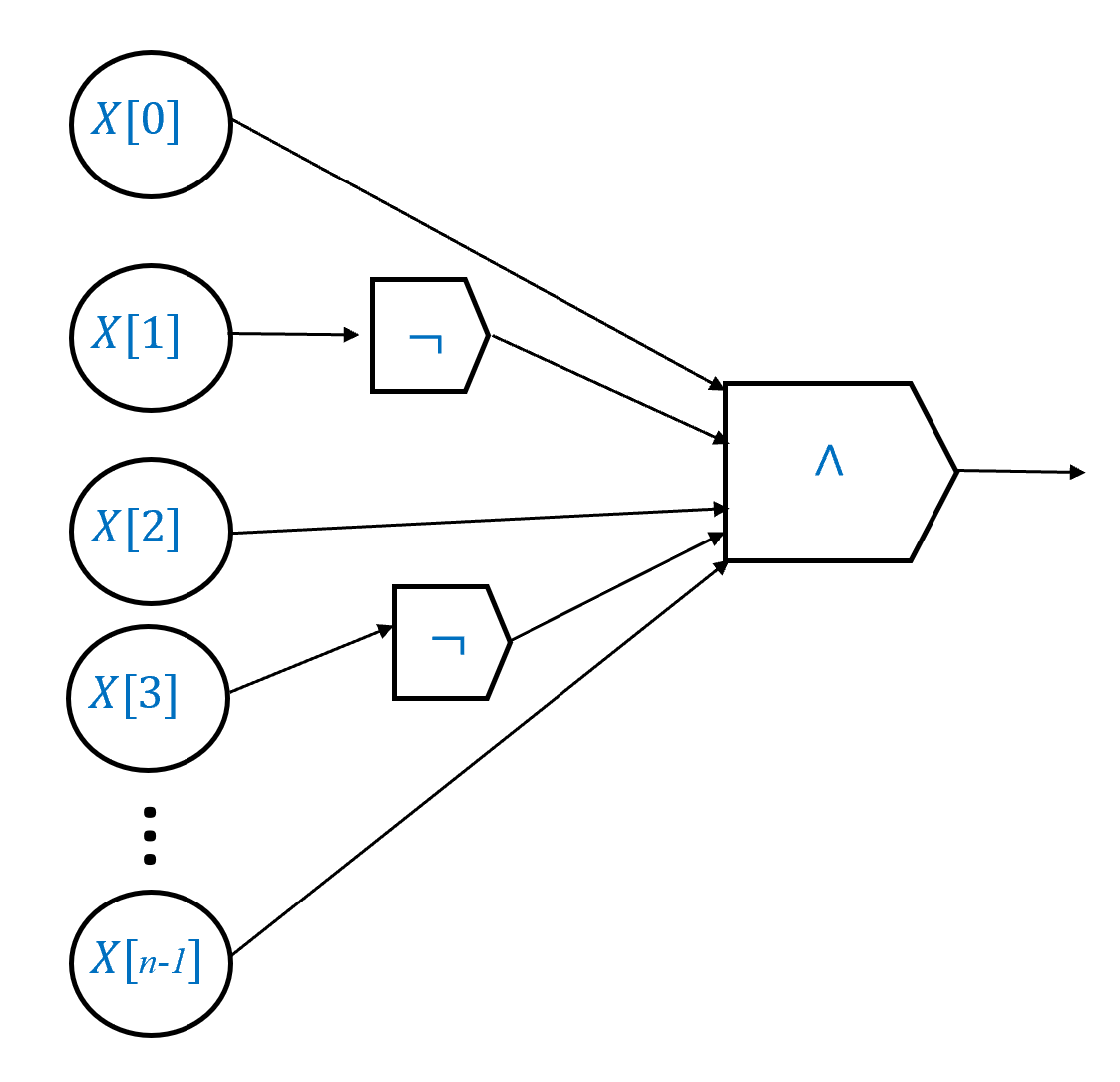
PROOF OF CLAIM: The proof is illustrated in Figure 4.11. As an example, consider the function \(\delta_{011}:\{0,1\}^3 \rightarrow \{0,1\}\). This function outputs \(1\) on \(x\) if and only if \(x_0=0\), \(x_1=1\) and \(x_2=1\), and so we can write \(\delta_{011}(x) = \overline{x_0} \wedge x_1 \wedge x_2\), which translates into a Boolean circuit with one NOT gate and two AND gates. More generally, for every \(\alpha \in \{0,1\}^n\), we can express \(\delta_{\alpha}(x)\) as \((x_0 = \alpha_0) \wedge (x_1 = \alpha_1) \wedge \cdots \wedge (x_{n-1} = \alpha_{n-1})\), where if \(\alpha_i=0\) we replace \(x_i = \alpha_i\) with \(\overline{x_i}\) and if \(\alpha_i=1\) we replace \(x_i=\alpha_i\) by simply \(x_i\). This yields a circuit that computes \(\delta_\alpha\) using \(n\) AND gates and at most \(n\) NOT gates, so a total of at most \(2n\) gates.
Now for every function \(f:\{0,1\}^n \rightarrow \{0,1\}\), we can write
where \(S=\{ x_0 ,\ldots, x_{N-1}\}\) is the set of inputs on which \(f\) outputs \(1\). (To see this, you can verify that the right-hand side of Equation 4.5 evaluates to \(1\) on \(x\in \{0,1\}^n\) if and only if \(x\) is in the set \(S\).)
Therefore we can compute \(f\) using a Boolean circuit of at most \(2n\) gates for each of the \(N\) functions \(\delta_{x_i}\) and combine that with at most \(N\) OR gates, thus obtaining a circuit of at most \(2n\cdot N + N\) gates. Since \(S \subseteq \{0,1\}^n\), its size \(N\) is at most \(2^n\) and hence the total number of gates in this circuit is \(O(n\cdot 2^n)\).
The class \(\ensuremath{\mathit{SIZE}}_{n,m}(s)\)
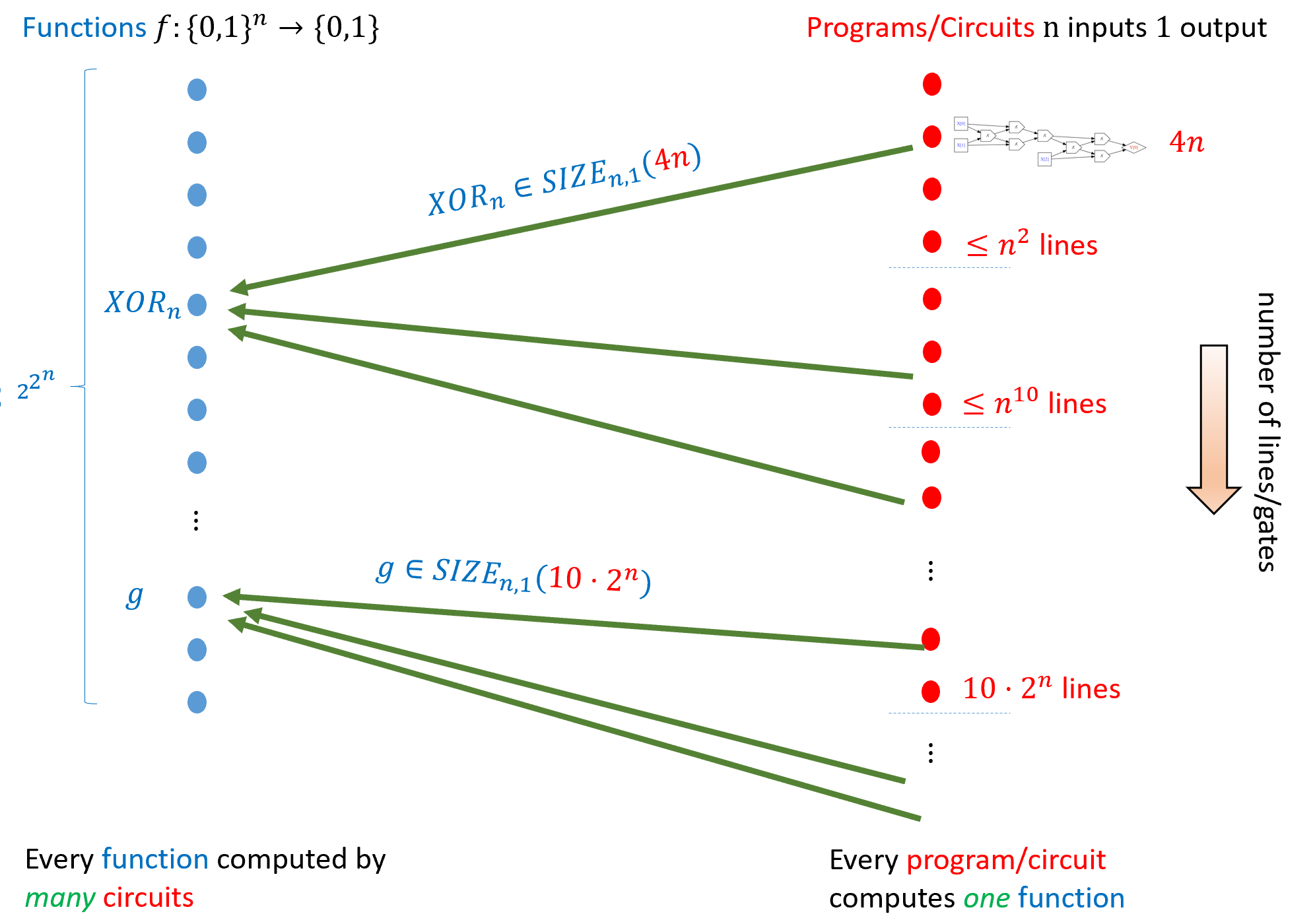
We have seen that every function \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) can be computed by a circuit of size \(O(m\cdot 2^n)\), and some functions (such as addition and multiplication) can be computed by much smaller circuits. We define \(\ensuremath{\mathit{SIZE}}_{n,m}(s)\) to be the set of functions mapping \(n\) bits to \(m\) bits that can be computed by NAND circuits of at most \(s\) gates (or equivalently, by NAND-CIRC programs of at most \(s\) lines). Formally, the definition is as follows:
For all natural numbers \(n,m,s\), let \(\ensuremath{\mathit{SIZE}}_{n,m}(s)\) denote the set of all functions \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) such that there exists a NAND circuit of at most \(s\) gates computing \(f\). We denote by \(\ensuremath{\mathit{SIZE}}_n(s)\) the set \(\ensuremath{\mathit{SIZE}}_{n,1}(s)\). For every integer \(s \geq 1\), we let \(\ensuremath{\mathit{SIZE}}(s) = \cup_{n,m} \ensuremath{\mathit{SIZE}}_{n,m}(s)\) be the set of all functions \(f\) for which there exists a NAND circuit of at most \(s\) gates that compute \(f\).
Figure 4.12 depicts the set \(\ensuremath{\mathit{SIZE}}_{n,1}(s)\). Note that \(\ensuremath{\mathit{SIZE}}_{n,m}(s)\) is a set of functions, not of programs! Asking if a program or a circuit is a member of \(\ensuremath{\mathit{SIZE}}_{n,m}(s)\) is a category error as in the sense of Figure 4.13. As we discussed in Section 3.7.2 (and Section 2.6.1), the distinction between programs and functions is absolutely crucial. You should always remember that while a program computes a function, it is not equal to a function. In particular, as we’ve seen, there can be more than one program to compute the same function.
While we defined \(\ensuremath{\mathit{SIZE}}_n(s)\) with respect to NAND gates, we would get essentially the same class if we defined it with respect to AND/OR/NOT gates:
Let \(\ensuremath{\mathit{SIZE}}^{AON}_{n,m}(s)\) denote the set of all functions \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) that can be computed by an AND/OR/NOT Boolean circuit of at most \(s\) gates. Then,
If \(f\) can be computed by a NAND circuit of at most \(s/2\) gates, then by replacing each NAND with the two gates NOT and AND, we can obtain an AND/OR/NOT Boolean circuit of at most \(s\) gates that computes \(f\). On the other hand, if \(f\) can be computed by a Boolean AND/OR/NOT circuit of at most \(s\) gates, then by Theorem 3.12 it can be computed by a NAND circuit of at most \(3s\) gates.

The results we have seen in this chapter can be phrased as showing that \(\ensuremath{\mathit{ADD}}_n \in \ensuremath{\mathit{SIZE}}_{2n,n+1}(100 n)\) and \(\ensuremath{\mathit{MULT}}_n \in \ensuremath{\mathit{SIZE}}_{2n,2n}(10000 n^{\log_2 3})\). Theorem 4.12 shows that for some constant \(c\), \(\ensuremath{\mathit{SIZE}}_{n,m}(c m 2^n)\) is equal to the set of all functions from \(\{0,1\}^n\) to \(\{0,1\}^m\).
Unlike programming languages such as Python, C or JavaScript, the NAND-CIRC and AON-CIRC programming language do not have arrays. A NAND-CIRC program \(P\) has some fixed number \(n\) and \(m\) of inputs and output variable. Hence, for example, there is no single NAND-CIRC program that can compute the increment function \(\ensuremath{\mathit{INC}}:\{0,1\}^* \rightarrow \{0,1\}^*\) that maps a string \(x\) (which we identify with a number via the binary representation) to the string that represents \(x+1\). Rather for every \(n>0\), there is a NAND-CIRC program \(P_n\) that computes the restriction \(\ensuremath{\mathit{INC}}_n\) of the function \(\ensuremath{\mathit{INC}}\) to inputs of length \(n\). Since it can be shown that for every \(n>0\) such a program \(P_n\) exists of length at most \(10n\), \(\ensuremath{\mathit{INC}}_n \in \ensuremath{\mathit{SIZE}}_{n,n+1}(10n)\) for every \(n>0\).
For the time being, our focus will be on finite functions, but we will discuss how to extend the definition of size complexity to functions with unbounded input lengths later on in Section 13.6.
In this exercise we prove a certain “closure property” of the class \(\ensuremath{\mathit{SIZE}}_n(s)\). That is, we show that if \(f\) is in this class then (up to some small additive term) so is the complement of \(f\), which is the function \(g(x)=1-f(x)\).
Prove that there is a constant \(c\) such that for every \(f:\{0,1\}^n \rightarrow \{0,1\}\) and \(s\in \N\), if \(f \in \ensuremath{\mathit{SIZE}}_n(s)\) then \(1-f \in \ensuremath{\mathit{SIZE}}_n(s+c)\).
If \(f\in \ensuremath{\mathit{SIZE}}_n(s)\) then there is an \(s\)-line NAND-CIRC program \(P\) that computes \(f\). We can rename the variable Y[0] in \(P\) to a variable temp and add the line
at the very end to obtain a program \(P'\) that computes \(1-f\).
- We can define the notion of computing a function via a simplified “programming language”, where computing a function \(F\) in \(T\) steps would correspond to having a \(T\)-line NAND-CIRC program that computes \(F\).
- While the NAND-CIRC programming only has one operation, other operations such as functions and conditional execution can be implemented using it.
- Every function \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) can be computed by a circuit of at most \(O(m 2^n)\) gates (and in fact at most \(O(m 2^n/n)\) gates).
- Sometimes (or maybe always?) we can translate an efficient algorithm to compute \(f\) into a circuit that computes \(f\) with a number of gates comparable to the number of steps in this algorithm.
Exercises
This exercise asks you to give a one-to-one map from \(\N^2\) to \(\N\). This can be useful to implement two-dimensional arrays as “syntactic sugar” in programming languages that only have one-dimensional arrays.
Prove that the map \(F(x,y)=2^x3^y\) is a one-to-one map from \(\N^2\) to \(\N\).
Show that there is a one-to-one map \(F:\N^2 \rightarrow \N\) such that for every \(x,y\), \(F(x,y) \leq 100\cdot \max\{x,y\}^2+100\).
For every \(k\), show that there is a one-to-one map \(F:\N^k \rightarrow \N\) such that for every \(x_0,\ldots,x_{k-1} \in \N\), \(F(x_0,\ldots,x_{k-1}) \leq 100 \cdot (x_0+x_1+\ldots+x_{k-1}+100k)^k\).
Prove that the NAND-CIRC program below computes the function \(\ensuremath{\mathit{MUX}}\) (or \(\ensuremath{\mathit{LOOKUP}}_1\)) where \(\ensuremath{\mathit{MUX}}(a,b,c)\) equals \(a\) if \(c=0\) and equals \(b\) if \(c=1\):
Give a NAND-CIRC program of at most 6 lines to compute the function \(\ensuremath{\mathit{MAJ}}:\{0,1\}^3 \rightarrow \{0,1\}\) where \(\ensuremath{\mathit{MAJ}}(a,b,c) = 1\) iff \(a+b+c \geq 2\).
In this exercise we will explore Theorem 4.6: transforming NAND-CIRC-IF programs that use code such as if .. then .. else .. to standard NAND-CIRC programs.
Give a “proof by code” of Theorem 4.6: a program in a programming language of your choice that transforms a NAND-CIRC-IF program \(P\) into a “sugar-free” NAND-CIRC program \(P'\) that computes the same function. See footnote for hint.4
Prove the following statement, which is the heart of Theorem 4.6: suppose that there exists an \(s\)-line NAND-CIRC program to compute \(f:\{0,1\}^n \rightarrow \{0,1\}\) and an \(s'\)-line NAND-CIRC program to compute \(g:\{0,1\}^n \rightarrow \{0,1\}\). Prove that there exist a NAND-CIRC program of at most \(s+s'+10\) lines to compute the function \(h:\{0,1\}^{n+1} \rightarrow \{0,1\}\) where \(h(x_0,\ldots,x_{n-1},x_n)\) equals \(f(x_0,\ldots,x_{n-1})\) if \(x_n=0\) and equals \(g(x_0,\ldots,x_{n-1})\) otherwise. (All programs in this item are standard “sugar-free” NAND-CIRC programs.)
A half adder is the function \(\ensuremath{\mathit{HA}}:\{0,1\}^2 :\rightarrow \{0,1\}^2\) that corresponds to adding two binary bits. That is, for every \(a,b \in \{0,1\}\), \(\ensuremath{\mathit{HA}}(a,b)= (e,f)\) where \(2e+f = a+b\). Prove that there is a NAND circuit of at most five NAND gates that computes \(\ensuremath{\mathit{HA}}\).
A full adder is the function \(\ensuremath{\mathit{FA}}:\{0,1\}^3 \rightarrow \{0,1\}^{2}\) that takes in two bits and a “carry” bit and outputs their sum. That is, for every \(a,b,c \in \{0,1\}\), \(\ensuremath{\mathit{FA}}(a,b,c) = (e,f)\) such that \(2e+f = a+b+c\). Prove that there is a NAND circuit of at most nine NAND gates that computes \(\ensuremath{\mathit{FA}}\).
Prove that if there is a NAND circuit of \(c\) gates that computes \(\ensuremath{\mathit{FA}}\), then there is a circuit of \(cn\) gates that computes \(\ensuremath{\mathit{ADD}}_n\) where (as in Theorem 4.7) \(\ensuremath{\mathit{ADD}}_n:\{0,1\}^{2n} \rightarrow \{0,1\}^{n+1}\) is the function that outputs the addition of two input \(n\)-bit numbers. See footnote for hint.5
Show that for every \(n\) there is a NAND-CIRC program to compute \(\ensuremath{\mathit{ADD}}_n\) with at most \(9n\) lines.
Write a program using your favorite programming language that on input of an integer \(n\), outputs a NAND-CIRC program that computes \(\ensuremath{\mathit{ADD}}_n\). Can you ensure that the program it outputs for \(\ensuremath{\mathit{ADD}}_n\) has fewer than \(10n\) lines?
Write a program using your favorite programming language that on input of an integer \(n\), outputs a NAND-CIRC program that computes \(\ensuremath{\mathit{MULT}}_n\). Can you ensure that the program it outputs for \(\ensuremath{\mathit{MULT}}_n\) has fewer than \(1000\cdot n^2\) lines?
Write a program using your favorite programming language that on input of an integer \(n\), outputs a NAND-CIRC program that computes \(\ensuremath{\mathit{MULT}}_n\) and has at most \(10000 n^{1.9}\) lines.6 What is the smallest number of lines you can use to multiply two 2048 bit numbers?
In the text Theorem 4.12 is only proven for the case \(m=1\). In this exercise you will extend the proof for every \(m\).
Prove that
If there is an \(s\)-line NAND-CIRC program to compute \(f:\{0,1\}^n \rightarrow \{0,1\}\) and an \(s'\)-line NAND-CIRC program to compute \(f':\{0,1\}^n \rightarrow \{0,1\}\) then there is an \(s+s'\)-line program to compute the function \(g:\{0,1\}^n \rightarrow \{0,1\}^2\) such that \(g(x)=(f(x),f'(x))\).
For every function \(f:\{0,1\}^n \rightarrow \{0,1\}^m\), there is a NAND-CIRC program of at most \(10m\cdot 2^n\) lines that computes \(f\). (You can use the \(m=1\) case of Theorem 4.12, as well as Item 1.)
Let \(P\) be the following NAND-CIRC program:
Temp[0] = NAND(X[0],X[0])
Temp[1] = NAND(X[1],X[1])
Temp[2] = NAND(Temp[0],Temp[1])
Temp[3] = NAND(X[2],X[2])
Temp[4] = NAND(X[3],X[3])
Temp[5] = NAND(Temp[3],Temp[4])
Temp[6] = NAND(Temp[2],Temp[2])
Temp[7] = NAND(Temp[5],Temp[5])
Y[0] = NAND(Temp[6],Temp[7])Write a program \(P'\) with at most three lines of code that uses both
NANDas well as the syntactic sugarORthat computes the same function as \(P\).Draw a circuit that computes the same function as \(P\) and uses only \(\ensuremath{\mathit{AND}}\) and \(\ensuremath{\mathit{NOT}}\) gates.
In the following exercises you are asked to compare the power of pairs of programming languages. By “comparing the power” of two programming languages \(X\) and \(Y\) we mean determining the relation between the set of functions that are computable using programs in \(X\) and \(Y\) respectively. That is, to answer such a question you need to do both of the following:
- Either prove that for every program \(P\) in \(X\) there is a program \(P'\) in \(Y\) that computes the same function as \(P\), or give an example for a function that is computable by an \(X\)-program but not computable by a \(Y\)-program.
and
- Either prove that for every program \(P\) in \(Y\) there is a program \(P'\) in \(X\) that computes the same function as \(P\), or give an example for a function that is computable by a \(Y\)-program but not computable by an \(X\)-program.
When you give an example as above of a function that is computable in one programming language but not the other, you need to prove that the function you showed is (1) computable in the first programming language and (2) not computable in the second programming language.
Let IF-CIRC be the programming language where we have the following operations foo = 0, foo = 1, foo = IF(cond,yes,no) (that is, we can use the constants \(0\) and \(1\), and the \(\ensuremath{\mathit{IF}}:\{0,1\}^3 \rightarrow \{0,1\}\) function such that \(\ensuremath{\mathit{IF}}(a,b,c)\) equals \(b\) if \(a=1\) and equals \(c\) if \(a=0\)). Compare the power of the NAND-CIRC programming language and the IF-CIRC programming language.
Let XOR-CIRC be the programming language where we have the following operations foo = XOR(bar,blah), foo = 1 and bar = 0 (that is, we can use the constants \(0\), \(1\) and the \(\ensuremath{\mathit{XOR}}\) function that maps \(a,b \in \{0,1\}^2\) to \(a+b \mod 2\)). Compare the power of the NAND-CIRC programming language and the XOR-CIRC programming language. See footnote for hint.7
Prove that there is some constant \(c\) such that for every \(n>1\), \(\ensuremath{\mathit{MAJ}}_n \in \ensuremath{\mathit{SIZE}}_n(cn)\) where \(\ensuremath{\mathit{MAJ}}_n:\{0,1\}^n \rightarrow \{0,1\}\) is the majority function on \(n\) input bits. That is \(\ensuremath{\mathit{MAJ}}_n(x)=1\) iff \(\sum_{i=0}^{n-1}x_i > n/2\). See footnote for hint.8
Prove that there is some constant \(c\) such that for every \(n>1\), and integers \(a_0,\ldots,a_{n-1},b \in \{-2^n,-2^n+1,\ldots,-1,0,+1,\ldots,2^n\}\), there is a NAND circuit with at most \(n^c\) gates that computes the threshold function \(f_{a_0,\ldots,a_{n-1},b}:\{0,1\}^n \rightarrow \{0,1\}\) that on input \(x\in \{0,1\}^n\) outputs \(1\) if and only if \(\sum_{i=0}^{n-1} a_i x_i > b\).
Bibliographical notes
See Jukna’s and Wegener’s books (Jukna, 2012) (Wegener, 1987) for much more extensive discussion on circuits. Shannon showed that every Boolean function can be computed by a circuit of exponential size (Shannon, 1938) . The improved bound of \(c \cdot 2^n/n\) (with the optimal value of \(c\) for many bases) is due to Lupanov (Lupanov, 1958) . An exposition of this for the case of NAND (where \(c=1\)) is given in Chapter 4 of his book (Lupanov, 1984) . (Thanks to Sasha Golovnev for tracking down this reference!)
The concept of “syntactic sugar” is also known as “macros” or “meta-programming” and is sometimes implemented via a preprocessor or macro language in a programming language or a text editor. One modern example is the Babel JavaScript syntax transformer, that converts JavaScript programs written using the latest features into a format that older Browsers can accept. It even has a plug-in architecture, that allows users to add their own syntactic sugar to the language.
- ↩
The value of \(c\) can be improved to \(9\), see Exercise 4.5.
- ↩
In case you are curious, this is the function on input \(i\in \{0,1\}^4\) (which we interpret as a number in \([16]\)), that outputs the \(i\)-th digit of \(\pi\) in the binary basis.
- ↩
The constant \(c\) in this theorem is at most \(10\) and in fact can be arbitrarily close to \(1\), see Section 4.8.
- ↩
You can start by transforming \(P\) into a NAND-CIRC-PROC program that uses procedure statements, and then use the code of Figure 4.3 to transform the latter into a “sugar-free” NAND-CIRC program.
- ↩
Use a “cascade” of adding the bits one after the other, starting with the least significant digit, just like in the elementary-school algorithm.
- ↩
Hint: Use Karatsuba’s algorithm.
- ↩
You can use the fact that \((a+b)+c \mod 2 = a+b+c \mod 2\). In particular it means that if you have the lines
d = XOR(a,b)ande = XOR(d,c)thenegets the sum modulo \(2\) of the variablea,bandc. - ↩
One approach to solve this is using recursion and the so-called Master Theorem.
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 12/06/2023 00:06:56
Copyright 2023, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.