See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
Loops and infinity
- Learn the model of Turing machines, which can compute functions of arbitrary input lengths.
- See a programming-language description of Turing machines, using NAND-TM programs, which add loops and arrays to NAND-CIRC.
- See some basic syntactic sugar and equivalence of variants of Turing machines and NAND-TM programs.
“The bounds of arithmetic were however outstepped the moment the idea of applying the [punched] cards had occurred; and the Analytical Engine does not occupy common ground with mere ‘calculating machines.’… In enabling mechanism to combine together general symbols, in successions of unlimited variety and extent, a uniting link is established between the operations of matter and the abstract mental processes of the most abstract branch of mathematical science.” , Ada Augusta, countess of Lovelace, 1843
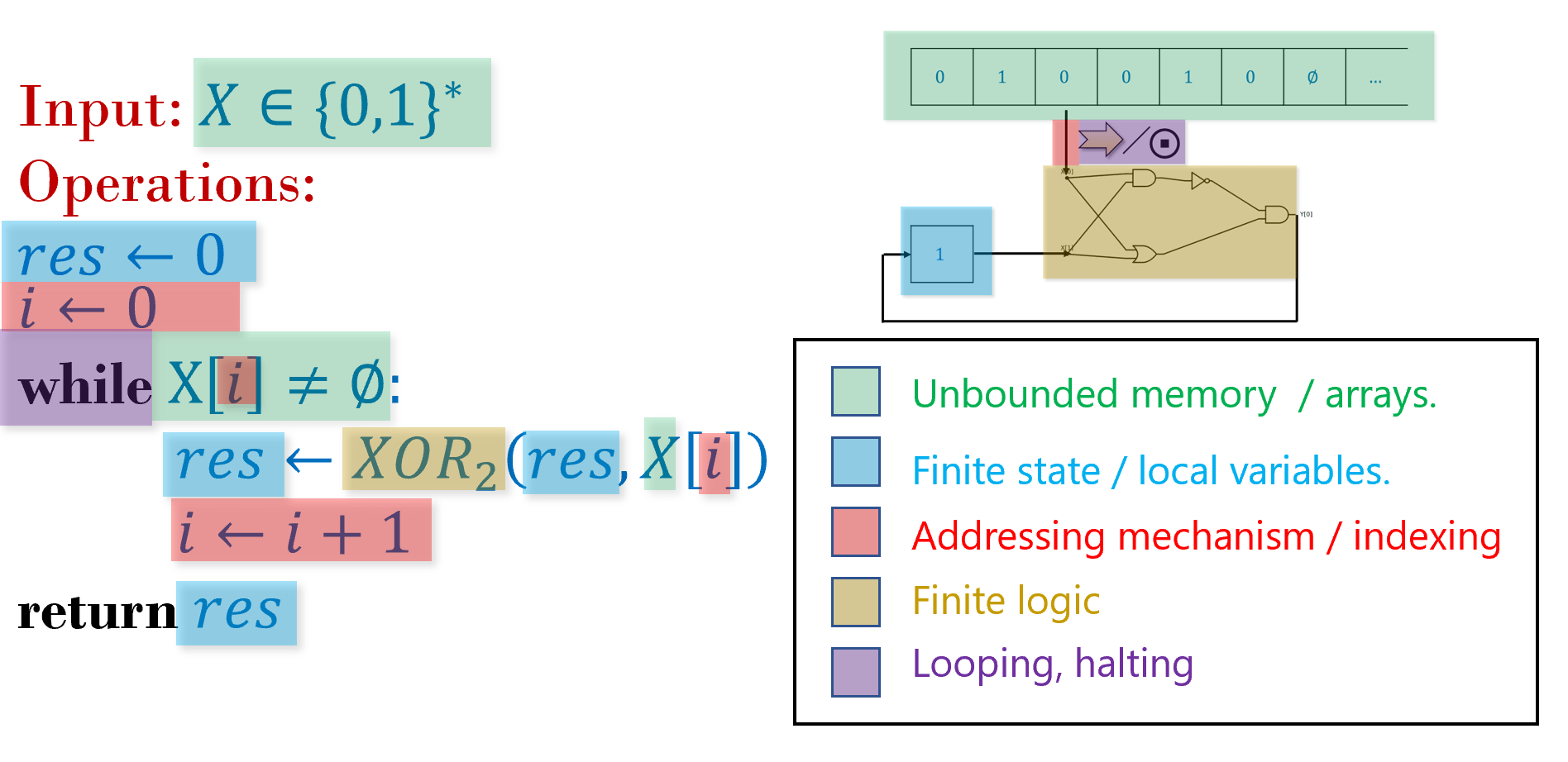
As the quote of Chapter 6 says, an algorithm is “a finite answer to an infinite number of questions”. To express an algorithm, we need to write down a finite set of instructions that will enable us to compute on arbitrarily long inputs. To describe and execute an algorithm we need the following components (see Figure 7.1):
The finite set of instructions to be performed.
Some “local variables” or finite state used in the execution.
A potentially unbounded working memory to store the input and any other values we may require later.
While the memory is unbounded, at every single step we can only read and write to a finite part of it, and we need a way to address which are the parts we want to read from and write to.
If we only have a finite set of instructions but our input can be arbitrarily long, we will need to repeat instructions (i.e., loop back). We need a mechanism to decide when we will loop and when we will halt.
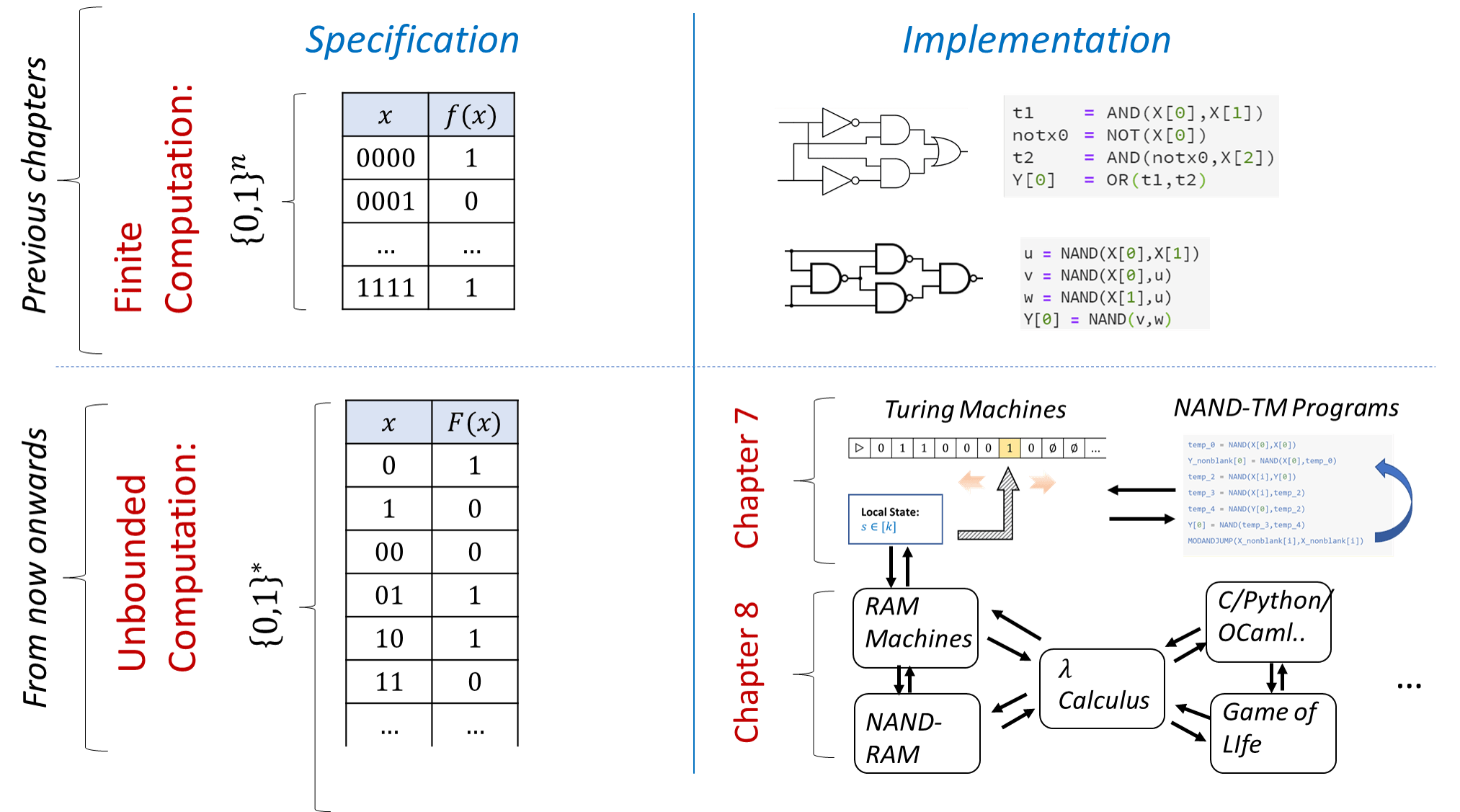
In this chapter, we give a general model of an algorithm, which (unlike Boolean circuits) is not restricted to a fixed input length, and (unlike finite automata) is not restricted to a finite amount of working memory. We will see two ways to model algorithms:
Turing machines, invented by Alan Turing in 1936, are hypothetical abstract devices that yield finite descriptions of algorithms that can handle arbitrarily long inputs.
The NAND-TM Programming language extends NAND-CIRC with the notion of loops and arrays to obtain finite programs that can compute a function with arbitrarily long inputs.
It turns out that these two models are equivalent. In fact, they are equivalent to many other computational models, including programming languages such as C, Lisp, Python, JavaScript, etc. This notion, known as Turing equivalence or Turing completeness, will be discussed in Chapter 8. See Figure 7.2 for an overview of the models presented in this chapter and Chapter 8.
Turing Machines
“Computing is normally done by writing certain symbols on paper. We may suppose that this paper is divided into squares like a child’s arithmetic book.. The behavior of the [human] computer at any moment is determined by the symbols which he is observing, and of his’ state of mind’ at that moment… We may suppose that in a simple operation not more than one symbol is altered.” ,
“We compare a man in the process of computing … to a machine which is only capable of a finite number of configurations… The machine is supplied with a ‘tape’ (the analogue of paper) … divided into sections (called ‘squares’) each capable of bearing a ‘symbol’” , Alan Turing, 1936
“What is the difference between a Turing machine and the modern computer? It’s the same as that between Hillary’s ascent of Everest and the establishment of a Hilton hotel on its peak.” , Alan Perlis, 1982.

The “granddaddy” of all models of computation is the Turing machine. Turing machines were defined in 1936 by Alan Turing in an attempt to formally capture all the functions that can be computed by human “computers” (see Figure 7.4) that follow a well-defined set of rules, such as the standard algorithms for addition or multiplication.

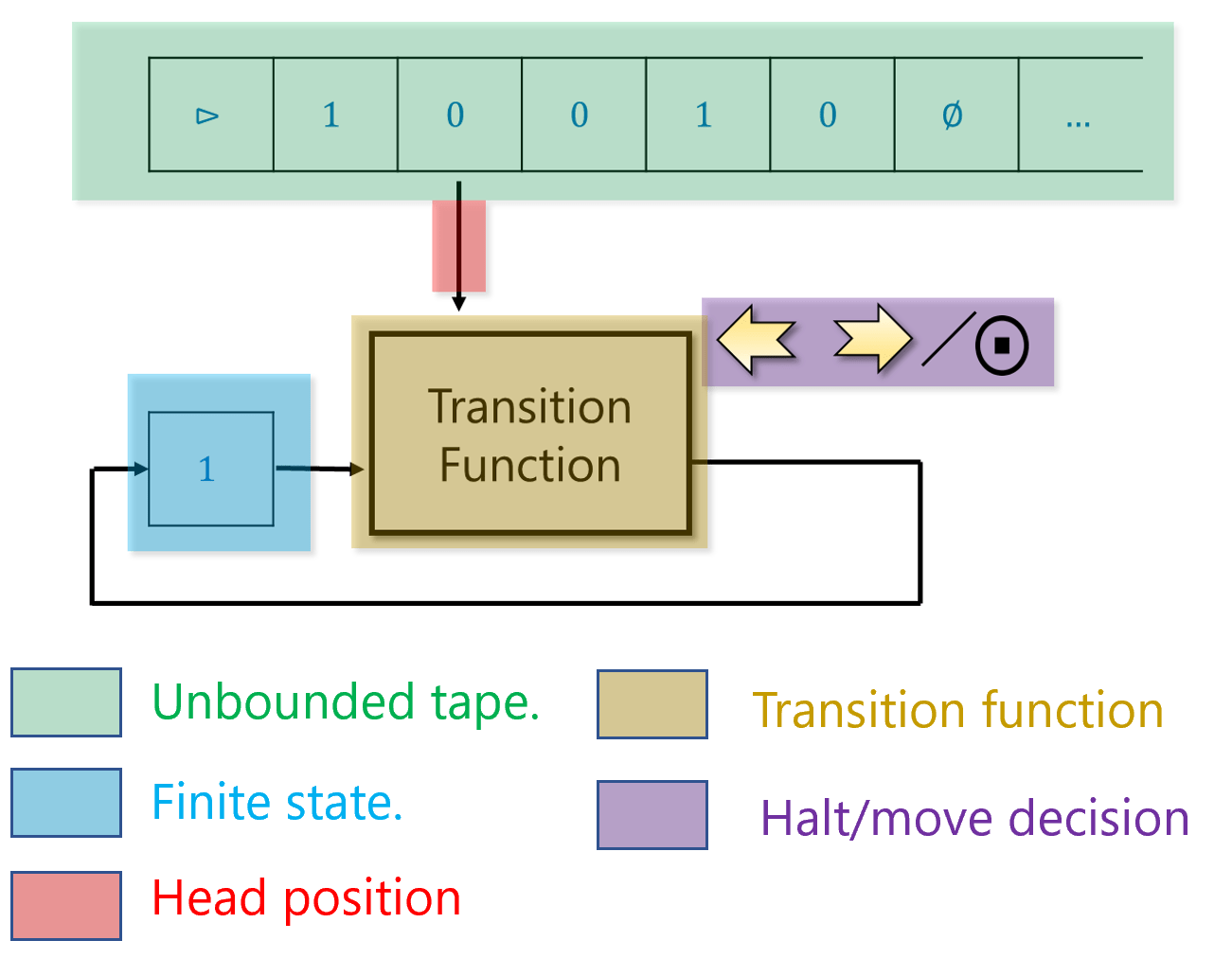
Turing thought of such a person as having access to as much “scratch paper” as they need. For simplicity, we can think of this scratch paper as a one dimensional piece of graph paper (or tape, as it is commonly referred to). The paper is divided into “cells”, where each “cell” can hold a single symbol (e.g., one digit or letter, and more generally, some element of a finite alphabet). At any point in time, the person can read from and write to a single cell of the paper. Based on the contents of this cell, the person can update their finite mental state, and/or move to the cell immediately to the left or right of the current one.

Turing modeled such a computation by a “machine” that maintains one of \(k\) states. At each point in time the machine reads from its “work tape” a single symbol from a finite alphabet \(\Sigma\) and uses that to update its state, write to tape, and possibly move to an adjacent cell (see Figure 7.7). To compute a function \(F\) using this machine, we initialize the tape with the input \(x\in \{0,1\}^*\) and our goal is to ensure that the tape will contain the value \(F(x)\) at the end of the computation. Specifically, a computation of a Turing machine \(M\) with \(k\) states and alphabet \(\Sigma\) on input \(x\in \{0,1\}^*\) proceeds as follows:
Initially the machine is at state \(0\) (known as the “starting state”) and the tape is initialized to \(\triangleright,x_0,\ldots,x_{n-1},\varnothing,\varnothing,\ldots\). We use the symbol \(\triangleright\) to denote the beginning of the tape, and the symbol \(\varnothing\) to denote an empty cell. We will always assume that the alphabet \(\Sigma\) is a (potentially strict) superset of \(\{ \triangleright, \varnothing , 0 , 1 \}\).
The location \(i\) to which the machine points to is set to \(0\).
At each step, the machine reads the symbol \(\sigma = T[i]\) that is in the \(i^{th}\) location of the tape. Based on this symbol and its state \(s\), the machine decides on:
- What symbol \(\sigma'\) to write on the tape
- Whether to move Left (i.e., \(i \leftarrow i-1\)), Right (i.e., \(i \leftarrow i+1\)), Stay in place, or Halt the computation.
- What is going to be the new state \(s \in [k]\)
- What symbol \(\sigma'\) to write on the tape
The set of rules the Turing machine follows is known as its transition function.
When the machine halts, its output is the binary string obtained by reading the tape from the beginning until the first location in which it contains a \(\varnothing\) symbol, and then outputting all \(0\) and \(1\) symbols in sequence, dropping the initial \(\triangleright\) symbol if it exists, as well as the final \(\varnothing\) symbol.
Extended example: A Turing machine for palindromes
Let \(\ensuremath{\mathit{PAL}}\) (for palindromes) be the function that on input \(x\in \{0,1\}^*\), outputs \(1\) if and only if \(x\) is an (even length) palindrome, in the sense that \(x = w_0 \cdots w_{n-1}w_{n-1}w_{n-2}\cdots w_0\) for some \(n\in \N\) and \(w\in \{0,1\}^n\).
We now show a Turing machine \(M\) that computes \(\ensuremath{\mathit{PAL}}\). To specify \(M\) we need to specify (i) \(M\)’s tape alphabet \(\Sigma\) which should contain at least the symbols \(0\),\(1\), \(\triangleright\) and \(\varnothing\), and (ii) \(M\)’s transition function which determines what action \(M\) takes when it reads a given symbol while it is in a particular state.
In our case, \(M\) will use the alphabet \(\{ 0,1,\triangleright, \varnothing, \times \}\) and will have \(k=11\) states. Though the states are simply numbers between \(0\) and \(k-1\), we will give them the following labels for convenience:
State |
Label |
|---|---|
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
We describe the operation of our Turing machine \(M\) in words:
\(M\) starts in state
STARTand goes right, looking for the first symbol that is \(0\) or \(1\). If it finds \(\varnothing\) before it hits such a symbol then it moves to theOUTPUT_1state described below.Once \(M\) finds such a symbol \(b \in \{0,1\}\), \(M\) deletes \(b\) from the tape by writing the \(\times\) symbol, it enters either the
RIGHT_\(b\) mode and starts moving rightwards until it hits the first \(\varnothing\) or \(\times\) symbol.Once \(M\) finds this symbol, it goes into the state
LOOK_FOR_0orLOOK_FOR_1depending on whether it was in the stateRIGHT_0orRIGHT_1and makes one left move.In the state
LOOK_FOR_\(b\), \(M\) checks whether the value on the tape is \(b\). If it is, then \(M\) deletes it by changing its value to \(\times\), and moves to the stateRETURN. Otherwise, it changes to theOUTPUT_0state.The
RETURNstate means that \(M\) goes back to the beginning. Specifically, \(M\) moves leftward until it hits the first symbol that is not \(0\) or \(1\), in which case it changes its state toSTART.The
OUTPUT_\(b\) states mean that \(M\) will eventually output the value \(b\). In both theOUTPUT_0andOUTPUT_1states, \(M\) goes left until it hits \(\triangleright\). Once it does so, it makes a right step, and changes to the1_AND_BLANKor0_AND_BLANKstates respectively. In the latter states, \(M\) writes the corresponding value, moves right and changes to theBLANK_AND_STOPstate, in which it writes \(\varnothing\) to the tape and halts.
The above description can be turned into a table describing for each one of the \(11\cdot 5\) combination of state and symbol, what the Turing machine will do when it is in that state and it reads that symbol. This table is known as the transition function of the Turing machine.
Turing machines: a formal definition
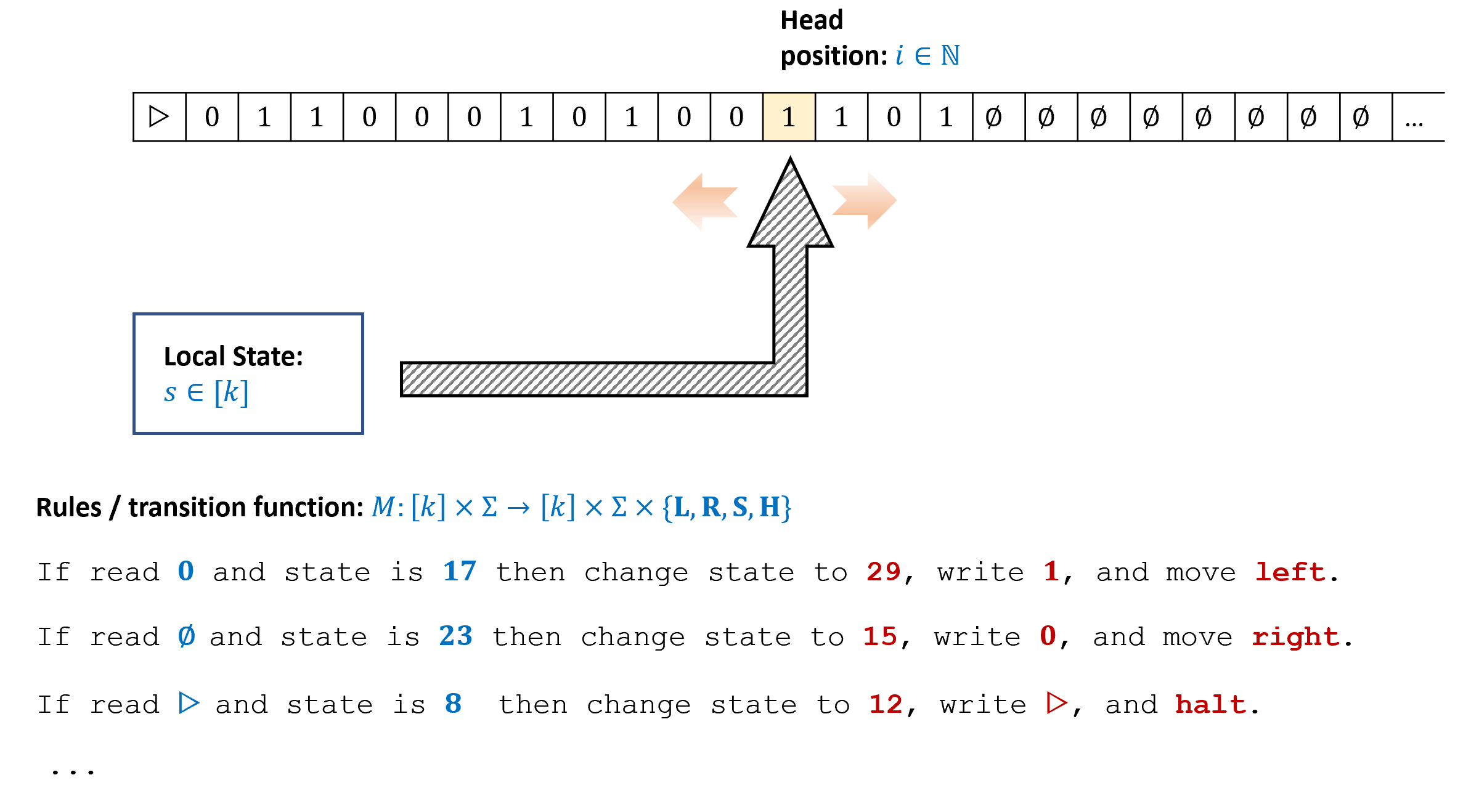
The formal definition of Turing machines is as follows:
A (one tape) Turing machine \(M\) with \(k\) states and alphabet \(\Sigma \supseteq \{0,1, \triangleright, \varnothing \}\) is represented by a transition function \(\delta_M:[k]\times \Sigma \rightarrow [k] \times \Sigma \times \{\mathsf{L},\mathsf{R}, \mathsf{S}, \mathsf{H} \}\).
For every \(x\in \{0,1\}^*\), the output of \(M\) on input \(x\), denoted by \(M(x)\), is the result of the following process:
We initialize \(T\) to be the sequence \(\triangleright,x_0,x_1,\ldots,x_{n-1},\varnothing,\varnothing,\ldots\), where \(n=|x|\). (That is, \(T[0]=\triangleright\), \(T[i+1]=x_{i}\) for \(i\in [n]\), and \(T[i]=\varnothing\) for \(i>n\).)
We also initialize \(i=0\) and \(s=0\).
We then repeat the following process:
- Let \((s',\sigma',D) = \delta_M(s,T[i])\).
- Set \(s \leftarrow s'\), \(T[i] \leftarrow \sigma'\).
- If \(D=\mathsf{R}\) then set \(i \rightarrow i+1\), if \(D=\mathsf{L}\) then set \(i \rightarrow \max\{i-1,0\}\). (If \(D = \mathsf{S}\) then we keep \(i\) the same.)
- If \(D=\mathsf{H}\), then halt.
If the process above halts, then \(M\)’s output, denoted by \(M(x)\), is the string \(y\in \{0,1\}^*\) obtained by concatenating all the symbols in \(\{0,1\}\) in positions \(T[0],\ldots, T[i]\) where \(i+1\) is the first location in the tape containing \(\varnothing\).
If The Turing machine does not halt then we denote \(M(x)=\bot\).
You should make sure you see why this formal definition corresponds to our informal description of a Turing machine. To get more intuition on Turing machines, you can explore some of the online available simulators such as Martin Ugarte’s, Anthony Morphett’s, or Paul Rendell’s.
One should not confuse the transition function \(\delta_M\) of a Turing machine \(M\) with the function that the machine computes. The transition function \(\delta_M\) is a finite function, with \(k|\Sigma|\) inputs and \(4k|\Sigma|\) outputs. (Can you see why?) The machine can compute an infinite function \(F\) that takes as input a string \(x\in \{0,1\}^*\) of arbitrary length and might also produce an arbitrary length string as output.
In our formal definition, we identified the machine \(M\) with its transition function \(\delta_M\) since the transition function tells us everything we need to know about the Turing machine. However, this choice of representation is somewhat arbitrary, and is based on our convention that the state space is always the numbers \(\{0,\ldots,k-1\}\) with \(0\) as the starting state. Other texts use different conventions, and so their mathematical definition of a Turing machine might look superficially different. However, these definitions describe the same computational process and have the same computational powers. Hence they are equivalent despite their superficial differences. See Section 7.7 for a comparison between Definition 7.1 and the way Turing Machines are defined in texts such as Sipser (Sipser, 1997) .
Computable functions
We now turn to make one of the most important definitions in this book: computable functions.
Let \(F:\{0,1\}^* \rightarrow \{0,1\}^*\) be a (total) function and let \(M\) be a Turing machine. We say that \(M\) computes \(F\) if for every \(x\in \{0,1\}^*\), \(M(x)=F(x)\).
We say that a function \(F\) is computable if there exists a Turing machine \(M\) that computes it.
Defining a function “computable” if and only if it can be computed by a Turing machine might seem “reckless” but, as we’ll see in Chapter 8, being computable in the sense of Definition 7.2 is equivalent to being computable in virtually any reasonable model of computation. This statement is known as the Church-Turing Thesis. (Unlike the extended Church-Turing Thesis which we discussed in Section 5.6, the Church-Turing thesis itself is widely believed and there are no candidate devices that attack it.)
We can precisely define what it means for a function to be computable by any possible algorithm.
This is a good point to remind the reader that functions are not the same as programs:
A Turing machine (or program) \(M\) can compute some function \(F\), but it is not the same as \(F\). In particular, there can be more than one program to compute the same function. Being computable is a property of functions, not of machines.
We will often pay special attention to functions \(F:\{0,1\}^* \rightarrow \{0,1\}\) that have a single bit of output. Hence we give a special name for the set of computable functions of this form.
We define \(\mathbf{R}\) be the set of all computable functions \(F:\{0,1\}^* \rightarrow \{0,1\}\).
As discussed in Section 6.1.2, many texts use the terminology of “languages” rather than functions to refer to computational tasks. A Turing machine \(M\) decides a language \(L\) if for every input \(x\in \{0,1\}^*\), \(M(x)\) outputs \(1\) if and only if \(x\in L\). This is equivalent to computing the Boolean function \(F:\{0,1\}^* \rightarrow \{0,1\}\) defined as \(F(x)=1\) iff \(x\in L\). A language \(L\) is decidable if there is a Turing machine \(M\) that decides it. For historical reasons, some texts also call such languages recursive , which is the reason that the letter \(\mathbf{R}\) is often used to denote the set of computable Boolean functions / decidable languages defined in Definition 7.3.
In this book we stick to the terminology of functions rather than languages, but all definitions and results can be easily translated back and forth by using the equivalence between the function \(F:\{0,1\}^* \rightarrow \{0,1\}\) and the language \(L = \{ x\in \{0,1\}^* \;|\; F(x) = 1 \}\).
Infinite loops and partial functions
One crucial difference between circuits/straight-line programs and Turing machines is the following. Looking at a NAND-CIRC program \(P\), we can always tell how many inputs and how many outputs \(P\) has by simply looking at the X and Y variables. Furthermore, we are guaranteed that if we invoke \(P\) on any input, then some output will be produced.
In contrast, given a Turing machine \(M\), we cannot determine a priori the length of \(M\)’s output. In fact, we don’t even know if an output would be produced at all! For example, it is straightforward to come up with a Turing machine whose transition function never outputs \(\mathsf{H}\) and hence never halts.
If a machine \(M\) fails to stop and produce an output on some input \(x\), then it cannot compute any total function \(F\), since clearly on input \(x\), \(M\) will fail to output \(F(x)\). However, \(M\) can still compute a partial function.1
For example, consider the partial function \(\ensuremath{\mathit{DIV}}\) that on input a pair \((a,b)\) of natural numbers, outputs \(\ceil{a/b}\) if \(b > 0\), and is undefined otherwise. We can define a Turing machine \(M\) that computes \(\ensuremath{\mathit{DIV}}\) on input \(a,b\) by outputting the first \(c=0,1,2,\ldots\) such that \(cb \geq a\). If \(a>0\) and \(b=0\) then the machine \(M\) will never halt, but this is OK, since \(\ensuremath{\mathit{DIV}}\) is undefined on such inputs. If \(a=0\) and \(b=0\), the machine \(M\) will output \(0\), which is also OK, since we don’t care about what the program outputs on inputs on which \(\ensuremath{\mathit{DIV}}\) is undefined. Formally, we define computability of partial functions as follows:
Let \(F\) be either a total or partial function mapping \(\{0,1\}^*\) to \(\{0,1\}^*\) and let \(M\) be a Turing machine. We say that \(M\) computes \(F\) if for every \(x\in \{0,1\}^*\) on which \(F\) is defined, \(M(x)=F(x)\). We say that a (partial or total) function \(F\) is computable if there is a Turing machine that computes it.
Note that if \(F\) is a total function, then it is defined on every \(x\in \{0,1\}^*\) and hence in this case, Definition 7.5 is identical to Definition 7.2.
We often use \(\bot\) as our special “failure symbol”. If a Turing machine \(M\) fails to halt on some input \(x\in \{0,1\}^*\) then we denote this by \(M(x) = \bot\). This does not mean that \(M\) outputs some encoding of the symbol \(\bot\) but rather that \(M\) enters into an infinite loop when given \(x\) as input.
If a partial function \(F\) is undefined on \(x\) then we can also write \(F(x) = \bot\). Therefore one might think that Definition 7.5 can be simplified to requiring that \(M(x) = F(x)\) for every \(x\in \{0,1\}^*\), which would imply that for every \(x\), \(M\) halts on \(x\) if and only if \(F\) is defined on \(x\). However, this is not the case: for a Turing machine \(M\) to compute a partial function \(F\) it is not necessary for \(M\) to enter an infinite loop on inputs \(x\) on which \(F\) is not defined. All that is needed is for \(M\) to output \(F(x)\) on values of \(x\) on which \(F\) is defined: on other inputs it is OK for \(M\) to output an arbitrary value such as \(0\), \(1\), or anything else, or not to halt at all. To borrow a term from the C programming language, on inputs \(x\) on which \(F\) is not defined, what \(M\) does is “undefined behavior”.
Turing machines as programming languages
The name “Turing machine”, with its “tape” and “head” evokes a physical object, while in contrast we think of a program as a piece of text. But we can think of a Turing machine as a program as well. For example, consider the Turing machine \(M\) of Section 7.1.1 that computes the function \(\ensuremath{\mathit{PAL}}\) such that \(\ensuremath{\mathit{PAL}}(x)=1\) iff \(x\) is a palindrome. We can also describe this machine as a program using the Python-like pseudocode of the form below
# Gets an array Tape initialized to
# [">", x_0 , x_1 , .... , x_(n-1), "∅", "∅", ...]
# At the end of the execution, Tape[1] is equal to 1
# if x is a palindrome and is equal to 0 otherwise
def PAL(Tape):
head = 0
state = 0 # START
while (state != 12):
if (state == 0 && Tape[head]=='0'):
state = 3 # LOOK_FOR_0
Tape[head] = 'x'
head += 1 # move right
if (state==0 && Tape[head]=='1')
state = 4 # LOOK_FOR_1
Tape[head] = 'x'
head += 1 # move right
... # more if statements hereThe precise details of this program are not important. What matters is that we can describe Turing machines as programs. Moreover, note that when translating a Turing machine into a program, the tape becomes a list or array that can hold values from the finite set \(\Sigma\).2 The head position can be thought of as an integer-valued variable that holds integers of unbounded size. The state is a local register that can hold one of a fixed number of values in \([k]\).
More generally we can think of every Turing machine \(M\) as equivalent to a program similar to the following:
# Gets an array Tape initialized to
# [">", x_0 , x_1 , .... , x_(n-1), "∅", "∅", ...]
def M(Tape):
state = 0
i = 0 # holds head location
while (True):
# Move head, modify state, write to tape
# based on current state and cell at head
# below are just examples for how program looks for a particular transition function
if Tape[i]=="0" and state==7: # δ_M(7,"0")=(19,"1","R")
Tape[i]="1"
i += 1
state = 19
elif Tape[i]==">" and state == 13: # δ_M(13,">")=(15,"0","S")
Tape[i]="0"
state = 15
elif ...
...
elif Tape[i]==">" and state == 29: # δ_M(29,">")=(.,.,"H")
break # HaltIf we wanted to use only Boolean (i.e., \(0\)/\(1\)-valued) variables, then we can encode the state variables using \(\ceil{\log k}\) bits. Similarly, we can represent each element of the alphabet \(\Sigma\) using \(\ell=\ceil{\log |\Sigma|}\) bits and hence we can replace the \(\Sigma\)-valued array Tape[] with \(\ell\) Boolean-valued arrays Tape0[],\(\ldots\), Tape\((\ell - 1)\)[].
The NAND-TM Programming language
We now introduce the NAND-TM programming language, which captures the power of a Turing machine with a programming-language formalism. Like the difference between Boolean circuits and Turing machines, the main difference between NAND-TM and NAND-CIRC is that NAND-TM models a single uniform algorithm that can compute a function that takes inputs of arbitrary lengths. To do so, we extend the NAND-CIRC programming language with two constructs:
Loops: NAND-CIRC is a straight-line programming language- a NAND-CIRC program of \(s\) lines takes exactly \(s\) steps of computation and hence in particular, cannot even touch more than \(3s\) variables. Loops allow us to use a fixed-length program to encode the instructions for a computation that can take an arbitrary amount of time.
Arrays: A NAND-CIRC program of \(s\) lines touches at most \(3s\) variables. While we can use variables with names such as
Foo_17orBar[22]in NAND-CIRC, they are not true arrays, since the number in the identifier is a constant that is “hardwired” into the program. NAND-TM contains actual arrays that can have a length that is not a priori bounded.
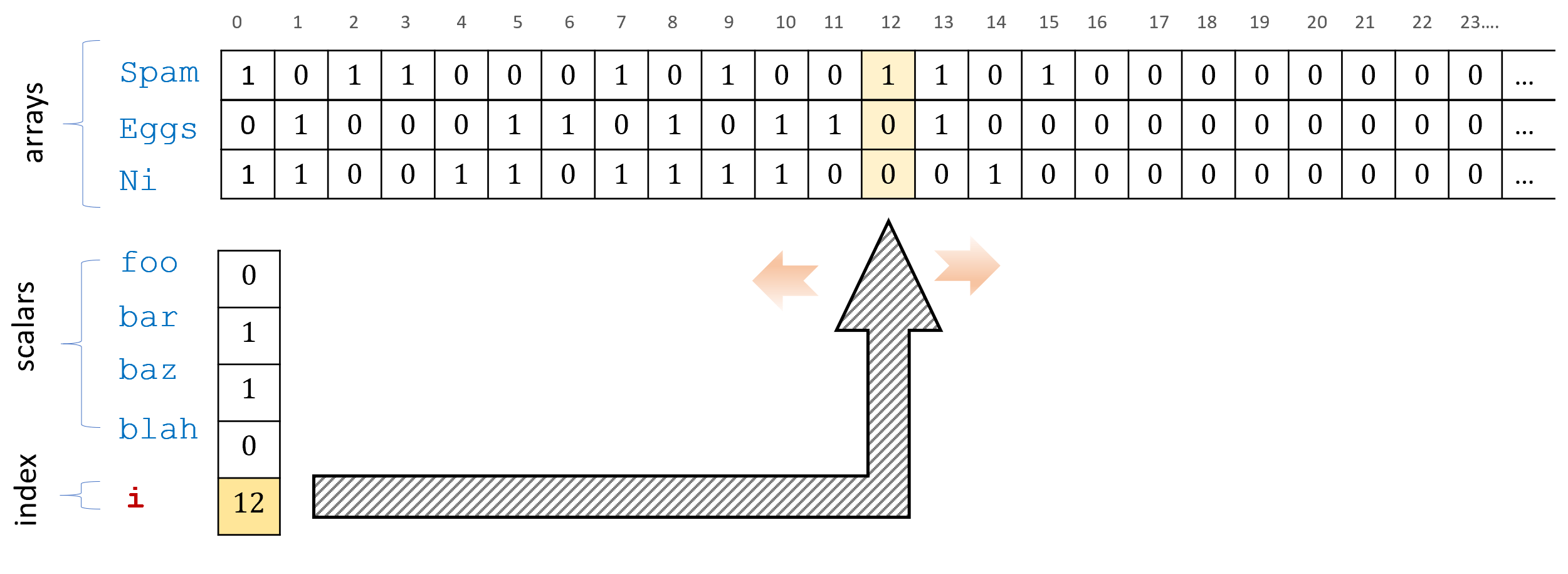
i that can be used to index the array variables. We refer to the i-th value of the array variable Spam using Spam[i]. At each iteration of the program the index variable can be incremented or decremented by one step using the MODANDJUMP operation.Thus a good way to remember NAND-TM is using the following informal equation:
As we will see, adding loops and arrays to NAND-CIRC is enough to capture the full power of all programming languages! Hence we could replace “NAND-TM” with any of Python, C, Javascript, OCaml, etc. in the left-hand side of Equation 7.1. But we’re getting ahead of ourselves: this issue will be discussed in Chapter 8.
Concretely, the NAND-TM programming language adds the following features on top of NAND-CIRC (see Figure 7.8):
We add a special integer valued variable
i. All other variables in NAND-TM are Boolean valued (as in NAND-CIRC).Apart from
iNAND-TM has two kinds of variables: scalars and arrays. Scalar variables hold one bit (just as in NAND-CIRC). Array variables hold an unbounded number of bits. At any point in the computation we can access the array variables at the location indexed byiusingFoo[i]. We cannot access the arrays at locations other than the one pointed to byi.We use the convention that arrays always start with a capital letter, and scalar variables (which are never indexed with
i) start with lowercase letters. HenceFoois an array andbaris a scalar variable.The input and output
XandYare now considered arrays with values of zeroes and ones. (There are also two other special arraysX_nonblankandY_nonblank, see below.)We add a special
MODANDJUMPinstruction that takes two Boolean variables \(a,b\) as input and does the following:- If \(a=1\) and \(b=1\) then
MODANDJUMP(\(a,b\))incrementsiby one and jumps to the first line of the program. - If \(a=0\) and \(b=1\) then
MODANDJUMP(\(a,b\))decrementsiby one and jumps to the first line of the program. (Ifiis already equal to \(0\) then it stays at \(0\).) - If \(a=1\) and \(b=0\) then
MODANDJUMP(\(a,b\))jumps to the first line of the program without modifyingi. - If \(a=b=0\) then
MODANDJUMP(\(a,b\))halts execution of the program.
- If \(a=1\) and \(b=1\) then
The
MODANDJUMPinstruction always appears in the last line of a NAND-TM program and nowhere else.
Default values. We need one more convention to handle “default values”. Turing machines have the special symbol \(\varnothing\) to indicate that tape location is “blank” or “uninitialized”. In NAND-TM there is no such symbol, and all variables are Boolean, containing either \(0\) or \(1\). All variables and locations of arrays default to \(0\) if they have not been initialized to another value. To keep track of whether a \(0\) in an array corresponds to a true zero or to an uninitialized cell, a programmer can always add to an array Foo a “companion array” Foo_nonblank and set Foo_nonblank[i] to \(1\) whenever the i th location is initialized. In particular, we will use this convention for the input and output arrays X and Y. A NAND-TM program has four special arrays X, X_nonblank, Y, and Y_nonblank. When a NAND-TM program is executed on input \(x\in \{0,1\}^*\) of length \(n\), the first \(n\) cells of the array X are initialized to \(x_0,\ldots,x_{n-1}\) and the first \(n\) cells of the array X_nonblank are initialized to \(1\). (All uninitialized cells default to \(0\).) The output of a NAND-TM program is the string Y[\(0\)], \(\ldots\), Y[\(m-1\)] where \(m\) is the smallest integer such that Y_nonblank[\(m\)]\(=0\). A NAND-TM program gets called with X and X_nonblank initialized to contain the input, and writes to Y and Y_nonblank to produce the output.
Formally, NAND-TM programs are defined as follows:
A NAND-TM program consists of a sequence of lines of the form foo = NAND(bar,blah) ending with a line of the form MODANDJUMP(foo,bar), where foo,bar,blah are either scalar variables (sequences of letters, digits, and underscores) or array variables of the form Foo[i] (starting with capital letters and indexed by i). The program has the array variables X, X_nonblank, Y, Y_nonblank and the index variable i built in, and can use additional array and scalar variables.
If \(P\) is a NAND-TM program and \(x\in \{0,1\}^*\) is an input then an execution of \(P\) on \(x\) is the following process:
The arrays
XandX_nonblankare initialized byX[\(i\)]\(=x_i\) andX_nonblank[\(i\)]\(=1\) for all \(i\in [|x|]\). All other variables and cells are initialized to \(0\). The index variableiis also initialized to \(0\).The program is executed line by line. When the last line
MODANDJUMP(foo,bar)is executed we do as follows:If
foo\(=1\) andbar\(=0\), jump to the first line without modifying the value ofi.If
foo\(=1\) andbar\(=1\), incrementiby one and jump to the first line.If
foo\(=0\) andbar\(=1\), decrementiby one (unless it is already zero) and jump to the first line.If
foo\(=0\) andbar\(=0\), halt and outputY[\(0\)], \(\ldots\),Y[\(m-1\)]where \(m\) is the smallest integer such thatY_nonblank[\(m\)]\(=0\).
Sneak peak: NAND-TM vs Turing machines
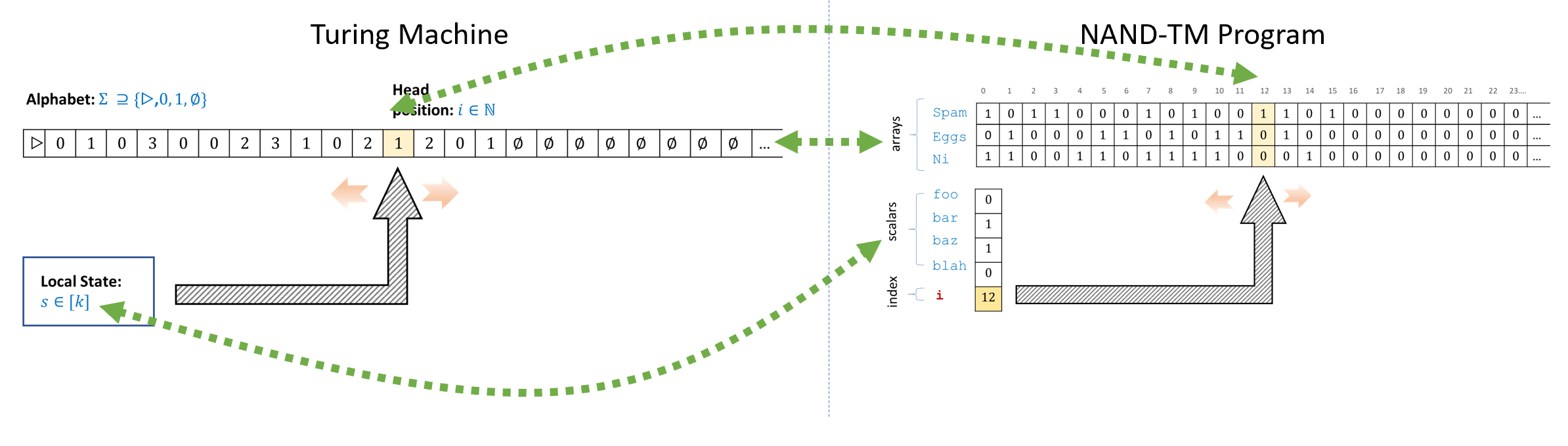
As the name implies, NAND-TM programs are a direct implementation of Turing machines in programming language form. We will show the equivalence below, but you can already see how the components of Turing machines and NAND-TM programs correspond to one another:
Turing Machine |
NAND-TM program |
|---|---|
State: single register that takes values in \([k]\) |
Scalar variables: Several variables such as |
Tape: One tape containing values in a finite set \(\Sigma\). Potentially infinite but \(T[t]\) defaults to \(\varnothing\) for all locations \(t\) that have not been accessed. |
Arrays: Several arrays such as |
Head location: A number \(i\in \mathbb{N}\) that encodes the position of the head. |
Index variable: The variable |
Accessing memory: At every step the Turing machine has access to its local state, but can only access the tape at the position of the current head location. |
Accessing memory: At every step a NAND-TM program has access to all the scalar variables, but can only access the arrays at the location |
Control of location: In each step the machine can move the head location by at most one position. |
Control of index variable: In each iteration of its main loop the program can modify the index |
Examples
We now present some examples of NAND-TM programs.
The following is a NAND-TM program to compute the increment function. That is, \(\ensuremath{\mathit{INC}}:\{0,1\}^* \rightarrow \{0,1\}^*\) such that for every \(x\in \{0,1\}^n\), \(\ensuremath{\mathit{INC}}(x)\) is the \(n+1\) bit long string \(y\) such that if \(X = \sum_{i=0}^{n-1}x_i \cdot 2^i\) is the number represented by \(x\), then \(y\) is the (least-significant digit first) binary representation of the number \(X+1\).
We start by describing the program using “syntactic sugar” for NAND-CIRC for the IF, XOR and AND functions (as well as the constant one function, and the function COPY that just maps a bit to itself).
carry = IF(started,carry,one(started))
started = one(started)
Y[i] = XOR(X[i],carry)
carry = AND(X[i],carry)
Y_nonblank[i] = one(started)
MODANDJUMP(X_nonblank[i],X_nonblank[i])Since we used syntactic sugar, the above is not, strictly speaking, a valid NAND-TM program. However, by “opening up” all the syntactic sugar, we get the following “sugar free” valid program to compute the same function.
temp_0 = NAND(started,started)
temp_1 = NAND(started,temp_0)
temp_2 = NAND(started,started)
temp_3 = NAND(temp_1,temp_2)
temp_4 = NAND(carry,started)
carry = NAND(temp_3,temp_4)
temp_6 = NAND(started,started)
started = NAND(started,temp_6)
temp_8 = NAND(X[i],carry)
temp_9 = NAND(X[i],temp_8)
temp_10 = NAND(carry,temp_8)
Y[i] = NAND(temp_9,temp_10)
temp_12 = NAND(X[i],carry)
carry = NAND(temp_12,temp_12)
temp_14 = NAND(started,started)
Y_nonblank[i] = NAND(started,temp_14)
MODANDJUMP(X_nonblank[i],X_nonblank[i])The following is a NAND-TM program to compute the XOR function on inputs of arbitrary length. That is \(\ensuremath{\mathit{XOR}}:\{0,1\}^* \rightarrow \{0,1\}\) such that \(\ensuremath{\mathit{XOR}}(x) = \sum_{i=0}^{|x|-1} x_i \mod 2\) for every \(x\in \{0,1\}^*\). Once again, we use a certain “syntactic sugar”. Specifically, we access the arrays X and Y at their zero-th entry, while NAND-TM only allows access to arrays in the coordinate of the variable i.
temp_0 = NAND(X[0],X[0])
Y_nonblank[0] = NAND(X[0],temp_0)
temp_2 = NAND(X[i],Y[0])
temp_3 = NAND(X[i],temp_2)
temp_4 = NAND(Y[0],temp_2)
Y[0] = NAND(temp_3,temp_4)
MODANDJUMP(X_nonblank[i],X_nonblank[i])To transform the program above to a valid NAND-TM program, we can transform references such as X[0] and Y[0] to scalar variables x_0 and y_0 (similarly we can transform any reference of the form Foo[17] or Bar[15] to scalars such as foo_17 and bar_15). We then need to add code to load the value of X[0] to x_0 and similarly to write to Y[0] the value of y_0, but this is not hard to do. Using the fact that variables are initialized to zero by default, we can create a variable init which will be set to \(1\) at the end of the first iteration and not changed since then. We can then add an array Atzero and code that will modify Atzero[i] to \(1\) if init is \(0\) and otherwise leave it as it is. This will ensure that Atzero[i] is equal to \(1\) if and only if i is set to zero, and allow the program to know when we are at the zeroth location. Thus we can add code to read and write to the corresponding scalars x_0, y_0 when we are at the zeroth location, and also code to move i to zero and then halt at the end. Working this out fully is somewhat tedious, but can be a good exercise.
Working out the above two examples can go a long way towards understanding the NAND-TM language. See our GitHub repository for a full specification of the NAND-TM language.
Equivalence of Turing machines and NAND-TM programs
Given the above discussion, it might not be surprising that Turing machines turn out to be equivalent to NAND-TM programs. Indeed, we designed the NAND-TM language to have this property. Nevertheless, this is a significant result, and the first of many other such equivalence results we will see in this book.
For every \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), \(F\) is computable by a NAND-TM program \(P\) if and only if there is a Turing machine \(M\) that computes \(F\).
To prove such an equivalence theorem, we need to show two directions. We need to be able to (1) transform a Turing machine \(M\) to a NAND-TM program \(P\) that computes the same function as \(M\) and (2) transform a NAND-TM program \(P\) into a Turing machine \(M\) that computes the same function as \(P\).
The idea of the proof is illustrated in Figure 7.9. To show (1), given a Turing machine \(M\), we will create a NAND-TM program \(P\) that will have an array Tape for the tape of \(M\) and scalar (i.e., non-array) variable(s) state for the state of \(M\). Specifically, since the state of a Turing machine is not in \(\{0,1\}\) but rather in a larger set \([k]\), we will use \(\ceil{\log k}\) variables state_\(0\) , \(\ldots\), state_\(\ceil{\log k}-1\) variables to store the representation of the state. Similarly, to encode the larger alphabet \(\Sigma\) of the tape, we will use \(\ceil{\log |\Sigma|}\) arrays Tape_\(0\) , \(\ldots\), Tape_\(\ceil{\log |\Sigma|}-1\), such that the \(i^{th}\) location of these arrays encodes the \(i^{th}\) symbol in the tape for every tape. Using the fact that every function can be computed by a NAND-CIRC program, we will be able to compute the transition function of \(M\), replacing moving left and right by decrementing and incrementing i respectively.
We show (2) using very similar ideas. Given a program \(P\) that uses \(a\) array variables and \(b\) scalar variables, we will create a Turing machine with about \(2^b\) states to encode the values of scalar variables, and an alphabet of about \(2^a\) so we can encode the arrays using our tape. (The reason the sizes are only “about” \(2^a\) and \(2^b\) is that we need to add some symbols and steps for bookkeeping purposes.) The Turing machine \(M\) simulates each iteration of the program \(P\) by updating its state and tape accordingly.
i for a NAND-TM program.We start by proving the “if” direction of Theorem 7.11. Namely we show that given a Turing machine \(M\), we can find a NAND-TM program \(P_M\) such that for every input \(x\), if \(M\) halts on input \(x\) with output \(y\) then \(P_M(x)=y\). Since our goal is just to show such a program \(P_M\) exists, we don’t need to write out the full code of \(P_M\) line by line, and can take advantage of our various “syntactic sugar” in describing it.
The key observation is that by Theorem 4.12 we can compute every finite function using a NAND-CIRC program. In particular, consider the transition function \(\delta_M:[k]\times \Sigma \rightarrow [k] \times \Sigma \times \{\mathsf{L},\mathsf{R},\mathsf{S},\mathsf{H}\}\) of our Turing machine. We can encode its components as follows:
We encode \([k]\) using \(\{0,1\}^\ell\) and \(\Sigma\) using \(\{0,1\}^{\ell'}\), where \(\ell = \ceil{\log k}\) and \(\ell' = \ceil{\log |\Sigma|}\).
We encode the set \(\{\mathsf{L},\mathsf{R}, \mathsf{S},\mathsf{H} \}\) using \(\{0,1\}^2\). We will choose the encoding \(\mathsf{L} \mapsto 01\), \(\mathsf{R} \mapsto 11\), \(\mathsf{S} \mapsto 10\), \(\mathsf{H} \mapsto 00\). (This conveniently corresponds to the semantics of the
MODANDJUMPoperation.)
Hence we can identify \(\delta_M\) with a function \(\overline{M}:\{0,1\}^{\ell+\ell'} \rightarrow \{0,1\}^{\ell+\ell'+2}\), mapping strings of length \(\ell+\ell'\) to strings of length \(\ell+\ell'+2\). By Theorem 4.12 there exists a finite length NAND-CIRC program ComputeM that computes this function \(\overline{M}\). The idea behind the NAND-TM program to simulate \(M\) is to:
Use variables
state_\(0\) \(\ldots\)state_\(\ell-1\) to encode \(M\)’s state.Use arrays
Tape_\(0\)[]\(\ldots\)Tape_\(\ell'-1\)[]to encode \(M\)’s tape.Use the fact that transition is finite and computable by NAND-CIRC program.
Given the above, we can write code of the form:
state_\(0\) \(\ldots\) state_\(\ell-1\), Tape_\(0\)[i]\(\ldots\) Tape_\(\ell'-1\)[i], dir0,dir1 \(\leftarrow\) TRANSITION( state_\(0\) \(\ldots\) state_\(\ell-1\), Tape_\(0\)[i]\(\ldots\) Tape_\(\ell'-1\)[i] )
MODANDJUMP(dir0,dir1)
Every step of the main loop of the above program perfectly mimics the computation of the Turing machine \(M\), and so the program carries out exactly the definition of computation by a Turing machine as per Definition 7.1.
For the other direction, suppose that \(P\) is a NAND-TM program with \(s\) lines, \(\ell\) scalar variables, and \(\ell'\) array variables. We will show that there exists a Turing machine \(M_P\) with \(2^\ell+C\) states and alphabet \(\Sigma\) of size \(C' + 2^{\ell'}\) that computes the same functions as \(P\) (where \(C\), \(C'\) are some constants to be determined later).
Specifically, consider the function \(\overline{P}:\{0,1\}^\ell \times \{0,1\}^{\ell'} \rightarrow \{0,1\}^\ell \times \{0,1\}^{\ell'}\) that on input the contents of \(P\)’s scalar variables and the contents of the array variables at location i in the beginning of an iteration, outputs all the new values of these variables at the last line of the iteration, right before the MODANDJUMP instruction is executed.
If foo and bar are the two variables that are used as input to the MODANDJUMP instruction, then based on the values of these variables we can compute whether i will increase, decrease or stay the same, and whether the program will halt or jump back to the beginning. Hence a Turing machine can simulate an execution of \(P\) in one iteration using a finite function applied to its alphabet. The overall operation of the Turing machine will be as follows:
The machine \(M_P\) encodes the contents of the array variables of \(P\) in its tape and the contents of the scalar variables in (part of) its state. Specifically, if \(P\) has \(\ell\) local variables and \(t\) arrays, then the state space of \(M\) will be large enough to encode all \(2^\ell\) assignments to the local variables, and the alphabet \(\Sigma\) of \(M\) will be large enough to encode all \(2^t\) assignments for the array variables at each location. The head location corresponds to the index variable
i.Recall that every line of the program \(P\) corresponds to reading and writing either a scalar variable, or an array variable at the location
i. In one iteration of \(P\) the value ofiremains fixed, and so the machine \(M\) can simulate this iteration by reading the values of all array variables ati(which are encoded by the single symbol in the alphabet \(\Sigma\) located at thei-th cell of the tape) , reading the values of all scalar variables (which are encoded by the state), and updating both. The transition function of \(M\) can output \(\mathsf{L},\mathsf{S},\mathsf{R}\) depending on whether the values given to theMODANDJUMPoperation are \(01\), \(10\) or \(11\) respectively.When the program halts (i.e.,
MODANDJUMPgets \(00\)) then the Turing machine will enter into a special loop to copy the results of theYarray into the output and then halt. We can achieve this by adding a few more states.
The above is not a full formal description of a Turing machine, but our goal is just to show that such a machine exists. One can see that \(M_P\) simulates every step of \(P\), and hence computes the same function as \(P\).
If we examine the proof of Theorem 7.11 then we can see that every iteration of the loop of a NAND-TM program corresponds to one step in the execution of the Turing machine. We will come back to this question of measuring the number of computation steps later in this course. For now, the main take away point is that NAND-TM programs and Turing machines are essentially equivalent in power even when taking running time into account.
Specification vs implementation (again)
Once you understand the definitions of both NAND-TM programs and Turing machines, Theorem 7.11 is straightforward. Indeed, NAND-TM programs are not as much a different model from Turing machines as they are simply a reformulation of the same model using programming language notation. You can think of the difference between a Turing machine and a NAND-TM program as the difference between representing a number using decimal or binary notation. In contrast, the difference between a function \(F\) and a Turing machine that computes \(F\) is much more profound: it is like the difference between the equation \(x^2 + x = 12\), and the number \(3\) that is a solution for this equation. For this reason, while we take special care in distinguishing functions from programs or machines, we will often identify the two latter concepts. We will move freely between describing an algorithm as a Turing machine or as a NAND-TM program (as well as some of the other equivalent computational models we will see in Chapter 8 and beyond).
Setting |
Specification |
Implementation |
|---|---|---|
Finite computation |
Functions mapping \(\{0,1\}^n\) to \(\{0,1\}^m\) |
Circuits, Straightline programs |
Infinite computation |
Functions mapping \(\{0,1\}^*\) to \(\{0,1\}\) or to \(\{0,1\}^*\). |
Algorithms, Turing Machines, Programs |
NAND-TM syntactic sugar
Just like we did with NAND-CIRC in Chapter 4, we can use “syntactic sugar” to make NAND-TM programs easier to write. For starters, we can use all of the syntactic sugar of NAND-CIRC, such as macro definitions and conditionals (i.e., if/then). However, we can go beyond this and achieve (for example):
Inner loops such as the
whileandforoperations common to many programming languages.Multiple index variables (e.g., not just
ibut we can addj,k, etc.).Arrays with more than one dimension (e.g.,
Foo[i][j],Bar[i][j][k]etc.)
In all of these cases (and many others) we can implement the new feature as mere “syntactic sugar” on top of standard NAND-TM. This means that the set of functions computable by NAND-TM with this feature is the same as the set of functions computable by standard NAND-TM. Similarly, we can show that the set of functions computable by Turing machines that have more than one tape, or tapes of more dimensions than one, is the same as the set of functions computable by standard Turing machines.
“GOTO” and inner loops
We can implement more advanced looping constructs than the simple MODANDJUMP. For example, we can implement GOTO. A GOTO statement corresponds to jumping to a specific line in the execution. For example, if we have code of the form
then the program will only do foo and blah as when it reaches the line GOTO("end") it will jump to the line labeled with "end". We can achieve the effect of GOTO in NAND-TM using conditionals. In the code below, we assume that we have a variable pc that can take strings of some constant length. This can be encoded using a finite number of Boolean variables pc_0, pc_1, \(\ldots\), pc_\(k-1\), and so when we write below pc = "label" what we mean is something like pc_0 = 0,pc_1 = 1, \(\ldots\) (where the bits \(0,1,\ldots\) correspond to the encoding of the finite string "label" as a string of length \(k\)). We also assume that we have access to conditional (i.e., if statements), which we can emulate using syntactic sugar in the same way as we did in NAND-CIRC.
To emulate a GOTO statement, we will first modify a program P of the form
to have the following form (using syntactic sugar for if):
pc = "line1"
if (pc=="line1"):
do foo
pc = "line2"
if (pc=="line2"):
do bar
pc = "line3"
if (pc=="line3"):
do blahThese two programs do the same thing. The variable pc corresponds to the “program counter” and tells the program which line to execute next. We can see that if we wanted to emulate a GOTO("line3") then we could simply modify the instruction pc = "line2" to be pc = "line3".
In NAND-CIRC we could only have GOTOs that go forward in the code, but since in NAND-TM everything is encompassed within a large outer loop, we can use the same ideas to implement GOTOs that can go backward, as well as conditional loops.
Other loops. Once we have GOTO, we can emulate all the standard loop constructs such as while, do .. until or for in NAND-TM as well. For example, we can replace the code
with
The GOTO statement was a staple of most early programming languages, but has largely fallen out of favor and is not included in many modern languages such as Python, Java, Javascript. In 1968, Edsger Dijsktra wrote a famous letter titled “Go to statement considered harmful.” (see also Figure 7.10). The main trouble with GOTO is that it makes analysis of programs more difficult by making it harder to argue about invariants of the program.
When a program contains a loop of the form:
you know that the line of code do blah can only be reached if the loop ended, in which case you know that j is equal to \(100\), and might also be able to argue other properties of the state of the program. In contrast, if the program might jump to do blah from any other point in the code, then it’s very hard for you as the programmer to know what you can rely upon in this code. As Dijkstra said, such invariants are important because _ “our intellectual powers are rather geared to master static relations and .. our powers to visualize processes evolving in time are relatively poorly developed”_ and so " we should … do …our utmost best to shorten the conceptual gap between the static program and the dynamic process."
That said, GOTO is still a major part of lower level languages where it is used to implement higher-level looping constructs such as while and for loops. For example, even though Java doesn’t have a GOTO statement, the Java Bytecode (which is a lower-level representation of Java) does have such a statement. Similarly, Python bytecode has instructions such as POP_JUMP_IF_TRUE that implement the GOTO functionality, and similar instructions are included in many assembly languages. The way we use GOTO to implement a higher-level functionality in NAND-TM is reminiscent of the way these various jump instructions are used to implement higher-level looping constructs.

GOTO statement.Uniformity, and NAND vs NAND-TM (discussion)
While NAND-TM adds extra operations over NAND-CIRC, it is not exactly accurate to say that NAND-TM programs or Turing machines are “more powerful” than NAND-CIRC programs or Boolean circuits. NAND-CIRC programs, having no loops, are simply not applicable for computing functions with an unbounded number of inputs. Thus, to compute a function \(F:\{0,1\}^* :\rightarrow \{0,1\}^*\) using NAND-CIRC (or equivalently, Boolean circuits) we need a collection of programs/circuits: one for every input length.
The key difference between NAND-CIRC and NAND-TM is that NAND-TM allows us to express the fact that the algorithm for computing parities of length-\(100\) strings is really the same one as the algorithm for computing parities of length-\(5\) strings (or similarly the fact that the algorithm for adding \(n\)-bit numbers is the same for every \(n\), etc.). That is, one can think of the NAND-TM program for general parity as the “seed” out of which we can grow NAND-CIRC programs for length \(10\), length \(100\), or length \(1000\) parities as needed.
This notion of a single algorithm that can compute functions of all input lengths is known as uniformity of computation. Hence we think of Turing machines / NAND-TM as uniform models of computation, as opposed to Boolean circuits or NAND-CIRC, which are non-uniform models, in which we have to specify a different program for every input length.
Looking ahead, we will see that this uniformity leads to another crucial difference between Turing machines and circuits. Turing machines can have inputs and outputs that are longer than the description of the machine as a string, and in particular there exists a Turing machine that can “self replicate” in the sense that it can print its own code. The notion of “self replication”, and the related notion of “self reference” are crucial to many aspects of computation, and beyond that to life itself, whether in the form of digital or biological programs.
For now, what you ought to remember is the following differences between uniform and non-uniform computational models:
Non-uniform computational models: Examples are NAND-CIRC programs and Boolean circuits. These are models where each individual program/circuit can compute a finite function \(f:\{0,1\}^n \rightarrow \{0,1\}^m\). We have seen that every finite function can be computed by some program/circuit. To discuss computation of an infinite function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\) we need to allow a sequence \(\{ P_n \}_{n\in \N}\) of programs/circuits (one for every input length), but this does not capture the notion of a single algorithm to compute the function \(F\).
Uniform computational models: Examples are Turing machines and NAND-TM programs. These are models where a single program/machine can take inputs of arbitrary length and hence compute an infinite function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\). The number of steps that a program/machine takes on some input is not a priori bounded in advance and in particular there is a chance that it will enter into an infinite loop. Unlike the non-uniform case, we have not shown that every infinite function can be computed by some NAND-TM program/Turing machine. We will come back to this point in Chapter 9.
- Turing machines capture the notion of a single algorithm that can evaluate functions of every input length.
- They are equivalent to NAND-TM programs, which add loops and arrays to NAND-CIRC.
- Unlike NAND-CIRC or Boolean circuits, the number of steps that a Turing machine takes on a given input is not fixed in advance. In fact, a Turing machine or a NAND-TM program can enter into an infinite loop on certain inputs, and not halt at all.
Exercises
Produce the code of a (syntactic-sugar free) NAND-TM program \(P\) that computes the (unbounded input length) Majority function \(Maj:\{0,1\}^* \rightarrow \{0,1\}\) where for every \(x\in \{0,1\}^*\), \(Maj(x)=1\) if and only if \(\sum_{i=0}^{|x|} x_i > |x|/2\). We say “produce” rather than “write” because you do not have to write the code of \(P\) by hand, but rather can use the programming language of your choice to compute this code.
Prove that the following functions are computable. For all of these functions, you do not have to fully specify the Turing machine or the NAND-TM program that computes the function, but rather only prove that such a machine or program exists:
\(\ensuremath{\mathit{INC}}:\{0,1\}^* \rightarrow \{0,1\}^*\) which takes as input a representation of a natural number \(n\) and outputs the representation of \(n+1\).
\(\ensuremath{\mathit{ADD}}:\{0,1\}^* \rightarrow \{0,1\}^*\) which takes as input a representation of a pair of natural numbers \((n,m)\) and outputs the representation of \(n+m\).
\(\ensuremath{\mathit{MULT}}:\{0,1\}^* \rightarrow \{0,1\}^*\), which takes a representation of a pair of natural numbers \((n,m)\) and outputs the representation of \(n\dot m\).
\(\ensuremath{\mathit{SORT}}:\{0,1\}^* \rightarrow \{0,1\}^*\) which takes as input the representation of a list of natural numbers \((a_0,\ldots,a_{n-1})\) and returns its sorted version \((b_0,\ldots,b_{n-1})\) such that for every \(i\in [n]\) there is some \(j \in [n]\) with \(b_i=a_j\) and \(b_0 \leq b_1 \leq \cdots \leq b_{n-1}\).
Define NAND-TM’ to be the variant of NAND-TM where there are two index variables i and j. Arrays can be indexed by either i or j. The operation MODANDJUMP takes four variables \(a,b,c,d\) and uses the values of \(c,d\) to decide whether to increment j, decrement j or keep it in the same value (corresponding to \(01\), \(10\), and \(00\) respectively). Prove that for every function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), \(F\) is computable by a NAND-TM program if and only if \(F\) is computable by a NAND-TM’ program.
Define a two tape Turing machine to be a Turing machine which has two separate tapes and two separate heads. At every step, the transition function gets as input the location of the cells in the two tapes, and can decide whether to move each head independently. Prove that for every function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), \(F\) is computable by a standard Turing machine if and only if \(F\) is computable by a two-tape Turing machine.
Define NAND-TM" to be the variant of NAND-TM where just like NAND-TM’ defined in Exercise 7.3 there are two index variables i and j, but now the arrays are two dimensional and so we index an array Foo by Foo[i][j]. Prove that for every function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), \(F\) is computable by a NAND-TM program if and only if \(F\) is computable by a NAND-TM’’ program.
Define a two-dimensional Turing machine to be a Turing machine in which the tape is two dimensional. At every step the machine can move \(\mathsf{U}\)p, \(\mathsf{D}\)own, \(\mathsf{L}\)eft, \(\mathsf{R}\)ight, or \(\mathsf{S}\)tay. Prove that for every function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), \(F\) is computable by a standard Turing machine if and only if \(F\) is computable by a two-dimensional Turing machine.
Prove the following closure properties of the set \(\mathbf{R}\) defined in Definition 7.3:
If \(F \in \mathbf{R}\) then the function \(G(x) = 1 - F(x)\) is in \(\mathbf{R}\).
If \(F,G \in \mathbf{R}\) then the function \(H(x) = F(x) \vee G(x)\) is in \(\mathbf{R}\).
If \(F \in \mathbf{R}\) then the function \(F^*\) in in \(\mathbf{R}\) where \(F^*\) is defined as follows: \(F^*(x)=1\) iff there exist some strings \(w_0,\ldots,w_{k-1}\) such that \(x = w_0 w_1 \cdots w_{k-1}\) and \(F(w_i)=1\) for every \(i\in [k]\).
If \(F \in \mathbf{R}\) then the function
\[ G(x) = \begin{cases} \exists_{y \in \{0,1\}^{|x|}} F(xy) = 1 \\ 0 & \text{otherwise} \end{cases} \]is in \(\mathbf{R}\).
Define a Turing machine \(M\) to be oblivious if its head movements are independent of its input. That is, we say that \(M\) is oblivious if there exists an infinite sequence \(\ensuremath{\mathit{MOVE}} \in \{\mathsf{L},\mathsf{R}, \mathsf{S} \}^\infty\) such that for every \(x\in \{0,1\}^*\), the movements of \(M\) when given input \(x\) (up until the point it halts, if such point exists) are given by \(\ensuremath{\mathit{MOVE}}_0,\ensuremath{\mathit{MOVE}}_1,\ensuremath{\mathit{MOVE}}_2,\ldots\).
Prove that for every function \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), if \(F\) is computable then it is computable by an oblivious Turing machine. See footnote for hint.3
Prove that for every \(F:\{0,1\}^* \rightarrow \{0,1\}^*\), the function \(F\) is computable if and only if the following function \(G:\{0,1\}^* \rightarrow \{0,1\}\) is computable, where \(G\) is defined as follows: \(G(x,i,\sigma) = \begin{cases} F(x)_i & i < |F(x)|, \sigma =0 \\ 1 & i < |F(x)|, \sigma = 1 \\ 0 & i \geq |F(x)| \end{cases}\)
Recall that \(\mathbf{R}\) is the set of all total functions from \(\{0,1\}^*\) to \(\{0,1\}\) that are computable by a Turing machine (see Definition 7.3). Prove that \(\mathbf{R}\) is countable. That is, prove that there exists a one-to-one map \(DtN:\mathbf{R} \rightarrow \mathbb{N}\). You can use the equivalence between Turing machines and NAND-TM programs.
Prove that the set of all total functions from \(\{0,1\}^* \rightarrow \{0,1\}\) is not countable. You can use the results of Section 2.4. (We will see an explicit uncomputable function in Chapter 9.)
Bibliographical notes
Augusta Ada Byron, countess of Lovelace (1815-1852) lived a short but turbulent life, though is today most well known for her collaboration with Charles Babbage (see (Stein, 1987) for a biography). Ada took an immense interest in Babbage’s analytical engine, which we mentioned in Chapter 3. In 1842-3, she translated from Italian a paper of Menabrea on the engine, adding copious notes (longer than the paper itself). The quote in the chapter’s beginning is taken from Nota A in this text. Lovelace’s notes contain several examples of programs for the analytical engine, and because of this she has been called “the world’s first computer programmer” though it is not clear whether they were written by Lovelace or Babbage himself (Holt, 2001) . Regardless, Ada was clearly one of very few people (perhaps the only one outside of Babbage himself) to fully appreciate how important and revolutionary the idea of mechanizing computation truly is.
The books of Shetterly (Shetterly, 2016) and Sobel (Sobel, 2017) discuss the history of human computers (who were female, more often than not) and their important contributions to scientific discoveries in astronomy and space exploration.
Alan Turing was one of the intellectual giants of the 20th century. He was not only the first person to define the notion of computation, but also invented and used some of the world’s earliest computational devices as part of the effort to break the Enigma cipher during World War II, saving millions of lives. Tragically, Turing committed suicide in 1954, following his conviction in 1952 for homosexual acts and a court-mandated hormonal treatment. In 2009, British prime minister Gordon Brown made an official public apology to Turing, and in 2013 Queen Elizabeth II granted Turing a posthumous pardon. Turing’s life is the subject of a great book and a mediocre movie.
Sipser’s text (Sipser, 1997) defines a Turing machine as a seven tuple consisting of the state space, input alphabet, tape alphabet, transition function, starting state, accepting state, and rejecting state. Superficially this looks like a very different definition than Definition 7.1 but it is simply a different representation of the same concept, just as a graph can be represented in either adjacency list or adjacency matrix form.
One difference is that Sipser considers a general set of states \(Q\) that is not necessarily of the form \(Q=\{0,1,2,\ldots, k-1\}\) for some natural number \(k>0\). Sipser also restricts his attention to Turing machines that output only a single bit and therefore designates two special halting states: the “\(0\) halting state” (often known as the rejecting state) and the other as the “\(1\) halting state” (often known as the accepting state). Thus instead of writing \(0\) or \(1\) on an output tape, the machine will enter into one of these states and halt. This again makes no difference to the computational power, though we prefer to consider the more general model of multi-bit outputs. (Sipser presents the basic task of a Turing machine as that of deciding a language as opposed to computing a function, but these are equivalent, see Remark 7.4.)
Sipser considers also functions with input in \(\Sigma^*\) for an arbitrary alphabet \(\Sigma\) (and hence distinguishes between the input alphabet which he denotes as \(\Sigma\) and the tape alphabet which he denotes as \(\Gamma\)), while we restrict attention to functions with binary strings as input. Again this is not a major issue, since we can always encode an element of \(\Sigma\) using a binary string of length \(\log \ceil{|\Sigma|}\). Finally (and this is a very minor point) Sipser requires the machine to either move left or right in every step, without the \(\mathsf{S}\)tay operation, though staying in place is very easy to emulate by simply moving right and then back left.
Another definition used in the literature is that a Turing machine \(M\) recognizes a language \(L\) if for every \(x\in L\), \(M(x)=1\) and for every \(x\not\in L\), \(M(x) \in \{0,\bot \}\). A language \(L\) is recursively enumerable if there exists a Turing machine \(M\) that recognizes it, and the set of all recursively enumerable languages is often denoted by \(\mathbf{RE}\). We will not use this terminology in this book.
One of the first programming-language formulations of Turing machines was given by Wang (Wang, 1957) . Our formulation of NAND-TM is aimed at making the connection with circuits more direct, with the eventual goal of using it for the Cook-Levin Theorem, as well as results such as \(\mathbf{P} \subseteq \mathbf{P_{/poly}}\) and \(\mathbf{BPP} \subseteq \mathbf{P_{/poly}}\). The website esolangs.org features a large variety of esoteric Turing-complete programming languages. One of the most famous of them is Brainf*ck.
- ↩
A partial function \(F\) from a set \(A\) to a set \(B\) is a function that is only defined on a subset of \(A\), (see Section 1.4.3). We can also think of such a function as mapping \(A\) to \(B \cup \{ \bot \}\) where \(\bot\) is a special “failure” symbol such that \(F(a)=\bot\) indicates the function \(F\) is not defined on \(a\).
- ↩
Most programming languages use arrays of fixed size, while a Turing machine’s tape is unbounded. But of course there is no need to store an infinite number of \(\varnothing\) symbols. If you want, you can think of the tape as a list that starts off just long enough to store the input, but is dynamically grown in size as the Turing machine’s head explores new positions.
- ↩
You can use the sequence \(\mathsf{R}\), \(\mathsf{L}\),\(\mathsf{R}\), \(\mathsf{R}\), \(\mathsf{L}\), \(\mathsf{L}\), \(\mathsf{R}\),\(\mathsf{R}\),\(\mathsf{R}\), \(\mathsf{L}\), \(\mathsf{L}\), \(\mathsf{L}\), \(\ldots\).
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 12/06/2023 00:07:28
Copyright 2023, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.