See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
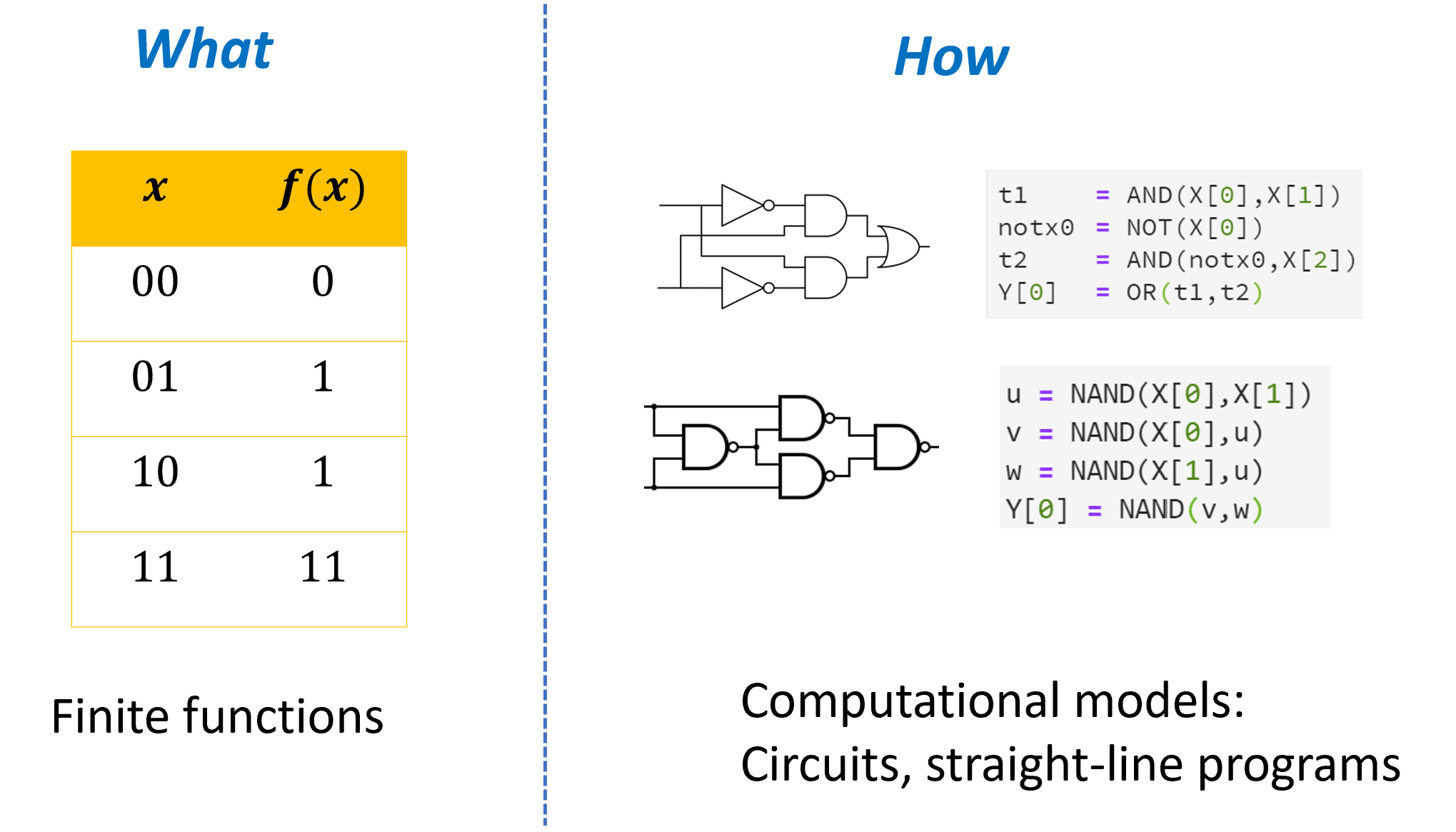
Defining computation
- See that computation can be precisely modeled.
- Learn the computational model of Boolean circuits / straight-line programs.
- Equivalence of circuits and straight-line programs.
- Equivalence of AND/OR/NOT and NAND.
- Examples of computing in the physical world.
“there is no reason why mental as well as bodily labor should not be economized by the aid of machinery”, Charles Babbage, 1852
“If, unwarned by my example, any man shall undertake and shall succeed in constructing an engine embodying in itself the whole of the executive department of mathematical analysis upon different principles or by simpler mechanical means, I have no fear of leaving my reputation in his charge, for he alone will be fully able to appreciate the nature of my efforts and the value of their results.”, Charles Babbage, 1864
“To understand a program you must become both the machine and the program.”, Alan Perlis, 1982


People have been computing for thousands of years, with aids that include not just pen and paper, but also abacus, slide rules, various mechanical devices, and modern electronic computers. A priori, the notion of computation seems to be tied to the particular mechanism that you use. You might think that the “best” algorithm for multiplying numbers will differ if you implement it in Python on a modern laptop than if you use pen and paper. However, as we saw in the introduction (Chapter 0), an algorithm that is asymptotically better would eventually beat a worse one regardless of the underlying technology. This gives us hope for a technology independent way of defining computation. This is what we do in this chapter. We will define the notion of computing an output from an input by applying a sequence of basic operations (see Figure 3.3). Using this, we will be able to precisely define statements such as “function \(f\) can be computed by model \(X\)” or “function \(f\) can be computed by model \(X\) using \(s\) operations”.
The main takeaways from this chapter are:
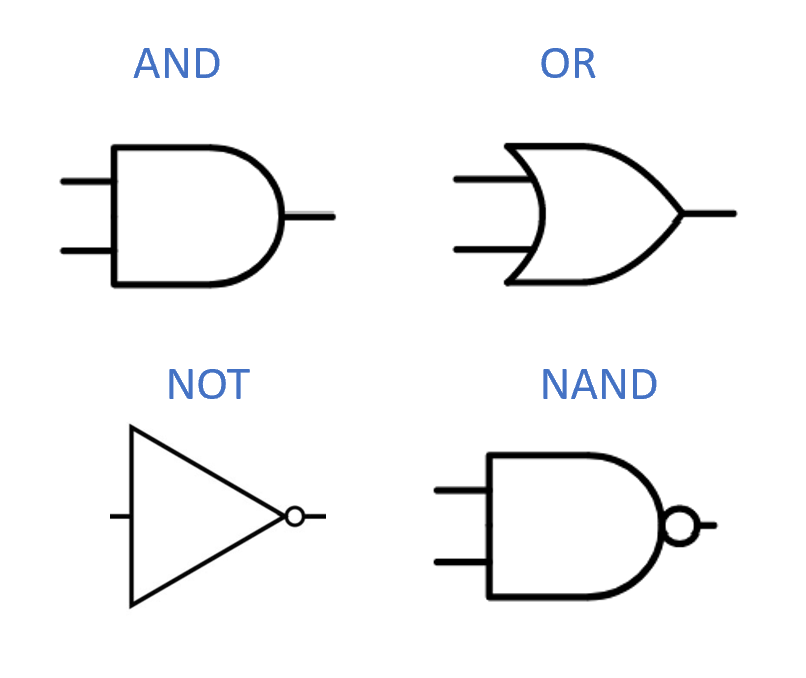
We can use logical operations such as \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\) to compute an output from an input (see Section 3.2).
A Boolean circuit is a way to compose the basic logical operations to compute a more complex function (see Section 3.3). We can think of Boolean circuits as both a mathematical model (which is based on directed acyclic graphs) as well as physical devices we can construct in the real world in a variety of ways, including not just silicon-based semi-conductors but also mechanical and even biological mechanisms (see Section 3.5).
We can describe Boolean circuits also as straight-line programs, which are programs that do not have any looping constructs (i.e., no
while/for/do .. untiletc.), see Section 3.4.It is possible to implement the \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\) operations using the \(\ensuremath{\mathit{NAND}}\) operation (as well as vice versa). This means that circuits with \(\ensuremath{\mathit{AND}}\)/\(\ensuremath{\mathit{OR}}\)/\(\ensuremath{\mathit{NOT}}\) gates can compute the same functions (i.e., are equivalent in power) to circuits with \(\ensuremath{\mathit{NAND}}\) gates, and we can use either model to describe computation based on our convenience, see Section 3.6. To give out a “spoiler”, we will see in Chapter 4 that such circuits can compute all finite functions.
One “big idea” of this chapter is the notion of equivalence between models (Big Idea 3). Two computational models are equivalent if they can compute the same set of functions. Boolean circuits with \(\ensuremath{\mathit{AND}}\)/\(\ensuremath{\mathit{OR}}\)/\(\ensuremath{\mathit{NOT}}\) gates are equivalent to circuits with \(\ensuremath{\mathit{NAND}}\) gates, but this is just one example of the more general phenomenon that we will see many times in this book.
Defining computation
The name “algorithm” is derived from the Latin transliteration of Muhammad ibn Musa al-Khwarizmi’s name. Al-Khwarizmi was a Persian scholar during the 9th century whose books introduced the western world to the decimal positional numeral system, as well as to the solutions of linear and quadratic equations (see Figure 3.4). However Al-Khwarizmi’s descriptions of algorithms were rather informal by today’s standards. Rather than use “variables” such as \(x,y\), he used concrete numbers such as 10 and 39, and trusted the reader to be able to extrapolate from these examples, much as algorithms are still taught to children today.
Here is how Al-Khwarizmi described the algorithm for solving an equation of the form \(x^2 +bx = c\):
[How to solve an equation of the form ] “roots and squares are equal to numbers”: For instance “one square, and ten roots of the same, amount to thirty-nine dirhems” that is to say, what must be the square which, when increased by ten of its own root, amounts to thirty-nine? The solution is this: you halve the number of the roots, which in the present instance yields five. This you multiply by itself; the product is twenty-five. Add this to thirty-nine’ the sum is sixty-four. Now take the root of this, which is eight, and subtract from it half the number of roots, which is five; the remainder is three. This is the root of the square which you sought for; the square itself is nine.


For the purposes of this book, we will need a much more precise way to describe algorithms. Fortunately (or is it unfortunately?), at least at the moment, computers lag far behind school-age children in learning from examples. Hence in the 20th century, people came up with exact formalisms for describing algorithms, namely programming languages. Here is al-Khwarizmi’s quadratic equation solving algorithm described in the Python programming language:
from math import sqrt
#Pythonspeak to enable use of the sqrt function to compute square roots.
def solve_eq(b,c):
# return solution of x^2 + bx = c following Al Khwarizmi's instructions
# Al Kwarizmi demonstrates this for the case b=10 and c= 39
val1 = b / 2.0 # "halve the number of the roots"
val2 = val1 * val1 # "this you multiply by itself"
val3 = val2 + c # "Add this to thirty-nine"
val4 = sqrt(val3) # "take the root of this"
val5 = val4 - val1 # "subtract from it half the number of roots"
return val5 # "This is the root of the square which you sought for"
# Test: solve x^2 + 10*x = 39
print(solve_eq(10,39))
# 3.0We can define algorithms informally as follows:
Informal definition of an algorithm: An algorithm is a set of instructions for how to compute an output from an input by following a sequence of “elementary steps”.
An algorithm \(A\) computes a function \(F\) if for every input \(x\), if we follow the instructions of \(A\) on the input \(x\), we obtain the output \(F(x)\).
In this chapter we will make this informal definition precise using the model of Boolean Circuits. We will show that Boolean Circuits are equivalent in power to straight line programs that are written in “ultra simple” programming languages that do not even have loops. We will also see that the particular choice of elementary operations is immaterial and many different choices yield models with equivalent power (see Figure 3.6). However, it will take us some time to get there. We will start by discussing what are “elementary operations” and how we map a description of an algorithm into an actual physical process that produces an output from an input in the real world.
Computing using AND, OR, and NOT.
An algorithm breaks down a complex calculation into a series of simpler steps. These steps can be executed in a variety of different ways, including:
Writing down symbols on a piece of paper.
Modifying the current flowing on electrical wires.
Binding a protein to a strand of DNA.
Responding to a stimulus by a member of a collection (e.g., a bee in a colony, a trader in a market).
To formally define algorithms, let us try to “err on the side of simplicity” and model our “basic steps” as truly minimal. For example, here are some very simple functions:
- \(\ensuremath{\mathit{OR}}:\{0,1\}^2 \rightarrow \{0,1\}\) defined as
- \(\ensuremath{\mathit{AND}}:\{0,1\}^2 \rightarrow \{0,1\}\) defined as
- \(\ensuremath{\mathit{NOT}}:\{0,1\} \rightarrow \{0,1\}\) defined as
The functions \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) and \(\ensuremath{\mathit{NOT}}\), are the basic logical operators used in logic and many computer systems. In the context of logic, it is common to use the notation \(a \wedge b\) for \(\ensuremath{\mathit{AND}}(a,b)\), \(a \vee b\) for \(\ensuremath{\mathit{OR}}(a,b)\) and \(\overline{a}\) and \(\neg a\) for \(\ensuremath{\mathit{NOT}}(a)\), and we will use this notation as well.
Each one of the functions \(\ensuremath{\mathit{AND}},\ensuremath{\mathit{OR}},\ensuremath{\mathit{NOT}}\) takes either one or two single bits as input, and produces a single bit as output. Clearly, it cannot get much more basic than that. However, the power of computation comes from composing such simple building blocks together.
Consider the function \(\ensuremath{\mathit{MAJ}}:\{0,1\}^3 \rightarrow \{0,1\}\) that is defined as follows:
That is, for every \(x\in \{0,1\}^3\), \(\ensuremath{\mathit{MAJ}}(x)=1\) if and only if the majority (i.e., at least two out of the three) of \(x\)’s elements are equal to \(1\). Can you come up with a formula involving \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) and \(\ensuremath{\mathit{NOT}}\) to compute \(\ensuremath{\mathit{MAJ}}\)? (It would be useful for you to pause at this point and work out the formula for yourself. As a hint, although the \(\ensuremath{\mathit{NOT}}\) operator is needed to compute some functions, you will not need to use it to compute \(\ensuremath{\mathit{MAJ}}\).)
Let us first try to rephrase \(\ensuremath{\mathit{MAJ}}(x)\) in words: “\(\ensuremath{\mathit{MAJ}}(x)=1\) if and only if there exists some pair of distinct elements \(i,j\) such that both \(x_i\) and \(x_j\) are equal to \(1\).” In other words it means that \(\ensuremath{\mathit{MAJ}}(x)=1\) iff either both \(x_0=1\) and \(x_1=1\), or both \(x_1=1\) and \(x_2=1\), or both \(x_0=1\) and \(x_2=1\). Since the \(\ensuremath{\mathit{OR}}\) of three conditions \(c_0,c_1,c_2\) can be written as \(\ensuremath{\mathit{OR}}(c_0,\ensuremath{\mathit{OR}}(c_1,c_2))\), we can now translate this into a formula as follows:
Recall that we can also write \(a \vee b\) for \(\ensuremath{\mathit{OR}}(a,b)\) and \(a \wedge b\) for \(\ensuremath{\mathit{AND}}(a,b)\). With this notation, Equation 3.1 can also be written as
We can also write Equation 3.1 in a “programming language” form, expressing it as a set of instructions for computing \(\ensuremath{\mathit{MAJ}}\) given the basic operations \(\ensuremath{\mathit{AND}},\ensuremath{\mathit{OR}},\ensuremath{\mathit{NOT}}\):
Some properties of AND and OR
Like standard addition and multiplication, the functions \(\ensuremath{\mathit{AND}}\) and \(\ensuremath{\mathit{OR}}\) satisfy the properties of commutativity: \(a \vee b = b \vee a\) and \(a \wedge b = b \wedge a\) and associativity: \((a \vee b) \vee c = a \vee (b \vee c)\) and \((a \wedge b) \wedge c = a \wedge (b \wedge c)\). As in the case of addition and multiplication, we often drop the parenthesis and write \(a \vee b \vee c \vee d\) for \(((a \vee b) \vee c) \vee d\), and similarly OR’s and AND’s of more terms. They also satisfy a variant of the distributive law:
Prove that for every \(a,b,c \in \{0,1\}\), \(a \wedge (b \vee c) = (a \wedge b) \vee (a \wedge c)\).
We can prove this by enumerating over all the \(8\) possible values for \(a,b,c \in \{0,1\}\) but it also follows from the standard distributive law. Suppose that we identify any positive integer with “true” and the value zero with “false”. Then for every numbers \(u,v \in \N\), \(u+v\) is positive if and only if \(u \vee v\) is true and \(u \cdot v\) is positive if and only if \(u \wedge v\) is true. This means that for every \(a,b,c \in \{0,1\}\), the expression \(a \wedge (b \vee c)\) is true if and only if \(a \cdot(b+c)\) is positive, and the expression \((a \wedge b) \vee (a \wedge c)\) is true if and only if \(a \cdot b + a \cdot c\) is positive, But by the standard distributive law \(a\cdot (b+c) = a\cdot b + a \cdot c\) and hence the former expression is true if and only if the latter one is.
Extended example: Computing \(\ensuremath{\mathit{XOR}}\) from \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\)
Let us see how we can obtain a different function from the same building blocks. Define \(\ensuremath{\mathit{XOR}}:\{0,1\}^2 \rightarrow \{0,1\}\) to be the function \(\ensuremath{\mathit{XOR}}(a,b)= a + b \mod 2\). That is, \(\ensuremath{\mathit{XOR}}(0,0)=\ensuremath{\mathit{XOR}}(1,1)=0\) and \(\ensuremath{\mathit{XOR}}(1,0)=\ensuremath{\mathit{XOR}}(0,1)=1\). We claim that we can construct \(\ensuremath{\mathit{XOR}}\) using only \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\).
As usual, it is a good exercise to try to work out the algorithm for \(\ensuremath{\mathit{XOR}}\) using \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) and \(\ensuremath{\mathit{NOT}}\) on your own before reading further.
The following algorithm computes \(\ensuremath{\mathit{XOR}}\) using \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\):
Algorithm 3.2 XOR from AND/OR/NOT
Input: \(a,b \in \{0,1\}\).
Output: \(XOR(a,b)\)
\(w1 \leftarrow AND(a,b)\)
\(w2 \leftarrow NOT(w1)\)
\(w3 \leftarrow OR(a,b)\)
return \(AND(w2,w3)\)
For every \(a,b\in \{0,1\}\), on input \(a,b\), Algorithm 3.2 outputs \(a+b \mod 2\).
For every \(a,b\), \(\ensuremath{\mathit{XOR}}(a,b)=1\) if and only if \(a\) is different from \(b\). On input \(a,b\in \{0,1\}\), Algorithm 3.2 outputs \(\ensuremath{\mathit{AND}}(w2,w3)\) where \(w2=\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{AND}}(a,b))\) and \(w3=\ensuremath{\mathit{OR}}(a,b)\).
If \(a=b=0\) then \(w3=\ensuremath{\mathit{OR}}(a,b)=0\) and so the output will be \(0\).
If \(a=b=1\) then \(\ensuremath{\mathit{AND}}(a,b)=1\) and so \(w2=\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{AND}}(a,b))=0\) and the output will be \(0\).
If \(a=1\) and \(b=0\) (or vice versa) then both \(w3=\ensuremath{\mathit{OR}}(a,b)=1\) and \(w1=\ensuremath{\mathit{AND}}(a,b)=0\), in which case the algorithm will output \(\ensuremath{\mathit{OR}}(\ensuremath{\mathit{NOT}}(w1),w3)=1\).
We can also express Algorithm 3.2 using a programming language. Specifically, the following is a Python program that computes the \(\ensuremath{\mathit{XOR}}\) function:
def AND(a,b): return a*b
def OR(a,b): return 1-(1-a)*(1-b)
def NOT(a): return 1-a
def XOR(a,b):
w1 = AND(a,b)
w2 = NOT(w1)
w3 = OR(a,b)
return AND(w2,w3)
# Test out the code
print([f"XOR({a},{b})={XOR(a,b)}" for a in [0,1] for b in [0,1]])
# ['XOR(0,0)=0', 'XOR(0,1)=1', 'XOR(1,0)=1', 'XOR(1,1)=0']Let \(\ensuremath{\mathit{XOR}}_3:\{0,1\}^3 \rightarrow \{0,1\}\) be the function defined as \(\ensuremath{\mathit{XOR}}_3(a,b,c) = a + b +c \mod 2\). That is, \(\ensuremath{\mathit{XOR}}_3(a,b,c)=1\) if \(a+b+c\) is odd, and \(\ensuremath{\mathit{XOR}}_3(a,b,c)=0\) otherwise. Show that you can compute \(\ensuremath{\mathit{XOR}}_3\) using AND, OR, and NOT. You can express it as a formula, use a programming language such as Python, or use a Boolean circuit.
Addition modulo two satisfies the same properties of associativity (\((a+b)+c=a+(b+c)\)) and commutativity (\(a+b=b+a\)) as standard addition. This means that, if we define \(a \oplus b\) to equal \(a + b \mod 2\), then
Since we know how to compute \(\ensuremath{\mathit{XOR}}\) using AND, OR, and NOT, we can compose this to compute \(\ensuremath{\mathit{XOR}}_3\) using the same building blocks. In Python this corresponds to the following program:
def XOR3(a,b,c):
w1 = AND(a,b)
w2 = NOT(w1)
w3 = OR(a,b)
w4 = AND(w2,w3)
w5 = AND(w4,c)
w6 = NOT(w5)
w7 = OR(w4,c)
return AND(w6,w7)
# Let's test this out
print([f"XOR3({a},{b},{c})={XOR3(a,b,c)}" for a in [0,1] for b in [0,1] for c in [0,1]])
# ['XOR3(0,0,0)=0', 'XOR3(0,0,1)=1', 'XOR3(0,1,0)=1', 'XOR3(0,1,1)=0', 'XOR3(1,0,0)=1', 'XOR3(1,0,1)=0', 'XOR3(1,1,0)=0', 'XOR3(1,1,1)=1']Try to generalize the above examples to obtain a way to compute \(\ensuremath{\mathit{XOR}}_n:\{0,1\}^n \rightarrow \{0,1\}\) for every \(n\) using at most \(4n\) basic steps involving applications of a function in \(\{ \ensuremath{\mathit{AND}}, \ensuremath{\mathit{OR}} , \ensuremath{\mathit{NOT}} \}\) to outputs or previously computed values.
Informally defining “basic operations” and “algorithms”
We have seen that we can obtain at least some examples of interesting functions by composing together applications of \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\). This suggests that we can use \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\) as our “basic operations”, hence obtaining the following definition of an “algorithm”:
Semi-formal definition of an algorithm: An algorithm consists of a sequence of steps of the form “compute a new value by applying \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), or \(\ensuremath{\mathit{NOT}}\) to previously computed values (assuming that the input was also previously computed)”.
An algorithm \(A\) computes a function \(F\) if for every input \(x\) to \(F\), if we feed \(x\) as input to the algorithm, the value computed in its last step is \(F(x)\).
There are several concerns that are raised by this definition:
First and foremost, this definition is indeed too informal. We do not specify exactly what each step does, nor what it means to “feed \(x\) as input”.
Second, the choice of \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) or \(\ensuremath{\mathit{NOT}}\) seems rather arbitrary. Why not \(\ensuremath{\mathit{XOR}}\) and \(\ensuremath{\mathit{MAJ}}\)? Why not allow operations like addition and multiplication? What about any other logical constructions such
if/thenorwhile?Third, do we even know that this definition has anything to do with actual computing? If someone gave us a description of such an algorithm, could we use it to actually compute the function in the real world?
These concerns will to a large extent guide us in the upcoming chapters. Thus you would be well advised to re-read the above informal definition and see what you think about these issues.
A large part of this book will be devoted to addressing the above issues. We will see that:
We can make the definition of an algorithm fully formal, and so give a precise mathematical meaning to statements such as “Algorithm \(A\) computes function \(f\)”.
While the choice of \(\ensuremath{\mathit{AND}}\)/\(\ensuremath{\mathit{OR}}\)/\(\ensuremath{\mathit{NOT}}\) is arbitrary, and we could just as well have chosen other functions, we will also see this choice does not matter much. We will see that we would obtain the same computational power if we instead used addition and multiplication, and essentially every other operation that could be reasonably thought of as a basic step.
It turns out that we can and do compute such “\(\ensuremath{\mathit{AND}}\)/\(\ensuremath{\mathit{OR}}\)/\(\ensuremath{\mathit{NOT}}\)-based algorithms” in the real world. First of all, such an algorithm is clearly well specified, and so can be executed by a human with a pen and paper. Second, there are a variety of ways to mechanize this computation. We’ve already seen that we can write Python code that corresponds to following such a list of instructions. But in fact we can directly implement operations such as \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\) via electronic signals using components known as transistors. This is how modern electronic computers operate.
In the remainder of this chapter, and the rest of this book, we will begin to answer some of these questions. We will see more examples of the power of simple operations to compute more complex operations including addition, multiplication, sorting and more. We will also discuss how to physically implement simple operations such as \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) and \(\ensuremath{\mathit{NOT}}\) using a variety of technologies.
Boolean Circuits
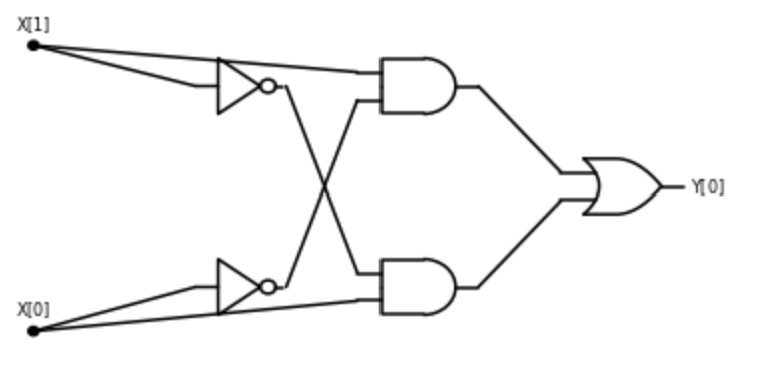
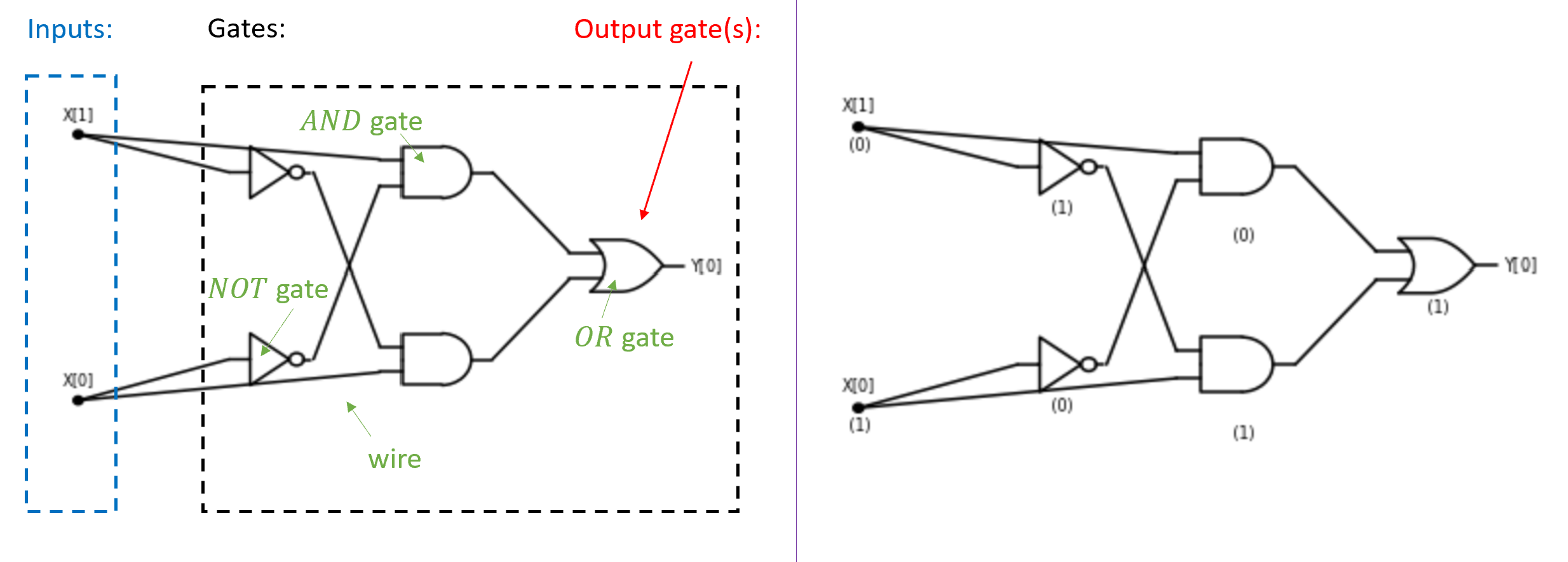
Boolean circuits provide a precise notion of “composing basic operations together”. A Boolean circuit (see Figure 3.9) is composed of gates and inputs that are connected by wires. The wires carry a signal that represents either the value \(0\) or \(1\). Each gate corresponds to either the OR, AND, or NOT operation. An OR gate has two incoming wires, and one or more outgoing wires. If these two incoming wires carry the signals \(a\) and \(b\) (for \(a,b \in \{0,1\}\)), then the signal on the outgoing wires will be \(\ensuremath{\mathit{OR}}(a,b)\). AND and NOT gates are defined similarly. The inputs have only outgoing wires. If we set a certain input to a value \(a\in \{0,1\}\), then this value is propagated on all the wires outgoing from it. We also designate some gates as output gates, and their value corresponds to the result of evaluating the circuit. For example, Figure 3.8 gives such a circuit for the \(\ensuremath{\mathit{XOR}}\) function, following Section 3.2.2. We evaluate an \(n\)-input Boolean circuit \(C\) on an input \(x\in \{0,1\}^n\) by placing the bits of \(x\) on the inputs, and then propagating the values on the wires until we reach an output, see Figure 3.9.
Boolean circuits are a mathematical model that does not necessarily correspond to a physical object, but they can be implemented physically. In physical implementations of circuits, the signal is often implemented by electric potential, or voltage, on a wire, where for example voltage above a certain level is interpreted as a logical value of \(1\), and below a certain level is interpreted as a logical value of \(0\). Section 3.5 discusses physical implementations of Boolean circuits (with examples including using electrical signals such as in silicon-based circuits, as well as biological and mechanical implementations).
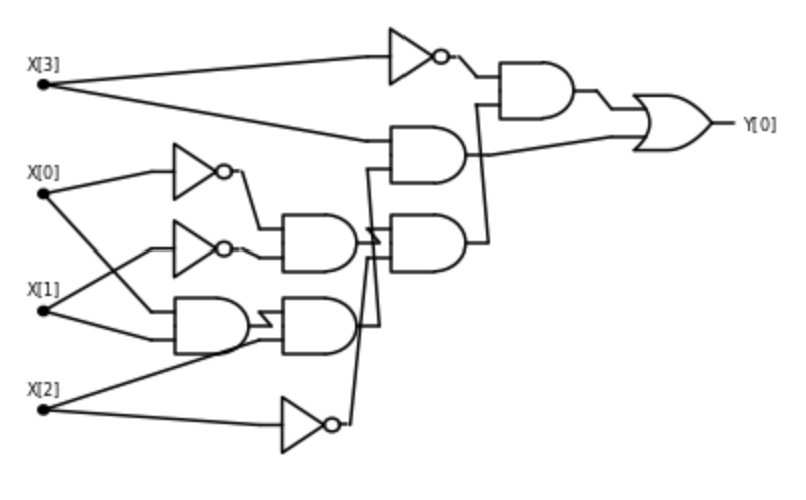
Define \(\ensuremath{\mathit{ALLEQ}}:\{0,1\}^4 \rightarrow \{0,1\}\) to be the function that on input \(x\in \{0,1\}^4\) outputs \(1\) if and only if \(x_0=x_1=x_2=x_3\). Give a Boolean circuit for computing \(\ensuremath{\mathit{ALLEQ}}\).
Another way to describe the function \(\ensuremath{\mathit{ALLEQ}}\) is that it outputs \(1\) on an input \(x\in \{0,1\}^4\) if and only if \(x = 0^4\) or \(x=1^4\). We can phrase the condition \(x=1^4\) as \(x_0 \wedge x_1 \wedge x_2 \wedge x_3\) which can be computed using three AND gates. Similarly we can phrase the condition \(x=0^4\) as \(\overline{x}_0 \wedge \overline{x}_1 \wedge \overline{x}_2 \wedge \overline{x}_3\) which can be computed using four NOT gates and three AND gates. The output of \(\ensuremath{\mathit{ALLEQ}}\) is the OR of these two conditions, which results in the circuit of 4 NOT gates, 6 AND gates, and one OR gate presented in Figure 3.10.
Boolean circuits: a formal definition
We defined Boolean circuits informally as obtained by connecting AND, OR, and NOT gates via wires so as to produce an output from an input. However, to be able to prove theorems about the existence or non-existence of Boolean circuits for computing various functions we need to:
Formally define a Boolean circuit as a mathematical object.
Formally define what it means for a circuit \(C\) to compute a function \(f\).
We now proceed to do so. We will define a Boolean circuit as a labeled Directed Acyclic Graph (DAG). The vertices of the graph correspond to the gates and inputs of the circuit, and the edges of the graph correspond to the wires. A wire from an input or gate \(u\) to a gate \(v\) in the circuit corresponds to a directed edge between the corresponding vertices. The inputs are vertices with no incoming edges, while each gate has the appropriate number of incoming edges based on the function it computes. (That is, AND and OR gates have two in-neighbors, while NOT gates have one in-neighbor.) The formal definition is as follows (see also Figure 3.11):
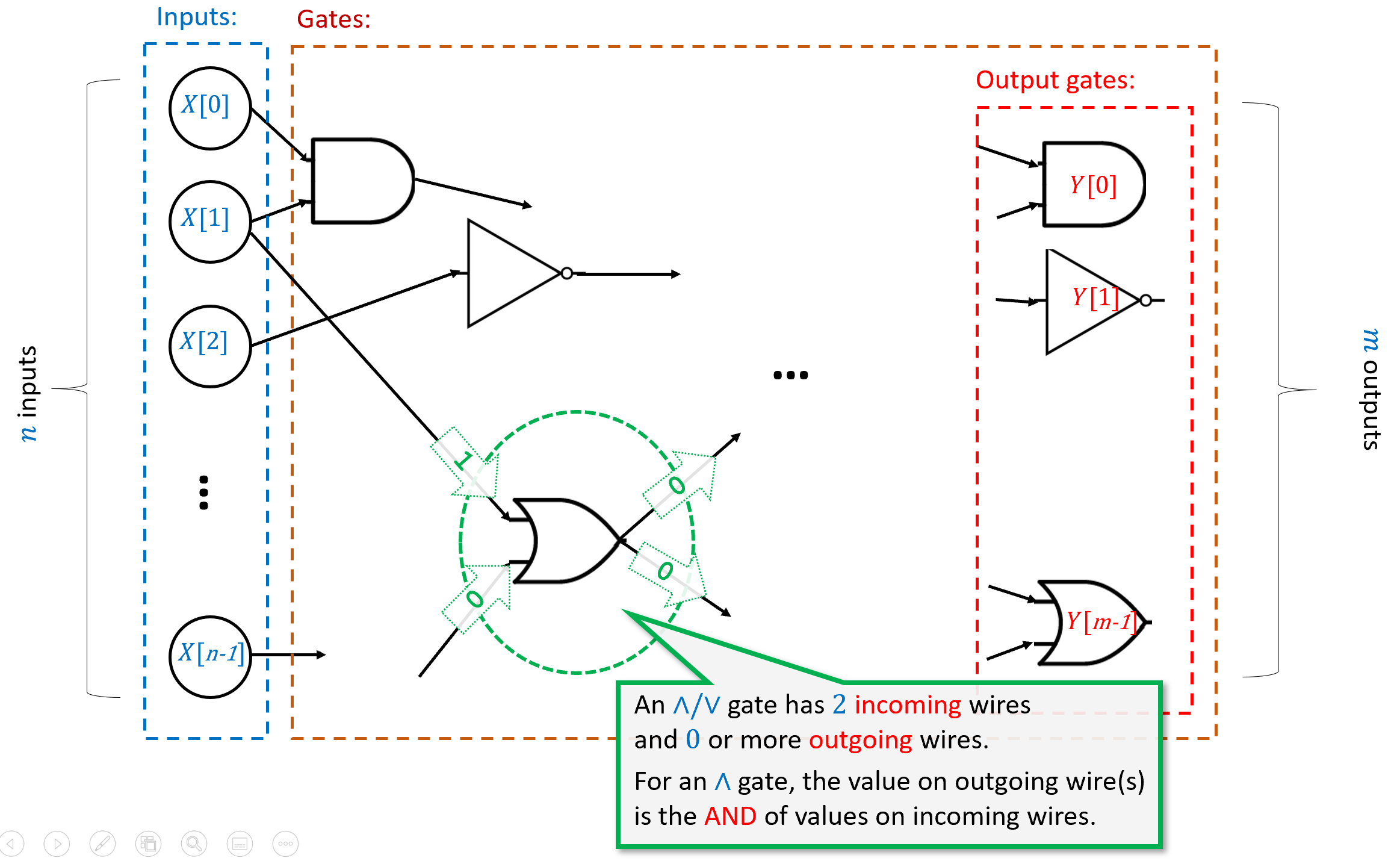
X[\(0\)],\(\ldots\), X[\(n-1\)] and have no incoming edges, and the rest of the vertices are gates. AND, OR, and NOT gates have two, two, and one incoming edges, respectively. If the circuit has \(m\) outputs, then \(m\) of the gates are known as outputs and are marked with Y[\(0\)],\(\ldots\),Y[\(m-1\)]. When we evaluate a circuit \(C\) on an input \(x\in \{0,1\}^n\), we start by setting the value of the input vertices to \(x_0,\ldots,x_{n-1}\) and then propagate the values, assigning to each gate \(g\) the result of applying the operation of \(g\) to the values of \(g\)’s in-neighbors. The output of the circuit is the value assigned to the output gates.Let \(n,m,s\) be positive integers with \(s \geq m\). A Boolean circuit with \(n\) inputs, \(m\) outputs, and \(s\) gates, is a labeled directed acyclic graph (DAG) \(G=(V,E)\) with \(s+n\) vertices satisfying the following properties:
Exactly \(n\) of the vertices have no in-neighbors. These vertices are known as inputs and are labeled with the \(n\) labels
X[\(0\)], \(\ldots\),X[\(n-1\)]. Each input has at least one out-neighbor.The other \(s\) vertices are known as gates. Each gate is labeled with \(\wedge\), \(\vee\) or \(\neg\). Gates labeled with \(\wedge\) (AND) or \(\vee\) (OR) have two in-neighbors. Gates labeled with \(\neg\) (NOT) have one in-neighbor. We will allow parallel edges.1
Exactly \(m\) of the gates are also labeled with the \(m\) labels
Y[\(0\)], \(\ldots\),Y[\(m-1\)](in addition to their label \(\wedge\)/\(\vee\)/\(\neg\)). These are known as outputs.
The size of a Boolean circuit is the number \(s\) of gates it contains.
This is a non-trivial mathematical definition, so it is worth taking the time to read it slowly and carefully. As in all mathematical definitions, we are using a known mathematical object — a directed acyclic graph (DAG) — to define a new object, a Boolean circuit. This might be a good time to review some of the basic properties of DAGs and in particular the fact that they can be topologically sorted, see Section 1.6.
If \(C\) is a circuit with \(n\) inputs and \(m\) outputs, and \(x\in \{0,1\}^n\), then we can compute the output of \(C\) on the input \(x\) in the natural way: assign the input vertices X[\(0\)], \(\ldots\), X[\(n-1\)] the values \(x_0,\ldots,x_{n-1}\), apply each gate on the values of its in-neighbors, and then output the values that correspond to the output vertices. Formally, this is defined as follows:
Let \(C\) be a Boolean circuit with \(n\) inputs and \(m\) outputs. For every \(x\in \{0,1\}^n\), the output of \(C\) on the input \(x\), denoted by \(C(x)\), is defined as the result of the following process:
We let \(h:V \rightarrow \N\) be the minimal layering of \(C\) (aka topological sorting, see Theorem 1.26). We let \(L\) be the maximum layer of \(h\), and for \(\ell=0,1,\ldots,L\) we do the following:
For every \(v\) in the \(\ell\)-th layer (i.e., \(v\) such that \(h(v)=\ell\)) do:
If \(v\) is an input vertex labeled with
X[\(i\)]for some \(i\in [n]\), then we assign to \(v\) the value \(x_i\).If \(v\) is a gate vertex labeled with \(\wedge\) and with two in-neighbors \(u,w\) then we assign to \(v\) the AND of the values assigned to \(u\) and \(w\). (Since \(u\) and \(w\) are in-neighbors of \(v\), they are in a lower layer than \(v\), and hence their values have already been assigned.)
If \(v\) is a gate vertex labeled with \(\vee\) and with two in-neighbors \(u,w\) then we assign to \(v\) the OR of the values assigned to \(u\) and \(w\).
If \(v\) is a gate vertex labeled with \(\neg\) and with one in-neighbor \(u\) then we assign to \(v\) the negation of the value assigned to \(u\).
The result of this process is the value \(y\in \{0,1\}^m\) such that for every \(j\in [m]\), \(y_j\) is the value assigned to the vertex with label
Y[\(j\)].
Let \(f:\{0,1\}^n \rightarrow \{0,1\}^m\). We say that the circuit \(C\) computes \(f\) if for every \(x\in \{0,1\}^n\), \(C(x)=f(x)\).
In phrasing Definition 3.5, we’ve made some technical choices that are not very important, but will be convenient for us later on. Having parallel edges means an AND or OR gate \(u\) can have both its in-neighbors be the same gate \(v\). Since \(\ensuremath{\mathit{AND}}(a,a)=\ensuremath{\mathit{OR}}(a,a)=a\) for every \(a\in \{0,1\}\), such parallel edges don’t help in computing new values in circuits with AND/OR/NOT gates. However, we will see circuits with more general sets of gates later on. The condition that every input vertex has at least one out-neighbor is also not very important because we can always add “dummy gates” that touch these inputs. However, it is convenient since it guarantees that (since every gate has at most two in-neighbors) the number of inputs in a circuit is never larger than twice its size.
Straight-line programs
We have seen two ways to describe how to compute a function \(f\) using AND, OR and NOT:
A Boolean circuit, defined in Definition 3.5, computes \(f\) by connecting via wires AND, OR, and NOT gates to the inputs.
We can also describe such a computation using a straight-line program that has lines of the form
foo = AND(bar,blah),foo = OR(bar,blah)andfoo = NOT(bar)wherefoo,barandblahare variable names. (We call this a straight-line program since it contains no loops or branching (e.g., if/then) statements.)
To make the second definition more precise, we will now define a programming language that is equivalent to Boolean circuits. We call this programming language the AON-CIRC programming language (“AON” stands for AND/OR/NOT; “CIRC” stands for circuit).
For example, the following is an AON-CIRC program that on input \(x \in \{0,1\}^2\), outputs \(\overline{x_0 \wedge x_1}\) (i.e., the \(\ensuremath{\mathit{NOT}}\) operation applied to \(\ensuremath{\mathit{AND}}(x_0,x_1)\):
AON-CIRC is not a practical programming language: it was designed for pedagogical purposes only, as a way to model computation as the composition of \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\). However, it can still be easily implemented on a computer.
Given this example, you might already be able to guess how to write a program for computing (for example) \(x_0 \wedge \overline{x_1 \vee x_2}\), and in general how to translate a Boolean circuit into an AON-CIRC program. However, since we will want to prove mathematical statements about AON-CIRC programs, we will need to precisely define the AON-CIRC programming language. Precise specifications of programming languages can sometimes be long and tedious,2 but are crucial for secure and reliable implementations. Luckily, the AON-CIRC programming language is simple enough that we can define it formally with relatively little pain.
Specification of the AON-CIRC programming language
An AON-CIRC program is a sequence of strings, which we call “lines”, satisfying the following conditions:
Every line has one of the following forms:
foo = AND(bar,baz),foo = OR(bar,baz), orfoo = NOT(bar)wherefoo,barandbazare variable identifiers. (We follow the common programming languages convention of using names such asfoo,bar,bazas stand-ins for generic identifiers.) The linefoo = AND(bar,baz)corresponds to the operation of assigning to the variablefoothe logical AND of the values of the variablesbarandbaz. Similarlyfoo = OR(bar,baz)andfoo = NOT(bar)correspond to the logical OR and logical NOT operations.A variable identifier in the AON-CIRC programming language can be any combination of letters, numbers, underscores, and brackets. There are two special types of variables:
- Variables of the form
X[\(i\)], with \(i \in \{0,1,\ldots, n-1\}\) are known as input variables. - Variables of the form
Y[\(j\)]are known as output variables.
- Variables of the form
A valid AON-CIRC program \(P\) includes input variables of the form
X[\(0\)],\(\ldots\),X[\(n-1\)]and output variables of the formY[\(0\)],\(\ldots\),Y[\(m-1\)]where \(n,m\) are natural numbers. We say that \(n\) is the number of inputs of the program \(P\) and \(m\) is the number of outputs.In a valid AON-CIRC program, in every line the variables on the right-hand side of the assignment operator must either be input variables or variables that have already been assigned a value in a previous line.
If \(P\) is a valid AON-CIRC program of \(n\) inputs and \(m\) outputs, then for every \(x\in \{0,1\}^n\) the output of \(P\) on input \(x\) is the string \(y\in \{0,1\}^m\) defined as follows:
- Initialize the input variables
X[\(0\)],\(\ldots\),X[\(n-1\)]to the values \(x_0,\ldots,x_{n-1}\) - Run the operator lines of \(P\) one by one in order, in each line assigning to the variable on the left-hand side of the assignment operators the value of the operation on the right-hand side.
- Let \(y\in \{0,1\}^m\) be the values of the output variables
Y[\(0\)],\(\ldots\),Y[\(m-1\)]at the end of the execution.
- Initialize the input variables
We denote the output of \(P\) on input \(x\) by \(P(x)\).
The size of an AON circ program \(P\) is the number of lines it contains. (The reader might note that this corresponds to our definition of the size of a circuit as the number of gates it contains.)
Now that we formally specified AON-CIRC programs, we can define what it means for an AON-CIRC program \(P\) to compute a function \(f\):
Let \(f:\{0,1\}^n \rightarrow\{0,1\}^m\), and \(P\) be a valid AON-CIRC program with \(n\) inputs and \(m\) outputs. We say that \(P\) computes \(f\) if \(P(x)=f(x)\) for every \(x\in \{0,1\}^n\).
The following solved exercise gives an example of an AON-CIRC program.
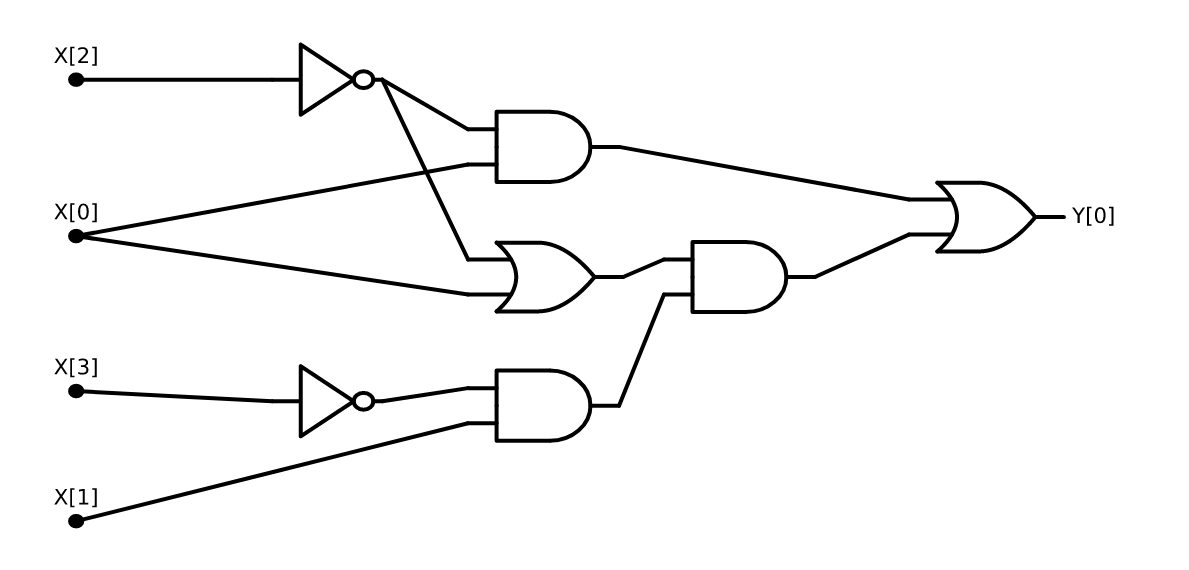
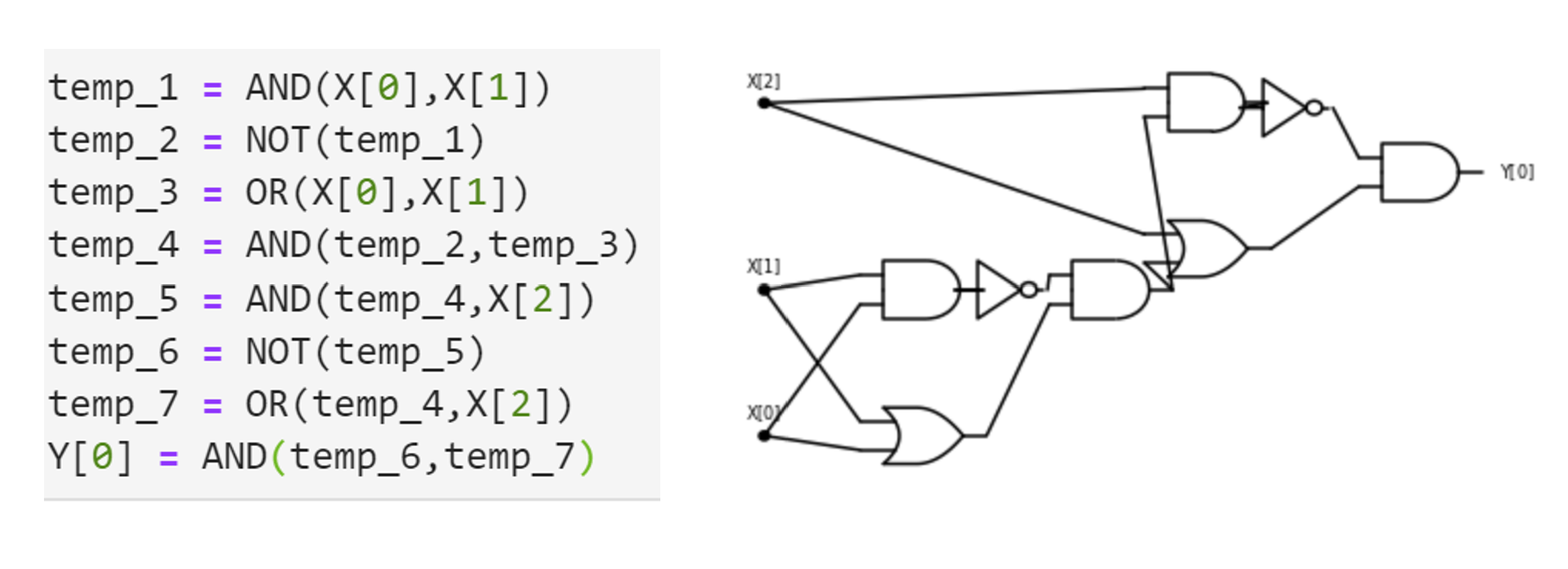
Consider the following function \(\ensuremath{\mathit{CMP}}:\{0,1\}^4 \rightarrow \{0,1\}\) that on four input bits \(a,b,c,d\in \{0,1\}\), outputs \(1\) iff the number represented by \((a,b)\) is larger than the number represented by \((c,d)\). That is \(\ensuremath{\mathit{CMP}}(a,b,c,d)=1\) iff \(2a+b>2c+d\).
Write an AON-CIRC program to compute \(\ensuremath{\mathit{CMP}}\).
Writing such a program is tedious but not truly hard. To compare two numbers we first compare their most significant digit, and then go down to the next digit and so on and so forth. In this case where the numbers have just two binary digits, these comparisons are particularly simple. The number represented by \((a,b)\) is larger than the number represented by \((c,d)\) if and only if one of the following conditions happens:
- The most significant bit \(a\) of \((a,b)\) is larger than the most significant bit \(c\) of \((c,d)\).
or
- The two most significant bits \(a\) and \(c\) are equal, but \(b>d\).
Another way to express the same condition is the following: the number \((a,b)\) is larger than \((c,d)\) iff \(a>c\) OR (\(a\ge c\) AND \(b>d\)).
For binary digits \(\alpha,\beta\), the condition \(\alpha>\beta\) is simply that \(\alpha=1\) and \(\beta=0\) or \(\ensuremath{\mathit{AND}}(\alpha,\ensuremath{\mathit{NOT}}(\beta))=1\), and the condition \(\alpha\ge\beta\) is simply \(\ensuremath{\mathit{OR}}(\alpha, \ensuremath{\mathit{NOT}}(\beta))=1\). Together these observations can be used to give the following AON-CIRC program to compute \(\ensuremath{\mathit{CMP}}\):
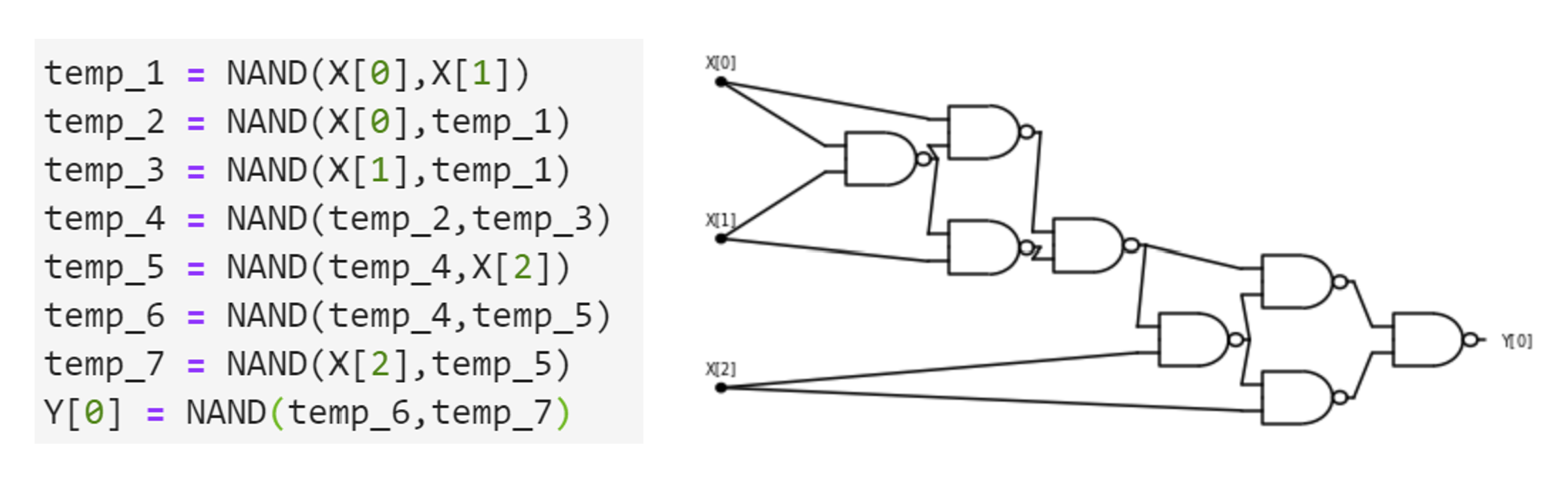
# Compute CMP:{0,1}^4-->{0,1}
# CMP(X)=1 iff 2X[0]+X[1] > 2X[2] + X[3]
temp_1 = NOT(X[2])
temp_2 = AND(X[0],temp_1)
temp_3 = OR(X[0],temp_1)
temp_4 = NOT(X[3])
temp_5 = AND(X[1],temp_4)
temp_6 = AND(temp_5,temp_3)
Y[0] = OR(temp_2,temp_6)We can also present this 8-line program as a circuit with 8 gates, see Figure 3.12.
Proving equivalence of AON-CIRC programs and Boolean circuits
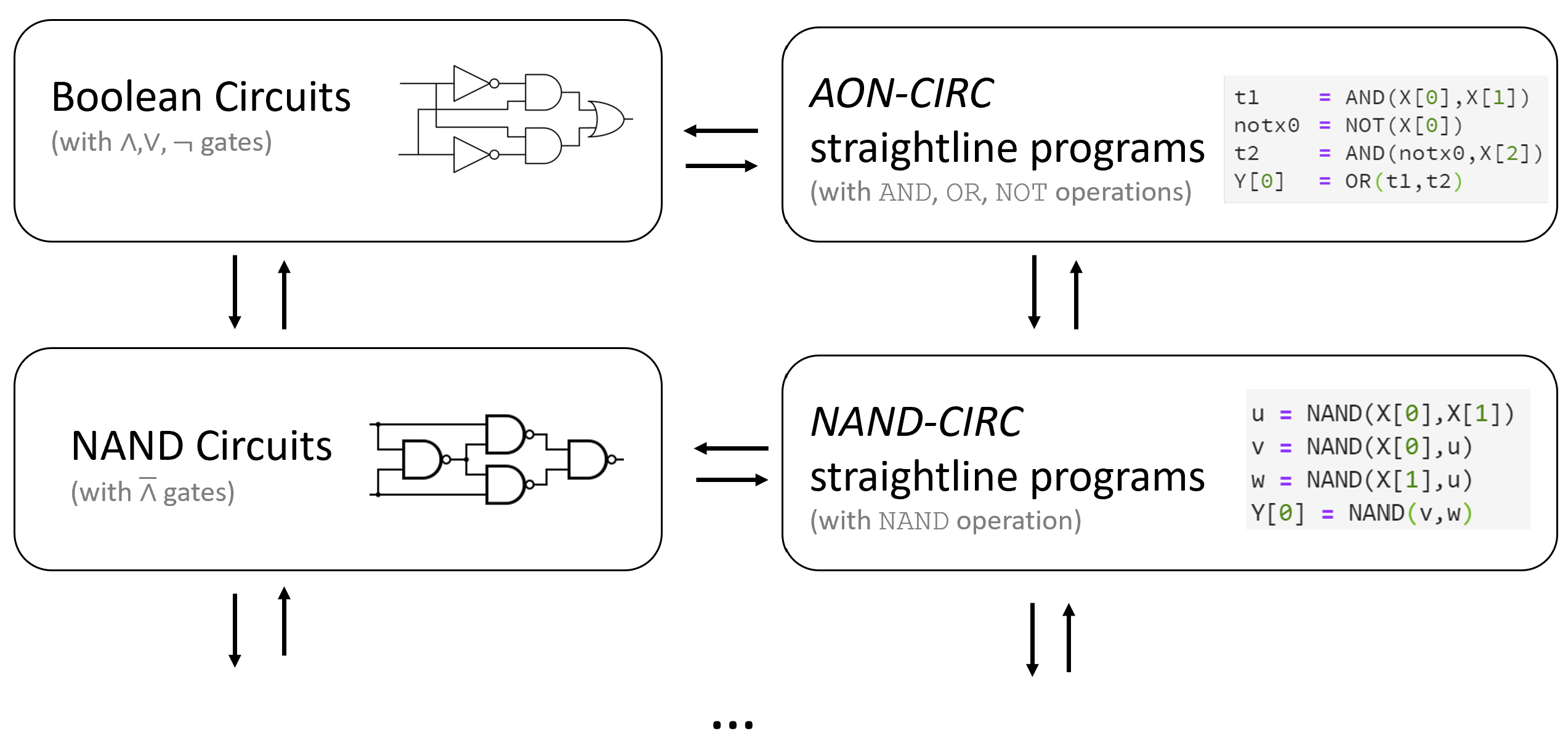
We now formally prove that AON-CIRC programs and Boolean circuits have exactly the same power:
Let \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) and \(s \geq m\) be some number. Then \(f\) is computable by a Boolean circuit with \(s\) gates if and only if \(f\) is computable by an AON-CIRC program of \(s\) lines.
The idea is simple - AON-CIRC programs and Boolean circuits are just different ways of describing the exact same computational process. For example, an AND gate in a Boolean circuit corresponds to computing the AND of two previously-computed values. In an AON-CIRC program this will correspond to the line that stores in a variable the AND of two previously-computed variables.
This proof of Theorem 3.9 is simple at heart, but all the details it contains can make it a little cumbersome to read. You might be better off trying to work it out yourself before reading it. Our GitHub repository contains a “proof by Python” of Theorem 3.9: implementation of functions circuit2prog and prog2circuits mapping Boolean circuits to AON-CIRC programs and vice versa.
Let \(f:\{0,1\}^n \rightarrow \{0,1\}^m\). Since the theorem is an “if and only if” statement, to prove it we need to show both directions: translating an AON-CIRC program that computes \(f\) into a circuit that computes \(f\), and translating a circuit that computes \(f\) into an AON-CIRC program that does so.
We start with the first direction. Let \(P\) be an AON-CIRC program that computes \(f\). We define a circuit \(C\) as follows: the circuit will have \(n\) inputs and \(s\) gates. For every \(i \in [s]\), if the \(i\)-th operator line has the form foo = AND(bar,blah) then the \(i\)-th gate in the circuit will be an AND gate that is connected to gates \(j\) and \(k\) where \(j\) and \(k\) correspond to the last lines before \(i\) where the variables bar and blah (respectively) were written to. (For example, if \(i=57\) and the last line bar was written to is \(35\) and the last line blah was written to is \(17\) then the two in-neighbors of gate \(57\) will be gates \(35\) and \(17\).) If either bar or blah is an input variable then we connect the gate to the corresponding input vertex instead. If foo is an output variable of the form Y[\(j\)] then we add the same label to the corresponding gate to mark it as an output gate. We do the analogous operations if the \(i\)-th line involves an OR or a NOT operation (except that we use the corresponding OR or NOT gate, and in the latter case have only one in-neighbor instead of two). For every input \(x\in \{0,1\}^n\), if we run the program \(P\) on \(x\), then the value written that is computed in the \(i\)-th line is exactly the value that will be assigned to the \(i\)-th gate if we evaluate the circuit \(C\) on \(x\). Hence \(C(x)=P(x)\) for every \(x\in \{0,1\}^n\).
For the other direction, let \(C\) be a circuit of \(s\) gates and \(n\) inputs that computes the function \(f\). We sort the gates according to a topological order and write them as \(v_0,\ldots,v_{s-1}\). We now can create a program \(P\) of \(s\) operator lines as follows. For every \(i\in [s]\), if \(v_i\) is an AND gate with in-neighbors \(v_j,v_k\) then we will add a line to \(P\) of the form temp_\(i\) = AND(temp_\(j\),temp_\(k\)), unless one of the vertices is an input vertex or an output gate, in which case we change this to the form X[.] or Y[.] appropriately. Because we work in topological ordering, we are guaranteed that the in-neighbors \(v_j\) and \(v_k\) correspond to variables that have already been assigned a value. We do the same for OR and NOT gates. Once again, one can verify that for every input \(x\), the value \(P(x)\) will equal \(C(x)\) and hence the program computes the same function as the circuit. (Note that since \(C\) is a valid circuit, per Definition 3.5, every input vertex of \(C\) has at least one out-neighbor and there are exactly \(m\) output gates labeled \(0,\ldots,m-1\); hence all the variables X[0], \(\ldots\), X[\(n-1\)] and Y[0] ,\(\ldots\), Y[\(m-1\)] will appear in the program \(P\).)
Physical implementations of computing devices (digression)
Computation is an abstract notion that is distinct from its physical implementations. While most modern computing devices are obtained by mapping logical gates to semiconductor-based transistors, throughout history people have computed using a huge variety of mechanisms, including mechanical systems, gas and liquid (known as fluidics), biological and chemical processes, and even living creatures (e.g., see Figure 3.14 or this video for how crabs or slime mold can be used to do computations).
In this section we will review some of these implementations, both so you can get an appreciation of how it is possible to directly translate Boolean circuits to the physical world, without going through the entire stack of architecture, operating systems, and compilers, as well as to emphasize that silicon-based processors are by no means the only way to perform computation. Indeed, as we will see in Chapter 23, a very exciting recent line of work involves using different media for computation that would allow us to take advantage of quantum mechanical effects to enable different types of algorithms.
Such a cool way to explain logic gates. pic.twitter.com/6Wgu2ZKFCx
— Lionel Page (@page_eco) October 28, 2019
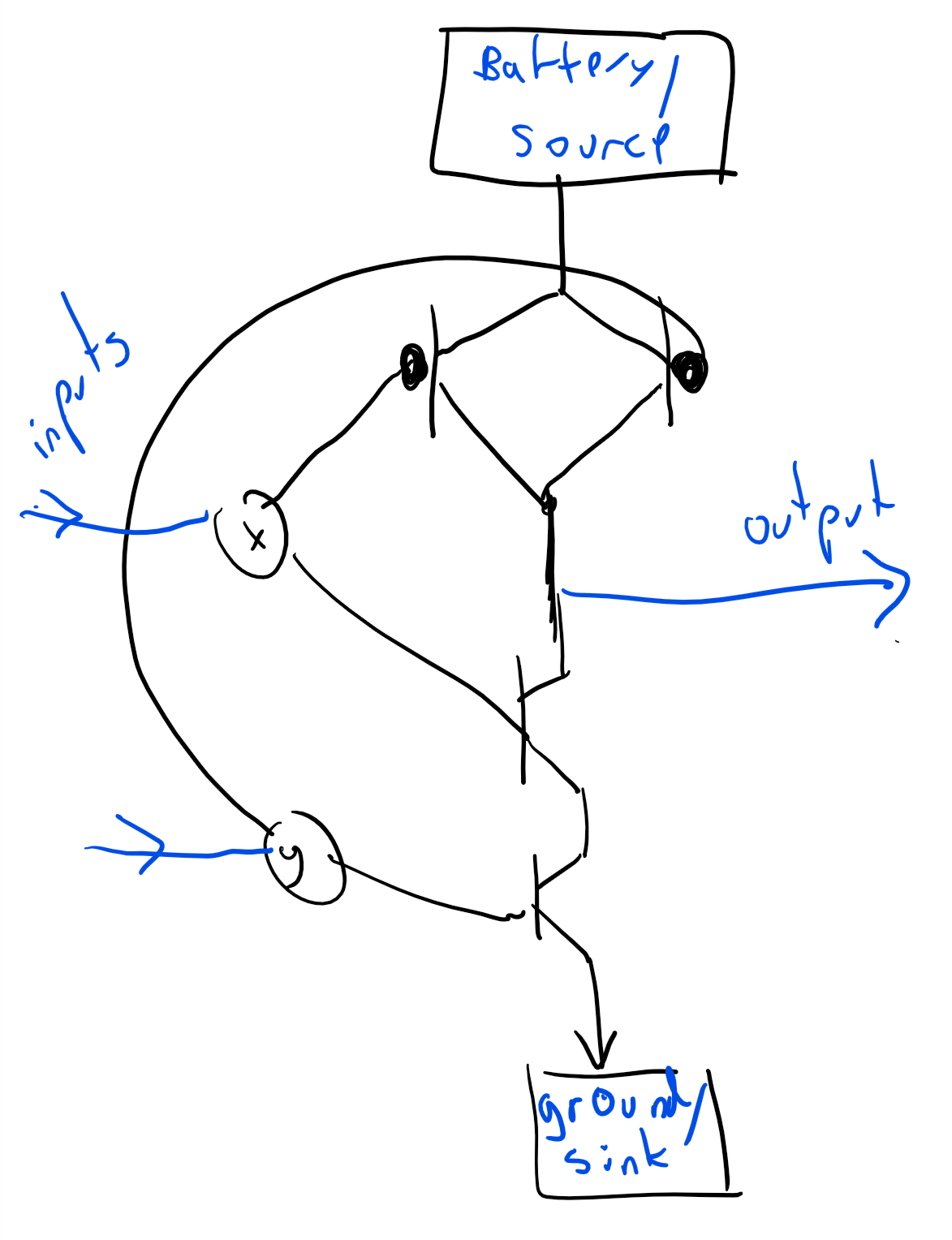
Transistors
A transistor can be thought of as an electric circuit with two inputs, known as the source and the gate and an output, known as the sink. The gate controls whether current flows from the source to the sink. In a standard transistor, if the gate is “ON” then current can flow from the source to the sink and if it is “OFF” then it can’t. In a complementary transistor this is reversed: if the gate is “OFF” then current can flow from the source to the sink and if it is “ON” then it can’t.
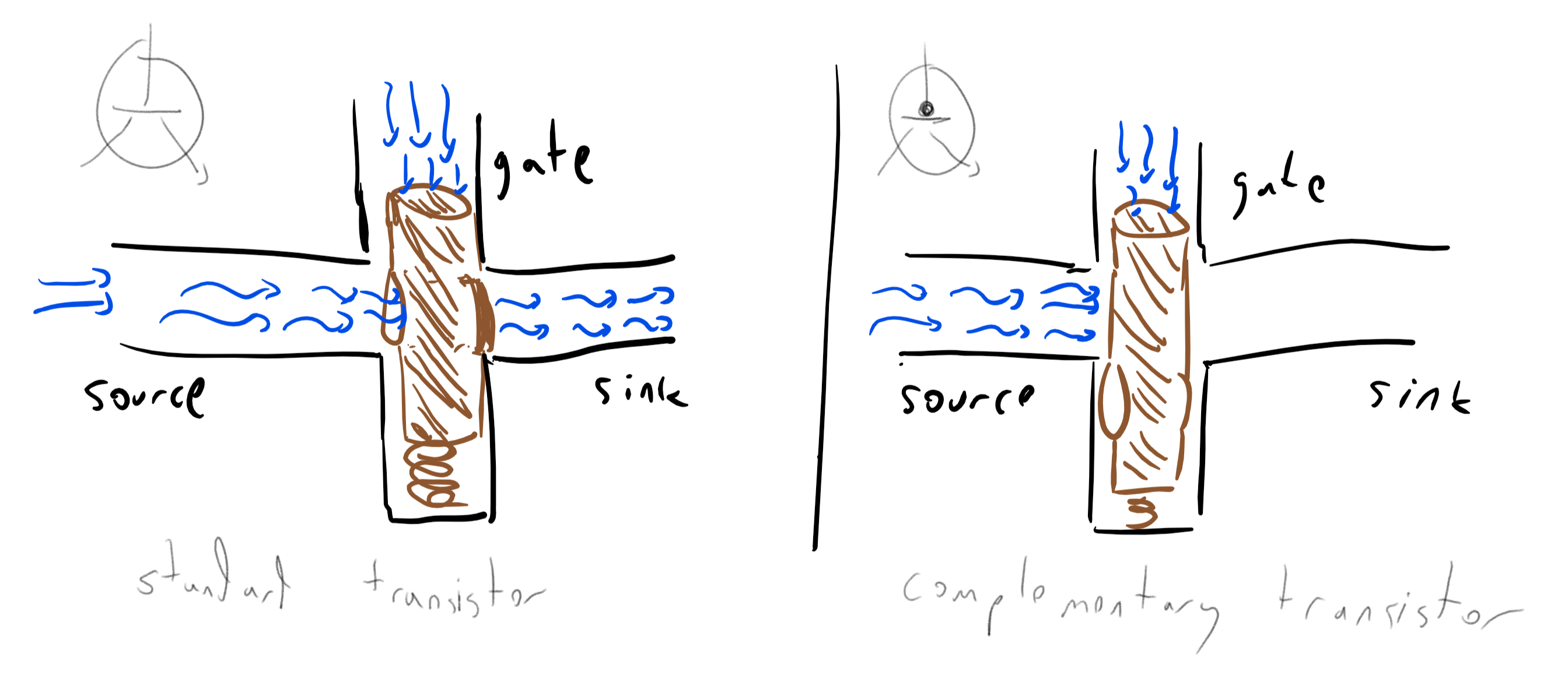
There are several ways to implement the logic of a transistor. For example, we can use faucets to implement it using water pressure (e.g. Figure 3.15). This might seem as merely a curiosity, but there is a field known as fluidics concerned with implementing logical operations using liquids or gasses. Some of the motivations include operating in extreme environmental conditions such as in space or a battlefield, where standard electronic equipment would not survive.
The standard implementations of transistors use electrical current. One of the original implementations used vacuum tubes. As its name implies, a vacuum tube is a tube containing nothing (i.e., a vacuum) and where a priori electrons could freely flow from the source (a wire) to the sink (a plate). However, there is a gate (a grid) between the two, where modulating its voltage can block the flow of electrons.
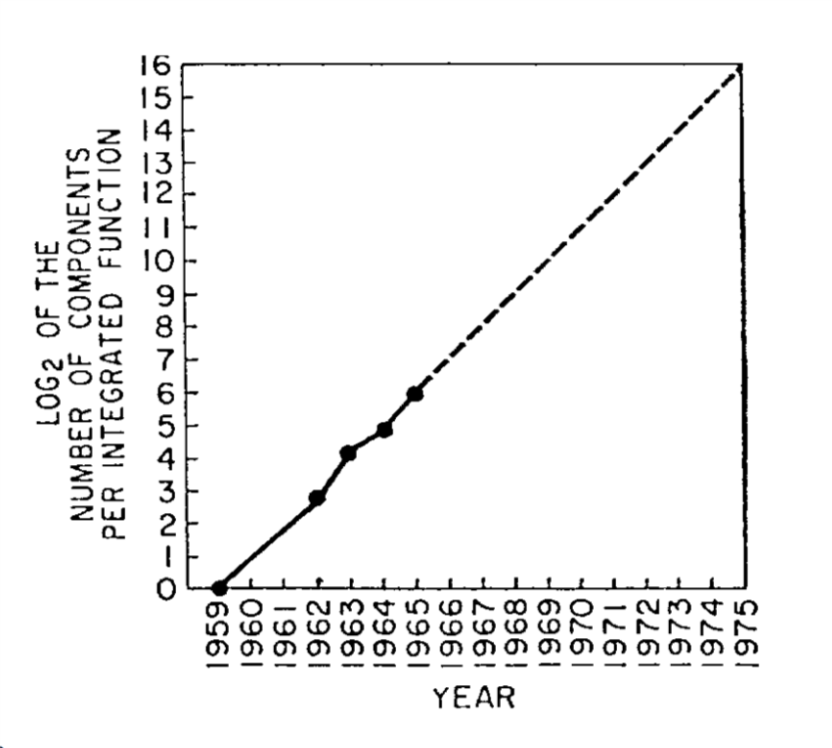
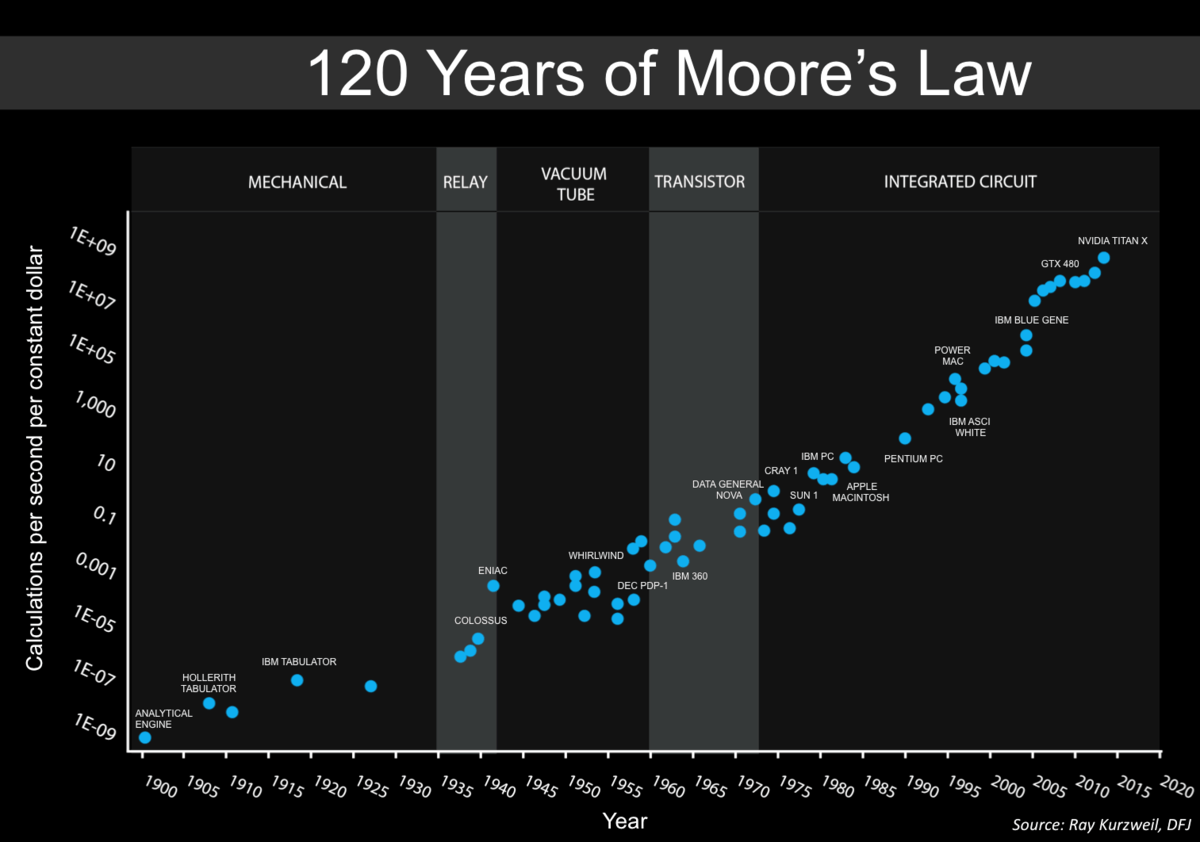
Early vacuum tubes were roughly the size of lightbulbs (and looked very much like them too). In the 1950’s they were supplanted by transistors, which implement the same logic using semiconductors which are materials that normally do not conduct electricity but whose conductivity can be modified and controlled by inserting impurities (“doping”) and applying an external electric field (this is known as the field effect). In the 1960’s computers started to be implemented using integrated circuits which enabled much greater density. In 1965, Gordon Moore predicted that the number of transistors per integrated circuit would double every year (see Figure 3.16), and that this would lead to “such wonders as home computers —or at least terminals connected to a central computer— automatic controls for automobiles, and personal portable communications equipment”. Since then, (adjusted versions of) this so-called “Moore’s law” have been running strong, though exponential growth cannot be sustained forever, and some physical limitations are already becoming apparent.

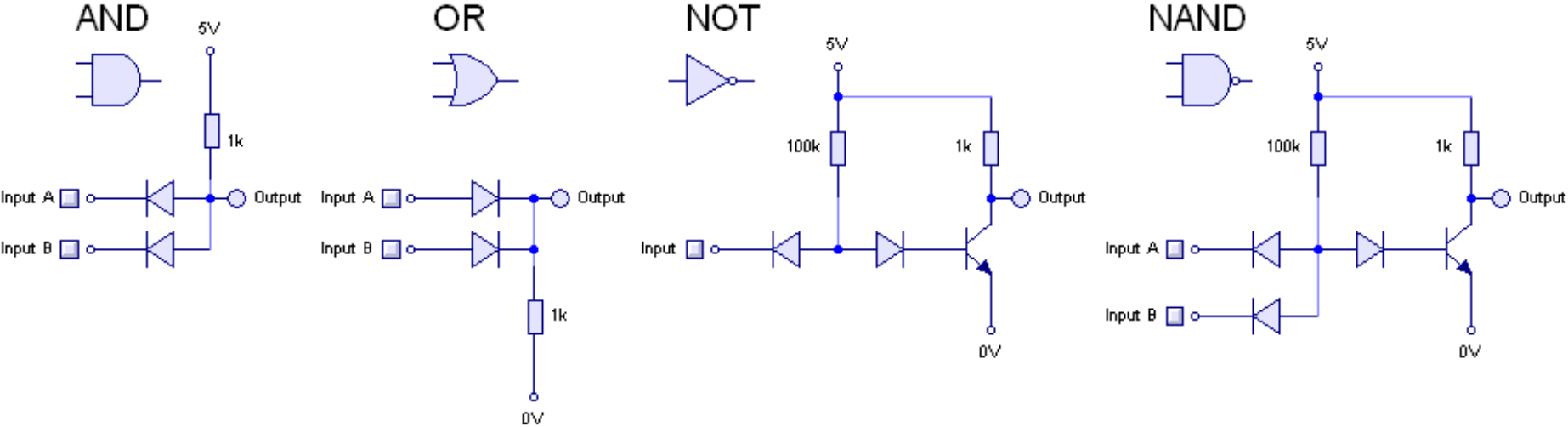
Logical gates from transistors
We can use transistors to implement various Boolean functions such as \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\). For each two-input gate \(G:\{0,1\}^2 \rightarrow \{0,1\}\), such an implementation would be a system with two input wires \(x,y\) and one output wire \(z\), such that if we identify high voltage with “\(1\)” and low voltage with “\(0\)”, then the wire \(z\) will be equal to “\(1\)” if and only if applying \(G\) to the values of the wires \(x\) and \(y\) is \(1\) (see Figure 3.19 and Figure 3.20). This means that if there exists a AND/OR/NOT circuit to compute a function \(g:\{0,1\}^n \rightarrow \{0,1\}^m\), then we can compute \(g\) in the physical world using transistors as well.
Biological computing
Computation can be based on biological or chemical systems. For example the lac operon produces the enzymes needed to digest lactose only if the conditions \(x \wedge (\neg y)\) hold where \(x\) is “lactose is present” and \(y\) is “glucose is present”. Researchers have managed to create transistors, and from them logic gates, based on DNA molecules (see also Figure 3.21). Projects such as the Cello programming language enable converting Boolean circuits into DNA sequences that encode operations that can be executed in bacterial cells, see this video. One motivation for DNA computing is to achieve increased parallelism or storage density; another is to create “smart biological agents” that could perhaps be injected into bodies, replicate themselves, and fix or kill cells that were damaged by a disease such as cancer. Computing in biological systems is not restricted, of course, to DNA: even larger systems such as flocks of birds can be considered as computational processes.
Cellular automata and the game of life
Cellular automata is a model of a system composed of a sequence of cells, each of which can have a finite state. At each step, a cell updates its state based on the states of its neighboring cells and some simple rules. As we will discuss later in this book (see Section 8.4), cellular automata such as Conway’s “Game of Life” can be used to simulate computation gates.
Neural networks
One computation device that we all carry with us is our own brain. Brains have served humanity throughout history, doing computations that range from distinguishing prey from predators, through making scientific discoveries and artistic masterpieces, to composing witty 280 character messages. The exact working of the brain is still not fully understood, but one common mathematical model for it is a (very large) neural network.
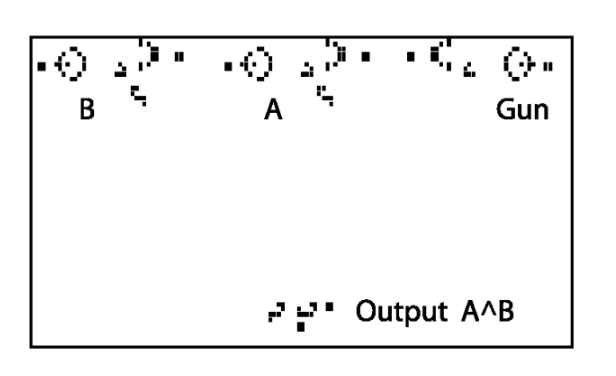
A neural network can be thought of as a Boolean circuit that instead of \(\ensuremath{\mathit{AND}}\)/\(\ensuremath{\mathit{OR}}\)/\(\ensuremath{\mathit{NOT}}\) uses some other gates as the basic basis. For example, one particular basis we can use are threshold gates. For every vector \(w= (w_0,\ldots,w_{k-1})\) of integers and integer \(t\) (some or all of which could be negative), the threshold function corresponding to \(w,t\) is the function \(T_{w,t}:\{0,1\}^k \rightarrow \{0,1\}\) that maps \(x\in \{0,1\}^k\) to \(1\) if and only if \(\sum_{i=0}^{k-1} w_i x_i \geq t\). For example, the threshold function \(T_{w,t}\) corresponding to \(w=(1,1,1,1,1)\) and \(t=3\) is simply the majority function \(\ensuremath{\mathit{MAJ}}_5\) on \(\{0,1\}^5\). Threshold gates can be thought of as an approximation for neuron cells that make up the core of human and animal brains. To a first approximation, a neuron has \(k\) inputs and a single output, and the neuron “fires” or “turns on” its output when those signals pass some threshold.
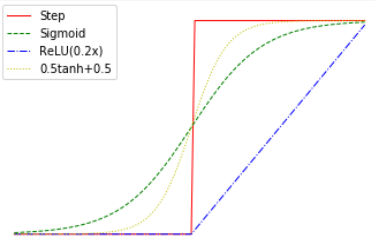
Many machine learning algorithms use artificial neural networks whose purpose is not to imitate biology but rather to perform some computational tasks, and hence are not restricted to a threshold or other biologically-inspired gates. Generally, a neural network is often described as operating on signals that are real numbers, rather than \(0/1\) values, and where the output of a gate on inputs \(x_0,\ldots,x_{k-1}\) is obtained by applying \(f(\sum_i w_i x_i)\) where \(f:\R \rightarrow \R\) is an activation function such as rectified linear unit (ReLU), Sigmoid, or many others (see Figure 3.23). However, for the purposes of our discussion, all of the above are equivalent (see also Exercise 3.13). In particular we can reduce the setting of real inputs to binary inputs by representing a real number in the binary basis, and multiplying the weight of the bit corresponding to the \(i^{th}\) digit by \(2^i\).
A computer made from marbles and pipes
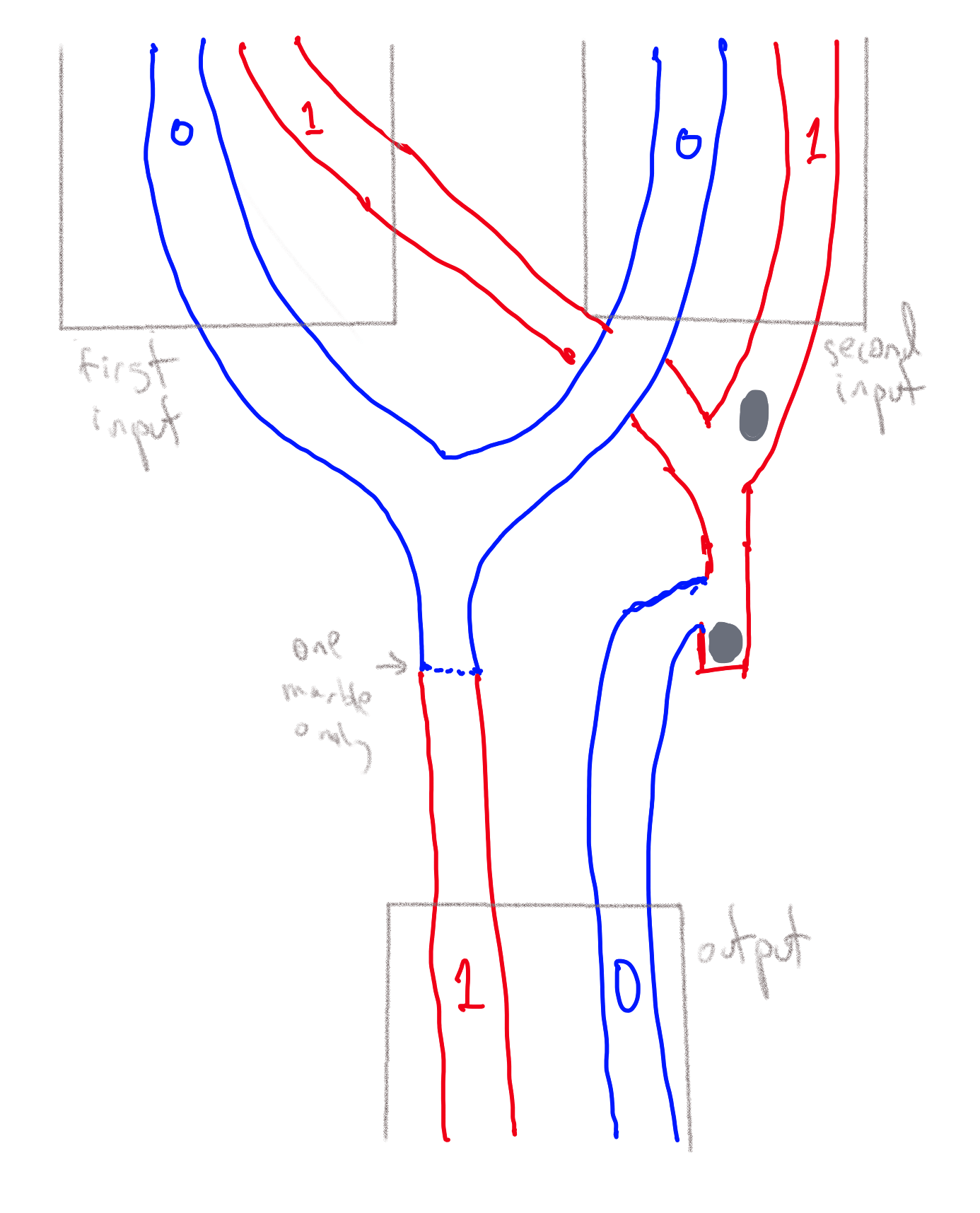
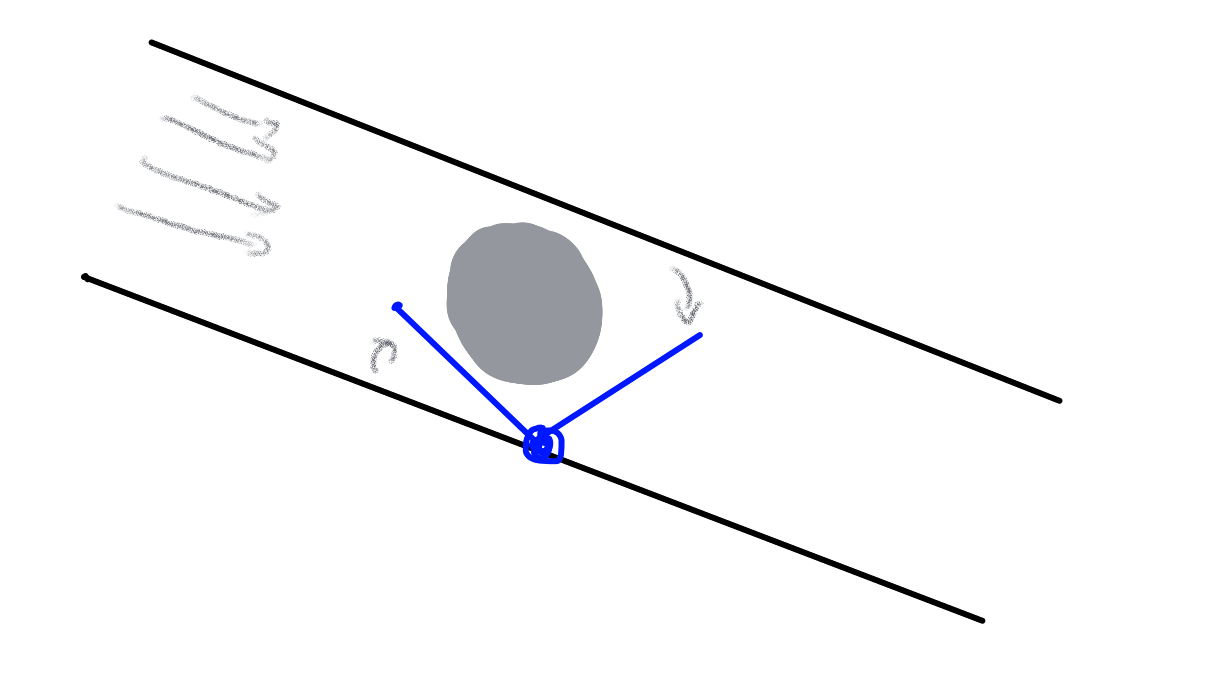
We can implement computation using many other physical media, without any electronic, biological, or chemical components. Many suggestions for mechanical computers have been put forward, going back at least to Gottfried Leibniz’s computing machines from the 1670s and Charles Babbage’s 1837 plan for a mechanical “Analytical Engine”. As one example, Figure 3.24 shows a simple implementation of a NAND (negation of AND, see Section 3.6) gate using marbles going through pipes. We represent a logical value in \(\{0,1\}\) by a pair of pipes, such that there is a marble flowing through exactly one of the pipes. We call one of the pipes the “\(0\) pipe” and the other the “\(1\) pipe”, and so the identity of the pipe containing the marble determines the logical value. A NAND gate corresponds to a mechanical object with two pairs of incoming pipes and one pair of outgoing pipes, such that for every \(a,b \in \{0,1\}\), if two marbles are rolling toward the object in the \(a\) pipe of the first pair and the \(b\) pipe of the second pair, then a marble will roll out of the object in the \(\ensuremath{\mathit{NAND}}(a,b)\)-pipe of the outgoing pair. In fact, there is even a commercially-available educational game that uses marbles as a basis of computing, see Figure 3.26.

The NAND function
The \(\ensuremath{\mathit{NAND}}\) function is another simple function that is extremely useful for defining computation. It is the function mapping \(\{0,1\}^2\) to \(\{0,1\}\) defined by:
As its name implies, \(\ensuremath{\mathit{NAND}}\) is the NOT of AND (i.e., \(\ensuremath{\mathit{NAND}}(a,b)= \ensuremath{\mathit{NOT}}(\ensuremath{\mathit{AND}}(a,b))\)), and so we can clearly compute \(\ensuremath{\mathit{NAND}}\) using \(\ensuremath{\mathit{AND}}\) and \(\ensuremath{\mathit{NOT}}\). Interestingly, the opposite direction holds as well:
We can compute \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\) by composing only the \(\ensuremath{\mathit{NAND}}\) function.
We start with the following observation. For every \(a\in \{0,1\}\), \(\ensuremath{\mathit{AND}}(a,a)=a\). Hence, \(\ensuremath{\mathit{NAND}}(a,a)=\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{AND}}(a,a))=\ensuremath{\mathit{NOT}}(a)\). This means that \(\ensuremath{\mathit{NAND}}\) can compute \(\ensuremath{\mathit{NOT}}\). By the principle of “double negation”, \(\ensuremath{\mathit{AND}}(a,b)=\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{AND}}(a,b)))\), and hence we can use \(\ensuremath{\mathit{NAND}}\) to compute \(\ensuremath{\mathit{AND}}\) as well. Once we can compute \(\ensuremath{\mathit{AND}}\) and \(\ensuremath{\mathit{NOT}}\), we can compute \(\ensuremath{\mathit{OR}}\) using “De Morgan’s Law”: \(\ensuremath{\mathit{OR}}(a,b)=\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{AND}}(\ensuremath{\mathit{NOT}}(a),\ensuremath{\mathit{NOT}}(b)))\) (which can also be written as \(a \vee b = \overline{\overline{a} \wedge \overline{b}}\)) for every \(a,b \in \{0,1\}\).
Theorem 3.10’s proof is very simple, but you should make sure that (i) you understand the statement of the theorem, and (ii) you follow its proof. In particular, you should make sure you understand why De Morgan’s law is true.
We can use \(\ensuremath{\mathit{NAND}}\) to compute many other functions, as demonstrated in the following exercise.
Let \(\ensuremath{\mathit{MAJ}}: \{0,1\}^3 \rightarrow \{0,1\}\) be the function that on input \(a,b,c\) outputs \(1\) iff \(a+b+c \geq 2\). Show how to compute \(\ensuremath{\mathit{MAJ}}\) using a composition of \(\ensuremath{\mathit{NAND}}\)’s.
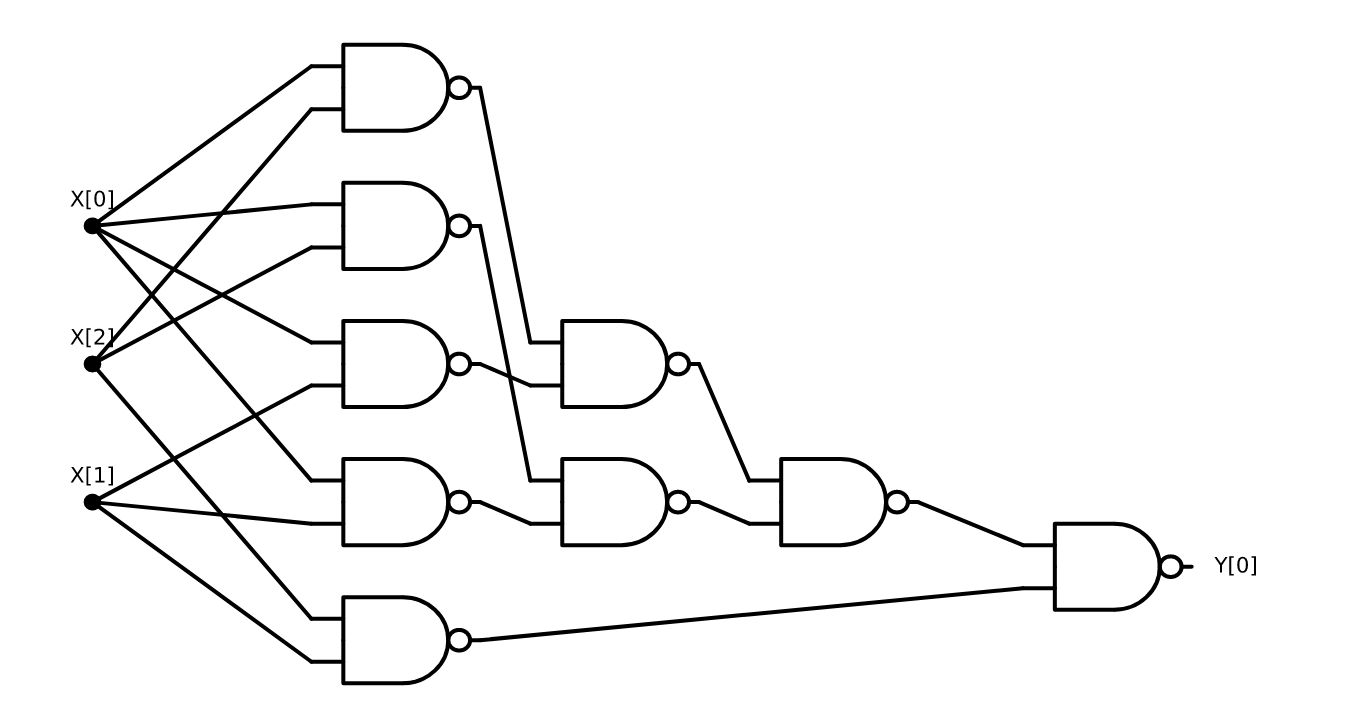
Recall that Equation 3.1 states that
We can use Theorem 3.10 to replace all the occurrences of \(\ensuremath{\mathit{AND}}\) and \(\ensuremath{\mathit{OR}}\) with \(\ensuremath{\mathit{NAND}}\)’s. Specifically, we can use the equivalence \(\ensuremath{\mathit{AND}}(a,b)=\ensuremath{\mathit{NOT}}(\ensuremath{\mathit{NAND}}(a,b))\), \(\ensuremath{\mathit{OR}}(a,b)=\ensuremath{\mathit{NAND}}(\ensuremath{\mathit{NOT}}(a),\ensuremath{\mathit{NOT}}(b))\), and \(\ensuremath{\mathit{NOT}}(a)=\ensuremath{\mathit{NAND}}(a,a)\) to replace the right-hand side of Equation 3.2 with an expression involving only \(\ensuremath{\mathit{NAND}}\), yielding that \(\ensuremath{\mathit{MAJ}}(a,b,c)\) is equivalent to the (somewhat unwieldy) expression
The same formula can also be expressed as a circuit with NAND gates, see Figure 3.27.
NAND Circuits
We define NAND Circuits as circuits in which all the gates are NAND operations. Such a circuit again corresponds to a directed acyclic graph (DAG) since all the gates correspond to the same function (i.e., NAND), we do not even need to label them, and all gates have in-degree exactly two. Despite their simplicity, NAND circuits can be quite powerful.
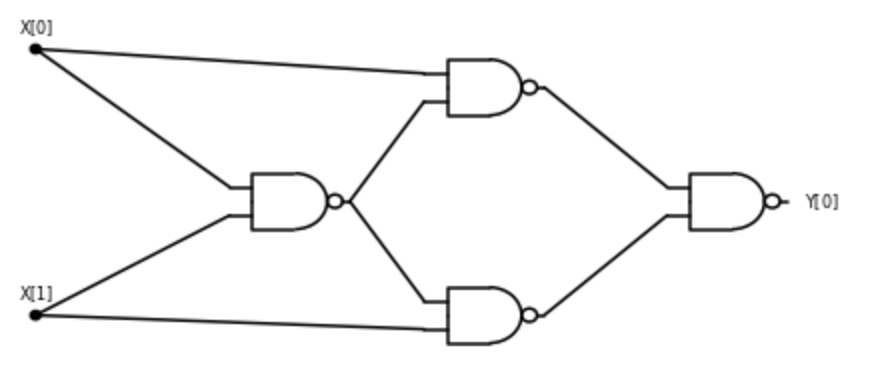
Recall the \(\ensuremath{\mathit{XOR}}\) function which maps \(x_0,x_1 \in \{0,1\}\) to \(x_0 + x_1 \mod 2\). We have seen in Section 3.2.2 that we can compute \(\ensuremath{\mathit{XOR}}\) using \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\), and \(\ensuremath{\mathit{NOT}}\), and so by Theorem 3.10 we can compute it using only \(\ensuremath{\mathit{NAND}}\)’s. However, the following is a direct construction of computing \(\ensuremath{\mathit{XOR}}\) by a sequence of NAND operations:
- Let \(u = \ensuremath{\mathit{NAND}}(x_0,x_1)\).
- Let \(v = \ensuremath{\mathit{NAND}}(x_0,u)\)
- Let \(w = \ensuremath{\mathit{NAND}}(x_1,u)\).
- The \(\ensuremath{\mathit{XOR}}\) of \(x_0\) and \(x_1\) is \(y_0 = \ensuremath{\mathit{NAND}}(v,w)\).
One can verify that this algorithm does indeed compute \(\ensuremath{\mathit{XOR}}\) by enumerating all the four choices for \(x_0,x_1 \in \{0,1\}\). We can also represent this algorithm graphically as a circuit, see Figure 3.28.
In fact, we can show the following theorem:
For every Boolean circuit \(C\) of \(s\) gates, there exists a NAND circuit \(C'\) of at most \(3s\) gates that computes the same function as \(C\).
The idea of the proof is to just replace every \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) and \(\ensuremath{\mathit{NOT}}\) gate with their NAND implementation following the proof of Theorem 3.10.
If \(C\) is a Boolean circuit, then since, as we’ve seen in the proof of Theorem 3.10, for every \(a,b \in \{0,1\}\)
\(\ensuremath{\mathit{NOT}}(a) = \ensuremath{\mathit{NAND}}(a,a)\)
\(\ensuremath{\mathit{AND}}(a,b) = \ensuremath{\mathit{NAND}}(\ensuremath{\mathit{NAND}}(a,b),\ensuremath{\mathit{NAND}}(a,b))\)
\(\ensuremath{\mathit{OR}}(a,b) = \ensuremath{\mathit{NAND}}(\ensuremath{\mathit{NAND}}(a,a),\ensuremath{\mathit{NAND}}(b,b))\)
we can replace every gate of \(C\) with at most three \(\ensuremath{\mathit{NAND}}\) gates to obtain an equivalent circuit \(C'\). The resulting circuit will have at most \(3s\) gates.
Two models are equivalent in power if they can be used to compute the same set of functions.
More examples of NAND circuits (optional)
Here are some more sophisticated examples of NAND circuits:
Incrementing integers. Consider the task of computing, given as input a string \(x\in \{0,1\}^n\) that represents a natural number \(X\in \N\), the representation of \(X+1\). That is, we want to compute the function \(\ensuremath{\mathit{INC}}_n:\{0,1\}^n \rightarrow \{0,1\}^{n+1}\) such that for every \(x_0,\ldots,x_{n-1}\), \(\ensuremath{\mathit{INC}}_n(x)=y\) which satisfies \(\sum_{i=0}^n y_i 2^i = \left( \sum_{i=0}^{n-1} x_i 2^i \right)+1\). (For simplicity of notation, in this example we use the representation where the least significant digit is first rather than last.)
The increment operation can be very informally described as follows: “Add \(1\) to the least significant bit and propagate the carry”. A little more precisely, in the case of the binary representation, to obtain the increment of \(x\), we scan \(x\) from the least significant bit onwards, and flip all \(1\)’s to \(0\)’s until we encounter a bit equal to \(0\), in which case we flip it to \(1\) and stop.
Thus we can compute the increment of \(x_0,\ldots,x_{n-1}\) by doing the following:
Algorithm 3.13 Compute Increment Function
Input: \(x_0,x_1,\ldots,x_{n-1}\) representing the number \(\sum_{i=0}^{n-1} x_i\cdot 2^i\) # we use LSB-first representation
Output: \(y \in \{0,1\}^{n+1}\) such that \(\sum_{i=0}^n y_i \cdot 2^i = \sum_{i=0}^{n-1} x_i\cdot 2^i + 1\)
Let \(c_0 \leftarrow 1\) # we pretend we have a "carry" of \(1\) initially
for{\(i=0,\ldots, n-1\)}
Let \(y_i \leftarrow XOR(x_i,c_i)\).
if{\(c_i=x_i=1\)}
\(c_{i+1}=1\)
else
\(c_{i+1}=0\)
endif
endfor
Let \(y_n \leftarrow c_n\).
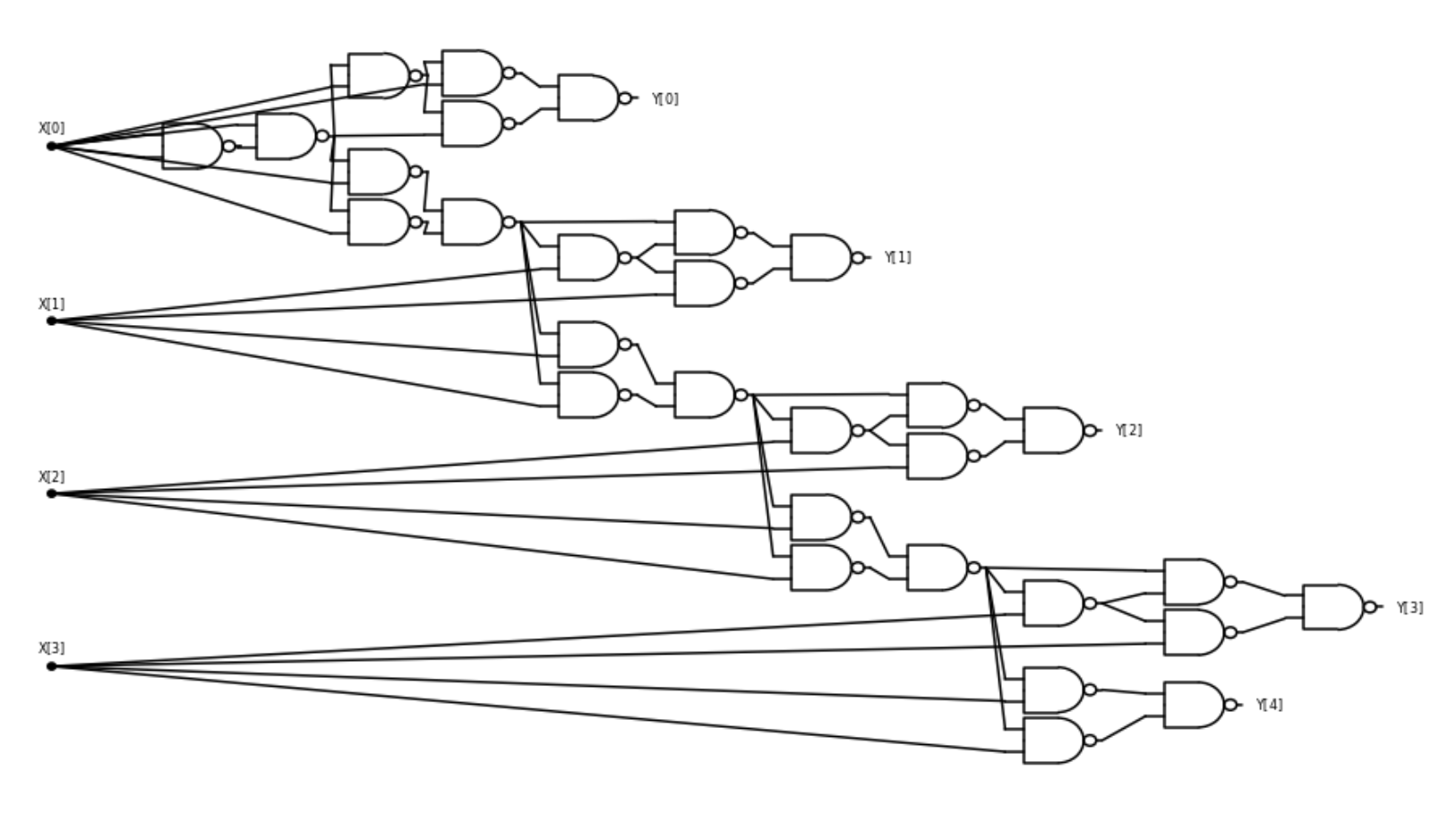
Algorithm 3.13 describes precisely how to compute the increment operation, and can be easily transformed into Python code that performs the same computation, but it does not seem to directly yield a NAND circuit to compute this. However, we can transform this algorithm line by line to a NAND circuit. For example, since for every \(a\), \(\ensuremath{\mathit{NAND}}(a,\ensuremath{\mathit{NOT}}(a))=1\), we can replace the initial statement \(c_0=1\) with \(c_0 = \ensuremath{\mathit{NAND}}(x_0,\ensuremath{\mathit{NAND}}(x_0,x_0))\). We already know how to compute \(\ensuremath{\mathit{XOR}}\) using NAND and so we can use this to implement the operation \(y_i \leftarrow \ensuremath{\mathit{XOR}}(x_i,c_i)\). Similarly, we can write the “if” statement as saying \(c_{i+1} \leftarrow \ensuremath{\mathit{AND}}(c_i,x_i)\), or in other words \(c_{i+1} \leftarrow \ensuremath{\mathit{NAND}}(\ensuremath{\mathit{NAND}}(c_i,x_i),\ensuremath{\mathit{NAND}}(c_i,x_i))\). Finally, the assignment \(y_n = c_n\) can be written as \(y_n = \ensuremath{\mathit{NAND}}(\ensuremath{\mathit{NAND}}(c_n,c_n),\ensuremath{\mathit{NAND}}(c_n,c_n))\). Combining these observations yields for every \(n\in \N\), a \(\ensuremath{\mathit{NAND}}\) circuit to compute \(\ensuremath{\mathit{INC}}_n\). For example, Figure 3.29 shows what this circuit looks like for \(n=4\).
From increment to addition. Once we have the increment operation, we can certainly compute addition by repeatedly incrementing (i.e., compute \(x+y\) by performing \(\ensuremath{\mathit{INC}}(x)\) \(y\) times). However, that would be quite inefficient and unnecessary. With the same idea of keeping track of carries we can implement the “grade-school” addition algorithm and compute the function \(\ensuremath{\mathit{ADD}}_n:\{0,1\}^{2n} \rightarrow \{0,1\}^{n+1}\) that on input \(x\in \{0,1\}^{2n}\) outputs the binary representation of the sum of the numbers represented by \(x_0,\ldots,x_{n-1}\) and \(x_{n},\ldots,x_{2n-1}\):
Algorithm 3.14 Addition using NAND
Input: \(u \in \{0,1\}^n\), \(v\in \{0,1\}^n\) representing numbers in LSB-first binary representation.
Output: LSB-first binary representation of \(x+y\).
Let \(c_0 \leftarrow 0\)
for{\(i=0,\ldots,n-1\)}
Let \(y_i \leftarrow u_i + v_i \mod 2\)
if{\(u_i + v_i + c_i \geq 2\)}
\(c_{i+1}\leftarrow 1\)
else
\(c_{i+1} \leftarrow 0\)
endif
endfor
Let \(y_n \leftarrow c_n\)
Once again, Algorithm 3.14 can be translated into a NAND circuit. The crucial observation is that the “if/then” statement simply corresponds to \(c_{i+1} \leftarrow \ensuremath{\mathit{MAJ}}_3(u_i,v_i,v_i)\) and we have seen in Solved Exercise 3.5 that the function \(\ensuremath{\mathit{MAJ}}_3:\{0,1\}^3 \rightarrow \{0,1\}\) can be computed using \(\ensuremath{\mathit{NAND}}\)s.
The NAND-CIRC Programming language
Just like we did for Boolean circuits, we can define a programming-language analog of NAND circuits. It is even simpler than the AON-CIRC language since we only have a single operation. We define the NAND-CIRC Programming Language to be a programming language where every line (apart from the input/output declaration) has the following form:
where foo, bar and blah are variable identifiers.
Here is an example of a NAND-CIRC program:
Do you know what function this program computes? Hint: you have seen it before.
Formally, just like we did in Definition 3.8 for AON-CIRC, we can define the notion of computation by a NAND-CIRC program in the natural way:
Let \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) be some function, and let \(P\) be a NAND-CIRC program. We say that \(P\) computes the function \(f\) if:
\(P\) has \(n\) input variables
X[\(0\)]\(,\ldots,\)X[\(n-1\)]and \(m\) output variablesY[\(0\)],\(\ldots\),Y[\(m-1\)].For every \(x\in \{0,1\}^n\), if we execute \(P\) when we assign to
X[\(0\)]\(,\ldots,\)X[\(n-1\)]the values \(x_0,\ldots,x_{n-1}\), then at the end of the execution, the output variablesY[\(0\)],\(\ldots\),Y[\(m-1\)]have the values \(y_0,\ldots,y_{m-1}\) where \(y=f(x)\).
As before we can show that NAND circuits are equivalent to NAND-CIRC programs (see Figure 3.30):
For every \(f:\{0,1\}^n \rightarrow \{0,1\}^m\) and \(s \geq m\), \(f\) is computable by a NAND-CIRC program of \(s\) lines if and only if \(f\) is computable by a NAND circuit of \(s\) gates.
We omit the proof of Theorem 3.17 since it follows along exactly the same lines as the equivalence of Boolean circuits and AON-CIRC program (Theorem 3.9). Given Theorem 3.17 and Theorem 3.12, we know that we can translate every \(s\)-line AON-CIRC program \(P\) into an equivalent NAND-CIRC program of at most \(3s\) lines. In fact, this translation can be easily done by replacing every line of the form foo = AND(bar,blah), foo = OR(bar,blah) or foo = NOT(bar) with the equivalent 1-3 lines that use the NAND operation. Our GitHub repository contains a “proof by code”: a simple Python program AON2NAND that transforms an AON-CIRC into an equivalent NAND-CIRC program.
You might have heard of a term called “Turing Complete” that is sometimes used to describe programming languages. (If you haven’t, feel free to ignore the rest of this remark: we define this term precisely in Chapter 8.) If so, you might wonder if the NAND-CIRC programming language has this property. The answer is no, or perhaps more accurately, the term “Turing Completeness” is not really applicable for the NAND-CIRC programming language. The reason is that, by design, the NAND-CIRC programming language can only compute finite functions \(F:\{0,1\}^n \rightarrow \{0,1\}^m\) that take a fixed number of input bits and produce a fixed number of outputs bits. The term “Turing Complete” is only applicable to programming languages for infinite functions that can take inputs of arbitrary length. We will come back to this distinction later on in this book.
Equivalence of all these models
If we put together Theorem 3.9, Theorem 3.12, and Theorem 3.17, we obtain the following result:
For every sufficiently large \(s,n,m\) and \(f:\{0,1\}^n \rightarrow \{0,1\}^m\), the following conditions are all equivalent to one another:
\(f\) can be computed by a Boolean circuit (with \(\wedge,\vee,\neg\) gates) of at most \(O(s)\) gates.
\(f\) can be computed by an AON-CIRC straight-line program of at most \(O(s)\) lines.
\(f\) can be computed by a NAND circuit of at most \(O(s)\) gates.
\(f\) can be computed by a NAND-CIRC straight-line program of at most \(O(s)\) lines.
By “\(O(s)\)” we mean that the bound is at most \(c\cdot s\) where \(c\) is a constant that is independent of \(n\). For example, if \(f\) can be computed by a Boolean circuit of \(s\) gates, then it can be computed by a NAND-CIRC program of at most \(3s\) lines, and if \(f\) can be computed by a NAND circuit of \(s\) gates, then it can be computed by an AON-CIRC program of at most \(2s\) lines.
We omit the formal proof, which is obtained by combining Theorem 3.9, Theorem 3.12, and Theorem 3.17. The key observation is that the results we have seen allow us to translate a program/circuit that computes \(f\) in one of the above models into a program/circuit that computes \(f\) in another model by increasing the lines/gates by at most a constant factor (in fact this constant factor is at most \(3\)).
Theorem 3.9 is a special case of a more general result. We can consider even more general models of computation, where instead of AND/OR/NOT or NAND, we use other operations (see Section 3.7.1 below). It turns out that Boolean circuits are equivalent in power to such models as well. The fact that all these different ways to define computation lead to equivalent models shows that we are “on the right track”. It justifies the seemingly arbitrary choices that we’ve made of using AND/OR/NOT or NAND as our basic operations, since these choices do not affect the power of our computational model. Equivalence results such as Theorem 3.19 mean that we can easily translate between Boolean circuits, NAND circuits, NAND-CIRC programs and the like. We will use this ability later on in this book, often shifting to the most convenient formulation without making a big deal about it. Hence we will not worry too much about the distinction between, for example, Boolean circuits and NAND-CIRC programs.
In contrast, we will continue to take special care to distinguish between circuits/programs and functions (recall Big Idea 2). A function corresponds to a specification of a computational task, and it is a fundamentally different object than a program or a circuit, which corresponds to the implementation of the task.
Circuits with other gate sets
There is nothing special about AND/OR/NOT or NAND. For every set of functions \(\mathcal{G} = \{ G_0,\ldots,G_{k-1} \}\), we can define a notion of circuits that use elements of \(\mathcal{G}\) as gates, and a notion of a “\(\mathcal{G}\) programming language” where every line involves assigning to a variable foo the result of applying some \(G_i \in \mathcal{G}\) to previously defined or input variables. Specifically, we can make the following definition:
Let \(\mathcal{F} = \{ f_0,\ldots, f_{t-1} \}\) be a finite collection of Boolean functions, such that \(f_i:\{0,1\}^{k_i} \rightarrow \{0,1\}\) for some \(k_i \in \N\). An \(\mathcal{F}\) program is a sequence of lines, each of which assigns to some variable the result of applying some \(f_i \in \mathcal{F}\) to \(k_i\) other variables. As above, we use X[\(i\)] and Y[\(j\)] to denote the input and output variables.
We say that \(\mathcal{F}\) is a universal set of operations (also known as a universal gate set) if there exists a \(\mathcal{F}\) program to compute the function \(\ensuremath{\mathit{NAND}}\).
AON-CIRC programs correspond to \(\{AND,\ensuremath{\mathit{OR}},\ensuremath{\mathit{NOT}}\}\) programs, NAND-CIRC programs corresponds to \(\mathcal{F}\) programs for the set \(\mathcal{F}\) that only contains the \(\ensuremath{\mathit{NAND}}\) function, but we can also define \(\{ \ensuremath{\mathit{IF}}, \ensuremath{\mathit{ZERO}}, \ensuremath{\mathit{ONE}}\}\) programs (see below), or use any other set.
We can also define \(\mathcal{F}\) circuits, which will be directed graphs in which each gate corresponds to applying a function \(f_i \in \mathcal{F}\), and will each have \(k_i\) incoming wires and a single outgoing wire. (If the function \(f_i\) is not symmetric, in the sense that the order of its input matters then we need to label each wire entering a gate as to which parameter of the function it corresponds to.) As in Theorem 3.9, we can show that \(\mathcal{F}\) circuits and \(\mathcal{F}\) programs are equivalent. We have seen that for \(\mathcal{F} = \{ \ensuremath{\mathit{AND}},\ensuremath{\mathit{OR}}, \ensuremath{\mathit{NOT}}\}\), the resulting circuits/programs are equivalent in power to the NAND-CIRC programming language, as we can compute \(\ensuremath{\mathit{NAND}}\) using \(\ensuremath{\mathit{AND}}\)/\(\ensuremath{\mathit{OR}}\)/\(\ensuremath{\mathit{NOT}}\) and vice versa. This turns out to be a special case of a general phenomenon — the universality of \(\ensuremath{\mathit{NAND}}\) and other gate sets — that we will explore more in-depth later in this book.
Let \(\mathcal{F} = \{ \ensuremath{\mathit{IF}} , \ensuremath{\mathit{ZERO}}, \ensuremath{\mathit{ONE}} \}\) where \(\ensuremath{\mathit{ZERO}}:\{0,1\} \rightarrow \{0\}\) and \(\ensuremath{\mathit{ONE}}:\{0,1\} \rightarrow \{1\}\) are the constant zero and one functions,3 and \(\ensuremath{\mathit{IF}}:\{0,1\}^3 \rightarrow \{0,1\}\) is the function that on input \((a,b,c)\) outputs \(b\) if \(a=1\) and \(c\) otherwise. Then \(\mathcal{F}\) is universal.
Indeed, we can demonstrate that \(\{ \ensuremath{\mathit{IF}}, \ensuremath{\mathit{ZERO}}, \ensuremath{\mathit{ONE}} \}\) is universal using the following formula for \(\ensuremath{\mathit{NAND}}\):
There are also some sets \(\mathcal{F}\) that are more restricted in power. For example it can be shown that if we use only AND or OR gates (without NOT) then we do not get an equivalent model of computation. The exercises cover several examples of universal and non-universal gate sets.
Specification vs. implementation (again)
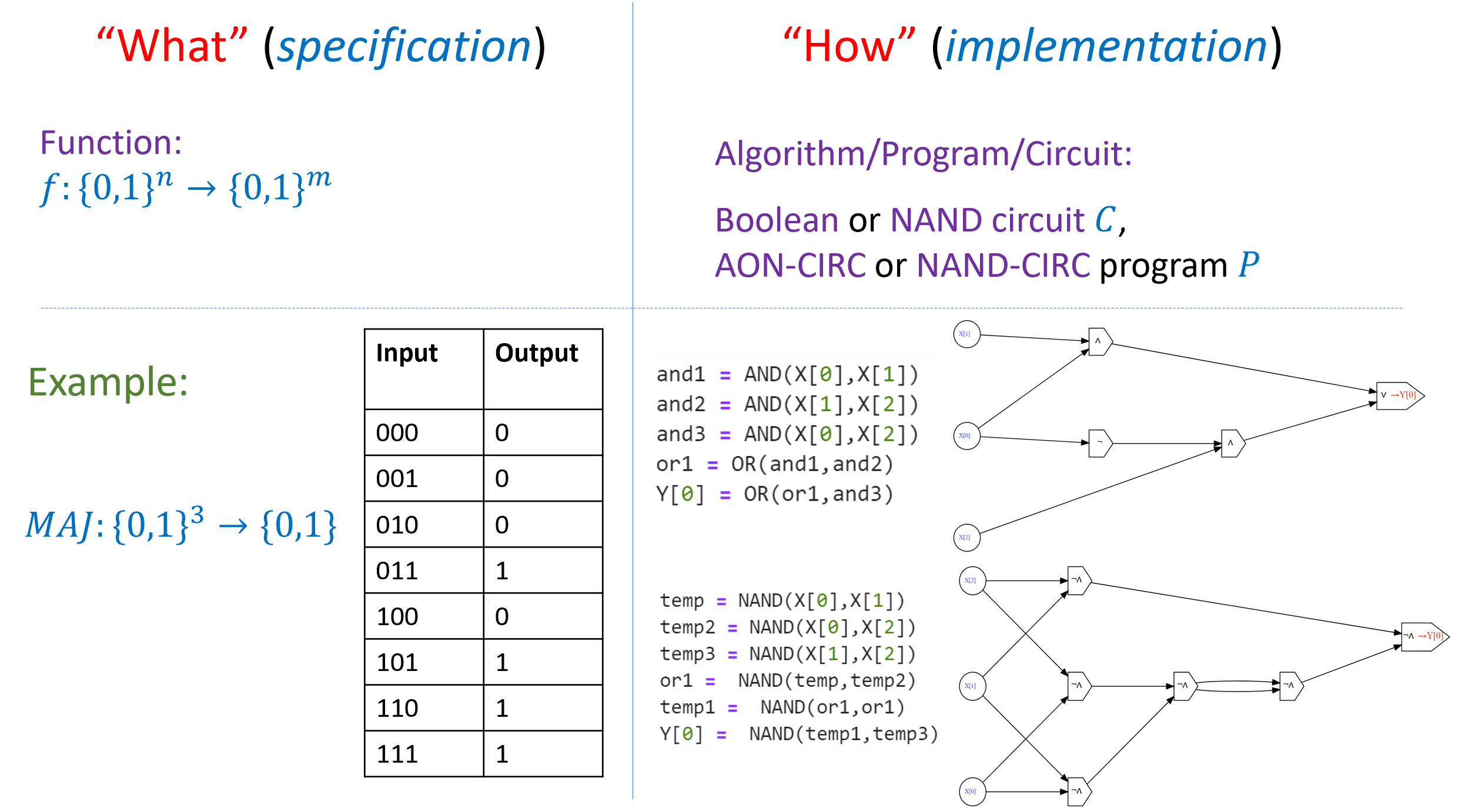
As we discussed in Section 2.6.1, one of the most important distinctions in this book is that of specification versus implementation or separating “what” from “how” (see Figure 3.31). A function corresponds to the specification of a computational task, that is what output should be produced for every particular input. A program (or circuit, or any other way to specify algorithms) corresponds to the implementation of how to compute the desired output from the input. That is, a program is a set of instructions on how to compute the output from the input. Even within the same computational model there can be many different ways to compute the same function. For example, there is more than one NAND-CIRC program that computes the majority function, more than one Boolean circuit to compute the addition function, and so on and so forth.
Confusing specification and implementation (or equivalently functions and programs) is a common mistake, and one that is unfortunately encouraged by the common programming-language terminology of referring to parts of programs as “functions”. However, in both the theory and practice of computer science, it is important to maintain this distinction, and it is particularly important for us in this book.
- An algorithm is a recipe for performing a computation as a sequence of “elementary” or “simple” operations.
- One candidate definition for “elementary” operations is the set \(\ensuremath{\mathit{AND}}\), \(\ensuremath{\mathit{OR}}\) and \(\ensuremath{\mathit{NOT}}\).
- Another candidate definition for an “elementary” operation is the \(\ensuremath{\mathit{NAND}}\) operation. It is an operation that is easily implementable in the physical world in a variety of methods including by electronic transistors.
- We can use \(\ensuremath{\mathit{NAND}}\) to compute many other functions, including majority, increment, and others.
- There are other equivalent choices, including the sets \(\{AND,\ensuremath{\mathit{OR}},\ensuremath{\mathit{NOT}}\}\) and \(\{ \ensuremath{\mathit{IF}}, \ensuremath{\mathit{ZERO}}, \ensuremath{\mathit{ONE}} \}\).
- We can formally define the notion of a function \(F:\{0,1\}^n \rightarrow \{0,1\}^m\) being computable using the NAND-CIRC Programming language.
- For every set of basic operations, the notions of being computable by a circuit and being computable by a straight-line program are equivalent.
Exercises
Give a Boolean circuit (with AND/OR/NOT gates) that computes the function \(\ensuremath{\mathit{CMP}}_8:\{0,1\}^8 \rightarrow \{0,1\}\) such that \(\ensuremath{\mathit{CMP}}_8(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)=1\) if and only if the number represented by \(a_0a_1a_2a_3\) is larger than the number represented by \(b_0b_1b_2b_3\).
Prove that there exists a constant \(c\) such that for every \(n\) there is a Boolean circuit (with AND/OR/NOT gates) \(C\) of at most \(c\cdot n\) gates that computes the function \(\ensuremath{\mathit{CMP}}_{2n}:\{0,1\}^{2n} \rightarrow \{0,1\}\) such that \(\ensuremath{\mathit{CMP}}_{2n}(a_0\cdots a_{n-1} b_0 \cdots b_{n-1})=1\) if and only if the number represented by \(a_0 \cdots a_{n-1}\) is larger than the number represented by \(b_0 \cdots b_{n-1}\).
Prove that the set \(\{ \ensuremath{\mathit{OR}}, \ensuremath{\mathit{NOT}} \}\) is universal, in the sense that one can compute NAND using these gates.
Prove that for every \(n\)-bit input circuit \(C\) that contains only AND and OR gates, as well as gates that compute the constant functions \(0\) and \(1\), \(C\) is monotone, in the sense that if \(x,x' \in \{0,1\}^n\), \(x_i \leq x'_i\) for every \(i\in [n]\), then \(C(x) \leq C(x')\).
Conclude that the set \(\{ \ensuremath{\mathit{AND}}, \ensuremath{\mathit{OR}}, 0, 1\}\) is not universal.
Prove that for every \(n\)-bit input circuit \(C\) that contains only XOR gates, as well as gates that compute the constant functions \(0\) and \(1\), \(C\) is affine or linear modulo two, in the sense that there exists some \(a\in \{0,1\}^n\) and \(b\in \{0,1\}\) such that for every \(x\in \{0,1\}^n\), \(C(x) = \sum_{i=0}^{n-1}a_ix_i + b \mod 2\).
Conclude that the set \(\{ \ensuremath{\mathit{XOR}} , 0 , 1\}\) is not universal.
Let \(\ensuremath{\mathit{MAJ}}:\{0,1\}^3 \rightarrow \{0,1\}\) be the majority function. Prove that \(\{ \ensuremath{\mathit{MAJ}},\ensuremath{\mathit{NOT}}, 1 \}\) is a universal set of gates.
Prove that \(\{ \ensuremath{\mathit{MAJ}},\ensuremath{\mathit{NOT}} \}\) is not a universal set. See footnote for hint.4
Let \(\ensuremath{\mathit{NOR}}:\{0,1\}^2 \rightarrow \{0,1\}\) defined as \(\ensuremath{\mathit{NOR}}(a,b) = \ensuremath{\mathit{NOT}}(\ensuremath{\mathit{OR}}(a,b))\). Prove that \(\{ \ensuremath{\mathit{NOR}} \}\) is a universal set of gates.
Prove that \(\{ \ensuremath{\mathit{LOOKUP}}_1,0,1 \}\) is a universal set of gates where \(0\) and \(1\) are the constant functions and \(\ensuremath{\mathit{LOOKUP}}_1:\{0,1\}^3 \rightarrow \{0,1\}\) satisfies \(\ensuremath{\mathit{LOOKUP}}_1(a,b,c)\) equals \(a\) if \(c=0\) and equals \(b\) if \(c=1\).
Prove that for every subset \(B\) of the functions from \(\{0,1\}^k\) to \(\{0,1\}\), if \(B\) is universal then there is a \(B\)-circuit of at most \(O(1)\) gates to compute the \(\ensuremath{\mathit{NAND}}\) function (you can start by showing that there is a \(B\) circuit of at most \(O(k^{16})\) gates).5
Prove that for every NAND circuit of size \(s\) with \(n\) inputs and \(m\) outputs, \(s \geq \min \{ n/2 , m \}\). See footnote for hint.6
Prove that there is some constant \(c\) such that for every \(n>1\), and integers \(a_0,\ldots,a_{n-1},b \in \{-2^n,-2^n+1,\ldots,-1,0,+1,\ldots,2^n\}\), there is a NAND circuit with at most \(c n^4\) gates that computes the threshold function \(f_{a_0,\ldots,a_{n-1},b}:\{0,1\}^n \rightarrow \{0,1\}\) that on input \(x\in \{0,1\}^n\) outputs \(1\) if and only if \(\sum_{i=0}^{n-1} a_i x_i > b\).
We say that a function \(f:\mathbb{R}^2 \rightarrow \mathbb{R}\) is a NAND approximator if it has the following property: for every \(a,b \in \mathbb{R}\), if \(\min\{|a|,|1-a|\}\leq 1/3\) and \(\min \{ |b|,|1-b| \}\leq 0.1\) then \(|f(a,b) - \ensuremath{\mathit{NAND}}(\lfloor a \rceil, \lfloor b \rceil)| \leq 0.1\) where we denote by \(\lfloor x \rceil\) the integer closest to \(x\). That is, if \(a,b\) are within a distance \(1/3\) to \(\{0,1\}\) then we want \(f(a,b)\) to equal the \(\ensuremath{\mathit{NAND}}\) of the values in \(\{0,1\}\) that are closest to \(a\) and \(b\) respectively. Otherwise, we do not care what the output of \(f\) is on \(a\) and \(b\).
In this exercise you will show that you can construct a NAND approximator from many common activation functions used in deep neural networks. As a corollary you will obtain that deep neural networks can simulate NAND circuits. Since NAND circuits can also simulate deep neural networks, these two computational models are equivalent to one another.
Show that there is a NAND approximator \(f\) defined as \(f(a,b) = L(\ensuremath{\mathit{DR}}eLU(L'(a,b)))\) where \(L':\mathbb{R}^2 \rightarrow \mathbb{R}\) is an affine function (of the form \(L'(a,b)=\alpha a + \beta b + \gamma\) for some \(\alpha,\beta,\gamma \in \mathbb{R}\)), \(L\) is an affine function (of the form \(L(y) = \alpha y + \beta\) for \(\alpha,\beta \in \mathbb{R}\)), and \(\ensuremath{\mathit{DR}}eLU:\mathbb{R} \rightarrow \mathbb{R}\), is the function defined as \(\ensuremath{\mathit{DR}}eLU(x) = \min(1,\max(0,x))\). Note that \(\ensuremath{\mathit{DR}}eLU(x) = 1-ReLU(1-ReLU(x))\) where \(ReLU(x)=\max(x,0)\) is the rectified linear unit activation function.
Show that there is a NAND approximator \(f\) defined as \(f(a,b) = L(sigmoid(L'(a,b)))\) where \(L',L\) are affine as above and \(sigmoid:\mathbb{R} \rightarrow \mathbb{R}\) is the function defined as \(sigmoid(x) = e^x/(e^x+1)\).
Show that there is a NAND approximator \(f\) defined as \(f(a,b) = L(tanh(L'(a,b)))\) where \(L',L\) are affine as above and \(tanh:\mathbb{R} \rightarrow \mathbb{R}\) is the function defined as \(tanh(x) = (e^x-e^{-x})/(e^x+e^{-x})\).
Prove that for every NAND-circuit \(C\) with \(n\) inputs and one output that computes a function \(g:\{0,1\}^n \rightarrow \{0,1\}\), if we replace every gate of \(C\) with a NAND-approximator and then invoke the resulting circuit on some \(x\in \{0,1\}^n\), the output will be a number \(y\) such that \(|y-g(x)|\leq 1/3\).
Prove that there is some constant \(c\) such that for every \(n>1\), there is a NAND circuit of at most \(c\cdot n\) gates that computes the majority function on \(n\) input bits \(\ensuremath{\mathit{MAJ}}_n:\{0,1\}^n \rightarrow \{0,1\}\). That is \(\ensuremath{\mathit{MAJ}}_n(x)=1\) iff \(\sum_{i=0}^{n-1}x_i > n/2\). See footnote for hint.7
Prove that for every \(f:\{0,1\}^n \rightarrow \{0,1\}\), if there is a Boolean circuit \(C\) of \(s\) gates that computes \(f\) then there is a Boolean circuit \(C'\) of at most \(s\) gates such that in the minimal layering of \(C'\), the output gate of \(C'\) is placed in the last layer. See footnote for hint.8
Biographical notes
The excerpt from Al-Khwarizmi’s book is from “The Algebra of Ben-Musa”, Fredric Rosen, 1831.
Charles Babbage (1791-1871) was a visionary scientist, mathematician, and inventor (see (Swade, 2002) (Collier, MacLachlan, 2000) ). More than a century before the invention of modern electronic computers, Babbage realized that computation can be in principle mechanized. His first design for a mechanical computer was the difference engine that was designed to do polynomial interpolation. He then designed the analytical engine which was a much more general machine and the first prototype for a programmable general-purpose computer. Unfortunately, Babbage was never able to complete the design of his prototypes. One of the earliest people to realize the engine’s potential and far-reaching implications was Ada Lovelace (see the notes for Chapter 7).
Boolean algebra was first investigated by Boole and DeMorgan in the 1840’s (Boole, 1847) (De Morgan, 1847) . The definition of Boolean circuits and connection to electrical relay circuits was given in Shannon’s Masters Thesis (Shannon, 1938) . (Howard Gardener called Shannon’s thesis “possibly the most important, and also the most famous, master’s thesis of the [20th] century”.) Savage’s book (Savage, 1998) , like this one, introduces the theory of computation starting with Boolean circuits as the first model. Jukna’s book (Jukna, 2012) contains a modern in-depth exposition of Boolean circuits, see also (Wegener, 1987) .
The NAND function was shown to be universal by Sheffer (Sheffer, 1913) , though this also appears in the earlier work of Peirce, see (Burks, 1978) . Whitehead and Russell used NAND as the basis for their logic in their magnum opus Principia Mathematica (Whitehead, Russell, 1912) . In her Ph.D thesis, Ernst (Ernst, 2009) investigates empirically the minimal NAND circuits for various functions. Nisan and Shocken’s book (Nisan, Schocken, 2005) builds a computing system starting from NAND gates and ending with high-level programs and games (“NAND to Tetris”); see also the website nandtotetris.org.
We defined the size of a Boolean circuit in Definition 3.5 to be the number of gates it contains. This is one of two conventions used in the literature. The other convention is to define the size as the number of wires (equivalent to the number of gates plus the number of inputs). This makes very little difference in almost all settings, but can affect the circuit size complexity of some “pathological examples” of functions such as the constant zero function that do not depend on much of their inputs.
- ↩
Having parallel edges means an AND or OR gate \(u\) can have both its in-neighbors be the same gate \(v\). Since \(\ensuremath{\mathit{AND}}(a,a)=\ensuremath{\mathit{OR}}(a,a)=a\) for every \(a\in \{0,1\}\), such parallel edges don’t help in computing new values in circuits with AND/OR/NOT gates. However, we will see circuits with more general sets of gates later on.
- ↩
For example the C programming language specification takes more than 500 pages.
- ↩
One can also define these functions as taking a length zero input. This makes no difference for the computational power of the model.
- ↩
Hint: Use the fact that \(\ensuremath{\mathit{MAJ}}(\overline{a},\overline{b},\overline{c}) = \overline{MAJ(a,b,c)}\) to prove that every \(f:\{0,1\}^n \rightarrow \{0,1\}\) computable by a circuit with only \(\ensuremath{\mathit{MAJ}}\) and \(\ensuremath{\mathit{NOT}}\) gates satisfies \(f(0,0,\ldots,0) \neq f(1,1,\ldots,1)\). Thanks to Nathan Brunelle and David Evans for suggesting this exercise.
- ↩
Thanks to Alec Sun and Simon Fischer for comments on this problem.
- ↩
Hint: Use the conditions of Definition 3.5 stipulating that every input vertex has at least one out-neighbor and there are exactly \(m\) output gates. See also Remark 3.7.
- ↩
One approach to solve this is using recursion and analyzing it using the so called “Master Theorem”.
- ↩
Hint: Vertices in layers beyond the output can be safely removed without changing the functionality of the circuit.
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 12/06/2023 00:07:40
Copyright 2023, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.