See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below

★ See also the PDF version of this chapter (better formatting/references) ★

Introduction

  • Introduce and motivate the study of computation for its own sake, irrespective of particular implementations.
  • The notion of an algorithm and some of its history.
  • Algorithms as not just tools, but also ways of thinking and understanding.
  • Taste of Big-\(O\) analysis and the surprising creativity in the design of efficient algorithms.

“Computer Science is no more about computers than astronomy is about telescopes”, attributed to Edsger Dijkstra.1

“Hackers need to understand the theory of computation about as much as painters need to understand paint chemistry.”, Paul Graham 2003.2

“The subject of my talk is perhaps most directly indicated by simply asking two questions: first, is it harder to multiply than to add? and second, why?…I (would like to) show that there is no algorithm for multiplication computationally as simple as that for addition, and this proves something of a stumbling block.”, Alan Cobham, 1964

One of the ancient Babylonians’ greatest innovations is the place-value number system. The place-value system represents numbers as sequences of digits where the position of each digit determines its value.

This is opposed to a system like Roman numerals, where every digit has a fixed value regardless of position. For example, the average distance to the moon is approximately 259,956 Roman miles. In standard Roman numerals, that would be

MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMDCCCCLVI

Writing the distance to the sun in Roman numerals would require about 100,000 symbols; it would take a 50-page book to contain this single number!

For someone who thinks of numbers in an additive system like Roman numerals, quantities like the distance to the moon or sun are not merely large—they are unspeakable: they cannot be expressed or even grasped. It’s no wonder that Eratosthenes, the first to calculate the earth’s diameter (up to about ten percent error), and Hipparchus, the first to calculate the distance to the moon, used not a Roman-numeral type system but the Babylonian sexagesimal (base 60) place-value system.

Integer multiplication: an example of an algorithm

In the language of Computer Science, the place-value system for representing numbers is known as a data structure: a set of instructions, or “recipe”, for representing objects as symbols. An algorithm is a set of instructions, or “recipe”, for performing operations on such representations. Data structures and algorithms have enabled amazing applications that have transformed human society, but their importance goes beyond their practical utility. Structures from computer science, such as bits, strings, graphs, and even the notion of a program itself, as well as concepts such as universality and replication, have not just found (many) practical uses but contributed a new language and a new way to view the world.

In addition to coming up with the place-value system, the Babylonians also invented the “standard algorithms” that we were all taught in elementary school for adding and multiplying numbers. These algorithms have been essential throughout the ages for people using abaci, papyrus, or pencil and paper, but in our computer age, do they still serve any purpose beyond torturing third-graders? To see why these algorithms are still very much relevant, let us compare the Babylonian digit-by-digit multiplication algorithm (“grade-school multiplication”) with the naive algorithm that multiplies numbers through repeated addition. We start by formally describing both algorithms, see Algorithm 0.1 and Algorithm 0.2.

Algorithm 0.1 Multiplication via repeated addition

Input: Non-negative integers \(x,y\)

Output: Product \(x\cdot y\)

Let \(result \leftarrow 0\).

for{\(i=1,\ldots,y\)}

\(result \leftarrow result + x\)

endfor

return \(result\)

Algorithm 0.2 Grade-school multiplication

Input: Non-negative integers \(x,y\)

Output: Product \(x\cdot y\)

Write \(x=x_{n-1}x_{n-2}\cdots x_0\) and \(y = y_{m-1}y_{m-2}\cdots y_0\) in decimal place-value notation. # \(x_0\) is the ones digit of \(x\), \(x_1\) is the tens digit, etc.

Let \(result \leftarrow 0\)

for{\(i=0,\ldots,n-1\)}

for{\(j=0,\ldots,m-1\)}

\(result \leftarrow result + 10^{i+j}\cdot x_i \cdot y_j\)

endfor

endfor

return \(result\)

Both Algorithm 0.1 and Algorithm 0.2 assume that we already know how to add numbers, and Algorithm 0.2 also assumes that we can multiply a number by a power of \(10\) (which is, after all, a simple shift). Suppose that \(x\) and \(y\) are two integers of \(n=20\) decimal digits each. (This roughly corresponds to 64 binary digits, which is a common size in many programming languages.) Computing \(x \cdot y\) using Algorithm 0.1 entails adding \(x\) to itself \(y\) times which entails (since \(y\) is a \(20\)-digit number) at least \(10^{19}\) additions. In contrast, the grade-school algorithm (i.e., Algorithm 0.2) involves \(n^2\) shifts and single-digit products, and so at most \(2n^2 = 800\) single-digit operations. To understand the difference, consider that a grade-schooler can perform a single-digit operation in about 2 seconds, and so would require about \(1,600\) seconds (about half an hour) to compute \(x\cdot y\) using Algorithm 0.2. In contrast, even though it is more than a billion times faster than a human, if we used Algorithm 0.1 to compute \(x\cdot y\) using a modern PC, it would take us \(10^{20}/10^9 = 10^{11}\) seconds (which is more than three millennia!) to compute the same result.

Computers have not made algorithms obsolete. On the contrary, the vast increase in our ability to measure, store, and communicate data has led to much higher demand for developing better and more sophisticated algorithms that empower us to make better decisions based on these data. We also see that in no small extent the notion of algorithm is independent of the actual computing device that executes it. The digit-by-digit multiplication algorithm is vastly better than iterated addition, regardless of whether the technology we use to implement it is a silicon-based chip, or a third-grader with pen and paper.

Theoretical computer science is concerned with the inherent properties of algorithms and computation; namely, those properties that are independent of current technology. We ask some questions that were already pondered by the Babylonians, such as “what is the best way to multiply two numbers?”, but also questions that rely on cutting-edge science such as “could we use the effects of quantum entanglement to factor numbers faster?”.

A full description of an algorithm has three components:

  • Specification: What is the task that the algorithm performs (e.g., multiplication in the case of Algorithm 0.1 and Algorithm 0.2.)

  • Implementation: How is the task accomplished: what is the sequence of instructions to be performed. Even though Algorithm 0.1 and Algorithm 0.2 perform the same computational task (i.e., they have the same specification), they do it in different ways (i.e., they have different implementations).

  • Analysis: Why does this sequence of instructions achieve the desired task. A full description of Algorithm 0.1 and Algorithm 0.2 will include a proof for each one of these algorithms that on input \(x,y\), the algorithm does indeed output \(x\cdot y\).

Often as part of the analysis we show that the algorithm is not only correct but also efficient. That is, we want to show that not only will the algorithm compute the desired task, but will do so in a prescribed number of operations. For example Algorithm 0.2 computes the multiplication function on inputs of \(n\) digits using \(O(n^2)\) operations, while Algorithm 0.4 (described below) computes the same function using \(O(n^{1.6})\) operations. (We define the \(O\) notations used here in Section 1.4.8.)

Extended Example: A faster way to multiply (optional)

Once you think of the standard digit-by-digit multiplication algorithm, it seems like the ``obviously best’’ way to multiply numbers. In 1960, the famous mathematician Andrey Kolmogorov organized a seminar at Moscow State University in which he conjectured that every algorithm for multiplying two \(n\) digit numbers would require a number of basic operations that is proportional to \(n^2\) (\(\Omega(n^2)\) operations, using \(O\)-notation as defined in Chapter 1). In other words, Kolmogorov conjectured that in any multiplication algorithm, doubling the number of digits would quadruple the number of basic operations required. A young student named Anatoly Karatsuba was in the audience, and within a week he disproved Kolmogorov’s conjecture by discovering an algorithm that requires only about \(Cn^{1.6}\) operations for some constant \(C\). Such a number becomes much smaller than \(n^2\) as \(n\) grows and so for large \(n\) Karatsuba’s algorithm is superior to the grade-school one. (For example, Python’s implementation switches from the grade-school algorithm to Karatsuba’s algorithm for numbers that are 1000 bits or larger.) While the difference between an \(O(n^{1.6})\) and an \(O(n^2)\) algorithm can be sometimes crucial in practice (see Section 0.3 below), in this book we will mostly ignore such distinctions. However, we describe Karatsuba’s algorithm below since it is a good example of how algorithms can often be surprising, as well as a demonstration of the analysis of algorithms, which is central to this book and to theoretical computer science at large.

Karatsuba’s algorithm is based on a faster way to multiply two-digit numbers. Suppose that \(x,y \in [100]=\{0,\ldots, 99 \}\) are a pair of two-digit numbers. Let’s write \(\overline{x}\) for the “tens” digit of \(x\), and \(\underline{x}\) for the “ones” digit, so that \(x = 10\overline{x} + \underline{x}\), and write similarly \(y = 10\overline{y} + \underline{y}\) for \(\overline{x},\underline{x},\overline{y},\underline{y} \in [10]\). The grade-school algorithm for multiplying \(x\) and \(y\) is illustrated in Figure 1.

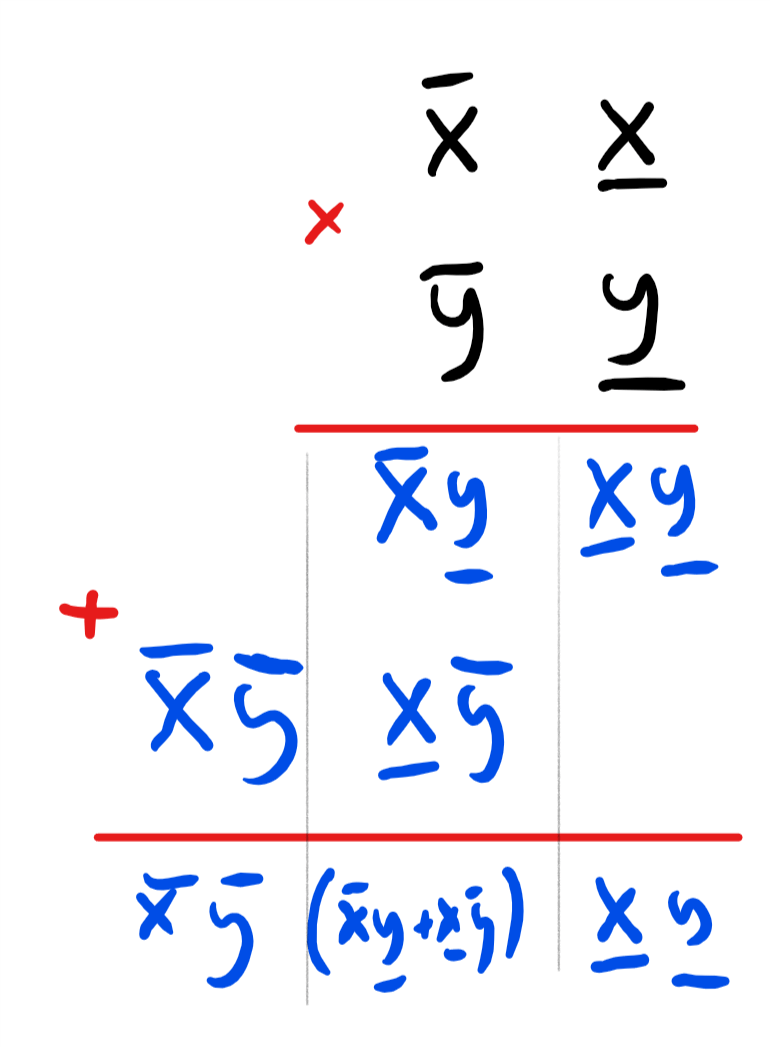
1: The grade-school multiplication algorithm illustrated for multiplying \(x=10\overline{x}+\underline{x}\) and \(y=10\overline{y}+\underline{y}\). It uses the formula \((10\overline{x}+\underline{x}) \times (10 \overline{y}+\underline{y}) = 100\overline{x}\overline{y}+10(\overline{x}\underline{y} + \underline{x}\overline{y}) + \underline{x}\underline{y}\).

The grade-school algorithm can be thought of as transforming the task of multiplying a pair of two-digit numbers into four single-digit multiplications via the formula

\[ (10\overline{x}+\underline{x}) \times (10 \overline{y}+\underline{y}) = 100\overline{x}\overline{y}+10(\overline{x}\underline{y} + \underline{x}\overline{y}) + \underline{x}\underline{y} \;\;(1) \]

Generally, in the grade-school algorithm doubling the number of digits in the input results in quadrupling the number of operations, leading to an \(O(n^2)\) times algorithm. In contrast, Karatsuba’s algorithm is based on the observation that we can express Equation 1 also as

\[ (10\overline{x}+\underline{x}) \times (10 \overline{y}+\underline{y}) = (100-10)\overline{x}\overline{y}+10\left[(\overline{x}+\underline{x})(\overline{y}+\underline{y})\right] -(10-1)\underline{x}\underline{y} \;\;(2) \]

which reduces multiplying the two-digit number \(x\) and \(y\) to computing the following three simpler products: \(\overline{x}\overline{y}\), \(\underline{x}\underline{y}\) and \((\overline{x}+\underline{x})(\overline{y}+\underline{y})\). By repeating the same strategy recursively, we can reduce the task of multiplying two \(n\)-digit numbers to the task of multiplying three pairs of \(\floor{n/2}+1\) digit numbers.3 Since every time we double the number of digits we triple the number of operations, we will be able to multiply numbers of \(n=2^\ell\) digits using about \(3^\ell = n^{\log_2 3} \sim n^{1.585}\) operations.

The above is the intuitive idea behind Karatsuba’s algorithm, but is not enough to fully specify it. A complete description of an algorithm entails a precise specification of its operations together with its analysis: proof that the algorithm does in fact do what it’s supposed to do. The operations of Karatsuba’s algorithm are detailed in Algorithm 0.4, while the analysis is given in Lemma 0.5 and Lemma 0.6.

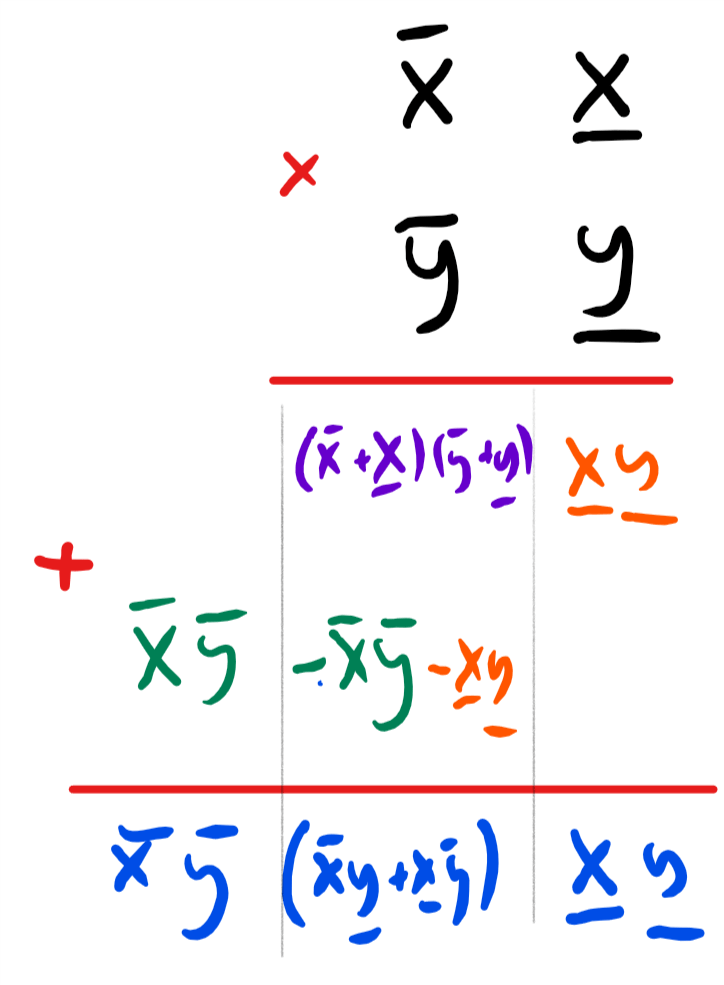
2: Karatsuba’s multiplication algorithm illustrated for multiplying \(x=10\overline{x}+\underline{x}\) and \(y=10\overline{y}+\underline{y}\). We compute the three orange, green and purple products \(\underline{x}\underline{y}\), \(\overline{x}\overline{y}\) and \((\overline{x}+\underline{x})(\overline{y}+\underline{y})\) and then add and subtract them to obtain the result.
3: Running time of Karatsuba’s algorithm vs. the grade-school algorithm. (Python implementation available online.) Note the existence of a “cutoff” length, where for sufficiently large inputs Karatsuba becomes more efficient than the grade-school algorithm. The precise cutoff location varies by implementation and platform details, but will always occur eventually.

Algorithm 0.4 Karatsuba multiplication

Input: non-negative integers \(x,y\) each of at most \(n\) digits

Output: \(x\cdot y\)

Procedure \(\mathsf{Karatsuba}\)(\(x\),\(y\))

if {\(n \leq 4\)} return \(x\cdot y\) ;

Let \(m = \lfloor n/2 \rfloor\)

Write \(x= 10^{m}\overline{x} + \underline{x}\) and \(y= 10^{m}\overline{y}+ \underline{y}\)

\(A \leftarrow \mathsf{Karatsuba}(\overline{x),\overline{y}}\)

\(B \leftarrow \mathsf{Karatsuba}(\overline{x)+\underline{x},\overline{y}+\underline{y}}\)

\(C \leftarrow \mathsf{Karatsuba}(\underline{x),\underline{y}}\)

return \((10^n-10^m)\cdot A + 10^m \cdot B +(1-10^m)\cdot C\)

endproc

Algorithm 0.4 is only half of the full description of Karatsuba’s algorithm. The other half is the analysis, which entails proving that (1) Algorithm 0.4 indeed computes the multiplication operation and (2) it does so using \(O(n^{\log_2 3})\) operations. We now turn to showing both facts:

For every non-negative integers \(x,y\), when given input \(x,y\) Algorithm 0.4 will output \(x\cdot y\).

Let \(n\) be the maximum number of digits of \(x\) and \(y\). We prove the lemma by induction on \(n\). The base case is \(n \leq 4\) where the algorithm returns \(x\cdot y\) by definition. (It does not matter which algorithm we use to multiply four-digit numbers - we can even use repeated addition.) Otherwise, if \(n>4\), we define \(m = \floor{n/2}\), and write \(x= 10^{m}\overline{x} + \underline{x}\) and \(y= 10^{m}\overline{y}+ \underline{y}\).

Plugging this into \(x\cdot y\), we get

\[ x \cdot y = 10^{2m} \overline{x}\overline{y} + 10^{m}(\overline{x}\underline{y} +\underline{x}\overline{y}) + \underline{x}\underline{y} \;. \;\;(3) \]

Rearranging the terms we see that

\[ x\cdot y = 10^{2m}\overline{x}\overline{y} + 10^{m}\left[ (\overline{x}+\underline{x})(\overline{y}+\underline{y}) - \underline{x}\underline{y} - \overline{x}\overline{y} \right] + \underline{x}\underline{y} \;. \;\;(4) \]
since the numbers \(\underline{x}\),\(\overline{x}\), \(\underline{y}\),\(\overline{y}\),\(\overline{x}+\underline{x}\),\(\overline{y}+\underline{y}\) all have at most \(m+2<n\) digits, the induction hypothesis implies that the values \(A,B,C\) computed by the recursive calls will satisfy \(A=\overline{x}\overline{y}\), \(B=(\overline{x}+\underline{x})(\overline{y}+\underline{y})\) and \(C=\underline{x}\underline{y}\). Plugging this into Equation 4 we see that \(x\cdot y\) equals the value \((10^{2m}-10^m)\cdot A + 10^m \cdot B +(1-10^m)\cdot C\) computed by Algorithm 0.4.

If \(x,y\) are integers of at most \(n\) digits, Algorithm 0.4 will take \(O(n^{\log_2 3})\) operations on input \(x,y\).

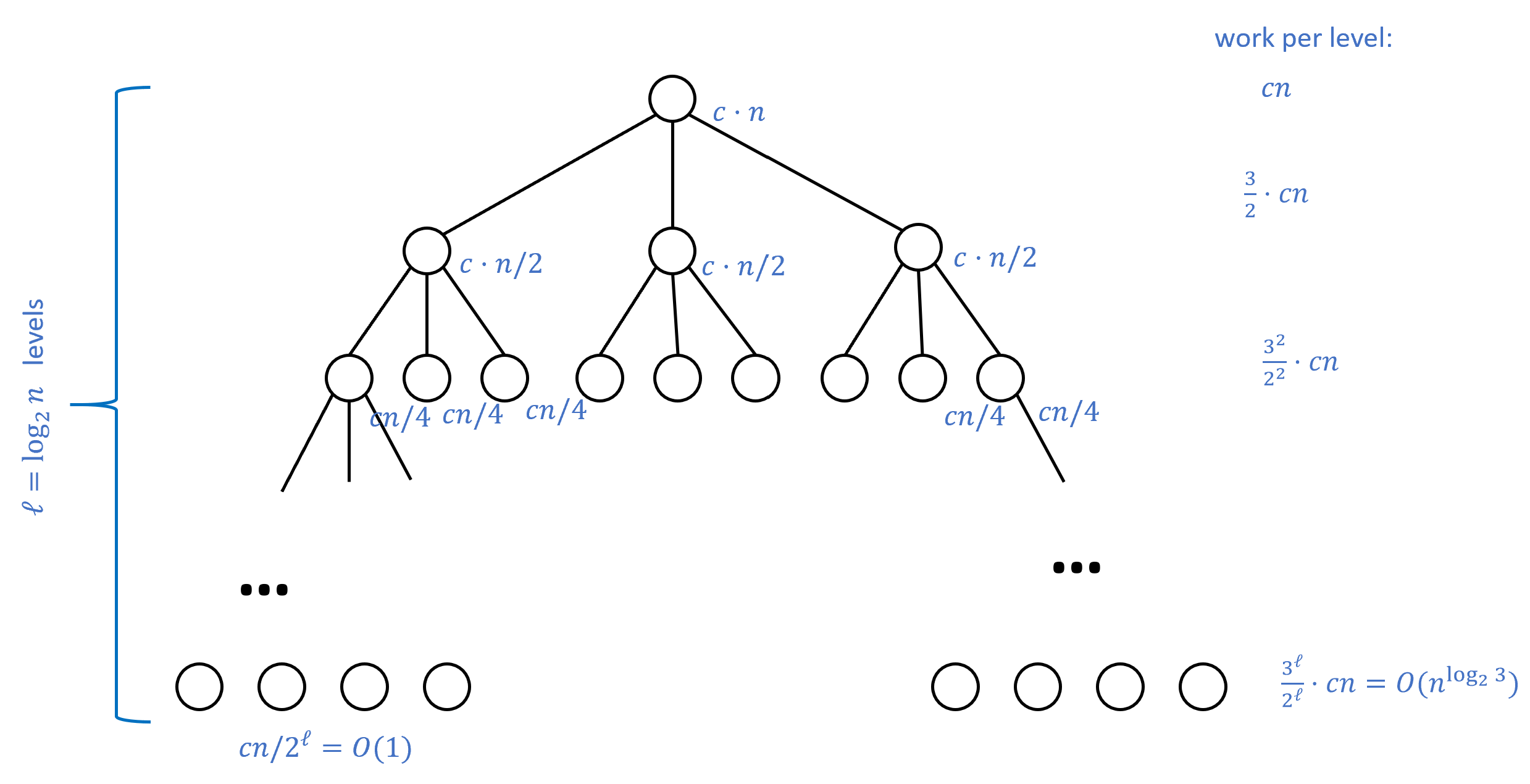
Figure 2 illustrates the idea behind the proof, which we only sketch here, leaving filling out the details as Exercise 0.4. The proof is again by induction. We define \(T(n)\) to be the maximum number of steps that Algorithm 0.4 takes on inputs of length at most \(n\). Since in the base case \(n\leq 4\), Exercise 0.4 performs a constant number of computation, we know that \(T(4) \leq c\) for some constant \(c\) and for \(n>4\), it satisfies the recursive equation

\[ T(n) \leq 3T(\floor{n/2}+1) + c' n \;\;(5) \]
for some constant \(c'\) (using the fact that addition can be done in \(O(n)\) operations).

The recursive equation Equation 5 solves to \(O(n^{\log_2 3})\). The intuition behind this is presented in Figure 2, and this is also a consequence of the so-called “Master Theorem” on recurrence relations. As mentioned above, we leave completing the proof to the reader as Exercise 0.4.

4: Karatsuba’s algorithm reduces an \(n\)-bit multiplication to three \(n/2\)-bit multiplications, which in turn are reduced to nine \(n/4\)-bit multiplications and so on. We can represent the computational cost of all these multiplications in a \(3\)-ary tree of depth \(\log_2 n\), where at the root the extra cost is \(cn\) operations, at the first level the extra cost is \(c(n/2)\) operations, and at each of the \(3^i\) nodes of level \(i\), the extra cost is \(c(n/2^i)\). The total cost is \(cn\sum_{i=0}^{\log_2 n} (3/2)^i \leq 10cn^{\log_2 3}\) by the formula for summing a geometric series.

Karatsuba’s algorithm is by no means the end of the line for multiplication algorithms. In the 1960’s, Toom and Cook extended Karatsuba’s ideas to get an \(O(n^{\log_k (2k-1)})\) time multiplication algorithm for every constant \(k\). In 1971, Schönhage and Strassen got even better algorithms using the Fast Fourier Transform; their idea was to somehow treat integers as “signals” and do the multiplication more efficiently by moving to the Fourier domain. (The Fourier transform is a central tool in mathematics and engineering, used in a great many applications; if you have not seen it yet, you are likely to encounter it at some point in your studies.) In the years that followed researchers kept improving the algorithm, and only very recently Harvey and Van Der Hoeven managed to obtain an \(O(n \log n)\) time algorithm for multiplication (though it only starts beating the Schönhage-Strassen algorithm for truly astronomical numbers). Yet, despite all this progress, we still don’t know whether or not there is an \(O(n)\) time algorithm for multiplying two \(n\) digit numbers!

(This book contains many “advanced” or “optional” notes and sections. These may assume background that not every student has, and can be safely skipped over as none of the future parts depends on them.)

Ideas similar to Karatsuba’s can be used to speed up matrix multiplications as well. Matrices are a powerful way to represent linear equations and operations, widely used in numerous applications of scientific computing, graphics, machine learning, and many many more.

One of the basic operations one can do with two matrices is to multiply them. For example, if \(x = \begin{pmatrix} x_{0,0} & x_{0,1}\\ x_{1,0}& x_{1,1} \end{pmatrix}\) and \(y = \begin{pmatrix} y_{0,0} & y_{0,1}\\ y_{1,0}& y_{1,1} \end{pmatrix}\) then the product of \(x\) and \(y\) is the matrix \(\begin{pmatrix} x_{0,0}y_{0,0} + x_{0,1}y_{1,0} & x_{0,0}y_{0,1} + x_{0,1}y_{1,1}\\ x_{1,0}y_{0,0}+x_{1,1}y_{1,0} & x_{1,0}y_{0,1}+x_{1,1}y_{1,1} \end{pmatrix}\). You can see that we can compute this matrix by eight products of numbers.

Now suppose that \(n\) is even and \(x\) and \(y\) are a pair of \(n\times n\) matrices which we can think of as each composed of four \((n/2)\times (n/2)\) blocks \(x_{0,0},x_{0,1},x_{1,0},x_{1,1}\) and \(y_{0,0},y_{0,1},y_{1,0},y_{1,1}\). Then the formula for the matrix product of \(x\) and \(y\) can be expressed in the same way as above, just replacing products \(x_{a,b}y_{c,d}\) with matrix products, and addition with matrix addition. This means that we can use the formula above to give an algorithm that doubles the dimension of the matrices at the expense of increasing the number of operations by a factor of \(8\), which for \(n=2^\ell\) results in \(8^\ell = n^3\) operations.

In 1969 Volker Strassen noted that we can compute the product of a pair of two-by-two matrices using only seven products of numbers by observing that each entry of the matrix \(xy\) can be computed by adding and subtracting the following seven terms: \(t_1 = (x_{1,0}+x_{1,1})(y_{0,0}+y_{1,1})\), \(t_2 = (x_{0,0}+x_{1,1})y_{0,0}\), \(t_3 = x_{0,0}(y_{0,1}-y_{1,1})\), \(t_4 = x_{1,1}(y_{0,1}-y_{0,0})\), \(t_5 = (x_{0,0}+x_{0,1})y_{1,1}\), \(t_6 = (x_{1,0}-x_{0,0})(y_{1,0}+y_{0,1})\), \(t_7 = (x_{0,1}-x_{1,1})(y_{1,0}+y_{1,1})\). Indeed, one can verify that \(xy = \begin{pmatrix} t_1 + t_4 - t_5 + t_7 & t_3 + t_5 \\ t_2 +t_4 & t_1 + t_3 - t_2 + t_6 \end{pmatrix}\).

Using this observation, we can obtain an algorithm such that doubling the dimension of the matrices results in increasing the number of operations by a factor of \(7\), which means that for \(n=2^\ell\) the cost is \(7^\ell = n^{\log_2 7} \sim n^{2.807}\). A long sequence of work has since improved this algorithm, and the current record has a running time of about \(O(n^{2.373})\). However, unlike the case of integer multiplication, at the moment we don’t know of any algorithm for matrix multiplication that runs in time linear or even close to linear in the size of the input matrices (e.g., an \(O(n^2 polylog(n))\) time algorithm). People have tried to use group representations, which can be thought of as generalizations of the Fourier transform, to obtain faster algorithms, but this effort has not yet succeeded.

Algorithms beyond arithmetic

The quest for better algorithms is by no means restricted to arithmetic tasks such as adding, multiplying or solving equations. Many graph algorithms, including algorithms for finding paths, matchings, spanning trees, cuts, and flows, have been discovered in the last several decades, and this is still an intensive area of research. (For example, the last few years saw many advances in algorithms for the maximum flow problem, borne out of unexpected connections with electrical circuits and linear equation solvers.) These algorithms are being used not just for the “natural” applications of routing network traffic or GPS-based navigation, but also for applications as varied as drug discovery through searching for structures in gene-interaction graphs to computing risks from correlations in financial investments.

Google was founded based on the PageRank algorithm, which is an efficient algorithm to approximate the “principal eigenvector” of (a dampened version of) the adjacency matrix of the web graph. The Akamai company was founded based on a new data structure, known as consistent hashing, for a hash table where buckets are stored at different servers. The backpropagation algorithm, which computes partial derivatives of a neural network in \(O(n)\) instead of \(O(n^2)\) time, underlies many of the recent phenomenal successes of learning deep neural networks. Algorithms for solving linear equations under sparsity constraints, a concept known as compressed sensing, have been used to drastically reduce the amount and quality of data needed to analyze MRI images. This made a critical difference for MRI imaging of cancer tumors in children, where previously doctors needed to use anesthesia to suspend breath during the MRI exam, sometimes with dire consequences.

Even for classical questions, studied through the ages, new discoveries are still being made. For example, for the question of determining whether a given integer is prime or composite, which has been studied since the days of Pythagoras, efficient probabilistic algorithms were only discovered in the 1970s, while the first deterministic polynomial-time algorithm was only found in 2002. For the related problem of actually finding the factors of a composite number, new algorithms were found in the 1980s, and (as we’ll see later in this course) discoveries in the 1990s raised the tantalizing prospect of obtaining faster algorithms through the use of quantum mechanical effects.

Despite all this progress, there are still many more questions than answers in the world of algorithms. For almost all natural problems, we do not know whether the current algorithm is the “best”, or whether a significantly better one is still waiting to be discovered. As alluded to in Cobham’s opening quote for this chapter, even for the basic problem of multiplying numbers we have not yet answered the question of whether there is a multiplication algorithm that is as efficient as our algorithms for addition. But at least we now know the right way to ask it.

On the importance of negative results

Finding better algorithms for problems such as multiplication, solving equations, graph problems, or fitting neural networks to data, is undoubtedly a worthwhile endeavor. But why is it important to prove that such algorithms don’t exist? One motivation is pure intellectual curiosity. Another reason to study impossibility results is that they correspond to the fundamental limits of our world. In other words, impossibility results are laws of nature.

Here are some examples of impossibility results outside computer science (see Section 0.7 for more about these). In physics, the impossibility of building a perpetual motion machine corresponds to the law of conservation of energy. The impossibility of building a heat engine beating Carnot’s bound corresponds to the second law of thermodynamics, while the impossibility of faster-than-light information transmission is a cornerstone of special relativity. In mathematics, while we all learned the formula for solving quadratic equations in high school, the impossibility of generalizing this formula to equations of degree five or more gave birth to group theory. The impossibility of proving Euclid’s fifth axiom from the first four gave rise to non-Euclidean geometries, which ended up crucial for the theory of general relativity.

In an analogous way, impossibility results for computation correspond to “computational laws of nature” that tell us about the fundamental limits of any information processing apparatus, whether based on silicon, neurons, or quantum particles. Moreover, computer scientists found creative approaches to apply computational limitations to achieve certain useful tasks. For example, much of modern Internet traffic is encrypted using the RSA encryption scheme, the security of which relies on the (conjectured) impossibility of efficiently factoring large integers. More recently, the Bitcoin system uses a digital analog of the “gold standard” where, instead of using a precious metal, new currency is obtained by “mining” solutions for computationally difficult problems.

  • The history of algorithms goes back thousands of years; they have been essential to much of human progress and these days form the basis of multi-billion dollar industries, as well as life-saving technologies.
  • There is often more than one algorithm to achieve the same computational task. Finding a faster algorithm can often make a much bigger difference than improving computing hardware.
  • Better algorithms and data structures don’t just speed up calculations, but can yield new qualitative insights.
  • One question we will study is to find out what is the most efficient algorithm for a given problem.
  • To show that an algorithm is the most efficient one for a given problem, we need to be able to prove that it is impossible to solve the problem using a smaller amount of computational resources.

Roadmap to the rest of this book

Often, when we try to solve a computational problem, whether it is solving a system of linear equations, finding the top eigenvector of a matrix, or trying to rank Internet search results, it is enough to use the “I know it when I see it” standard for describing algorithms. As long as we find some way to solve the problem, we are happy and might not care much on the exact mathematical model for our algorithm. But when we want to answer a question such as “does there exist an algorithm to solve the problem \(P\)?” we need to be much more precise.

In particular, we will need to (1) define exactly what it means to solve \(P\), and (2) define exactly what an algorithm is. Even (1) can sometimes be non-trivial but (2) is particularly challenging; it is not at all clear how (and even whether) we can encompass all potential ways to design algorithms. We will consider several simple models of computation, and argue that, despite their simplicity, they do capture all “reasonable” approaches to achieve computing, including all those that are currently used in modern computing devices.

Once we have these formal models of computation, we can try to obtain impossibility results for computational tasks, showing that some problems can not be solved (or perhaps can not be solved within the resources of our universe). Archimedes once said that given a fulcrum and a long enough lever, he could move the world. We will see how reductions allow us to leverage one hardness result into a slew of a great many others, illuminating the boundaries between the computable and uncomputable (or tractable and intractable) problems.

Later in this book we will go back to examining our models of computation, and see how resources such as randomness or quantum entanglement could potentially change the power of our model. In the context of probabilistic algorithms, we will see a glimpse of how randomness has become an indispensable tool for understanding computation, information, and communication. We will also see how computational difficulty can be an asset rather than a hindrance, and be used for the “derandomization” of probabilistic algorithms. The same ideas also show up in cryptography, which has undergone not just a technological but also an intellectual revolution in the last few decades, much of it building on the foundations that we explore in this course.

Theoretical Computer Science is a vast topic, branching out and touching upon many scientific and engineering disciplines. This book provides a very partial (and biased) sample of this area. More than anything, I hope I will manage to “infect” you with at least some of my love for this field, which is inspired and enriched by the connection to practice, but is also deep and beautiful regardless of applications.

Dependencies between chapters

This book is divided into the following parts, see Figure 5.

  • Preliminaries: Introduction, mathematical background, and representing objects as strings.

  • Part I: Finite computation (Boolean circuits): Equivalence of circuits and straight-line programs. Universal gate sets. Existence of a circuit for every function, representing circuits as strings, universal circuit, lower bound on circuit size using the counting argument.

  • Part II: Uniform computation (Turing machines): Equivalence of Turing machines and programs with loops. Equivalence of models (including RAM machines, \(\lambda\) calculus, and cellular automata), configurations of Turing machines, existence of a universal Turing machine, uncomputable functions (including the Halting problem and Rice’s Theorem), Gödel’s incompleteness theorem, restricted computational models (regular and context free languages).

  • Part III: Efficient computation: Definition of running time, time hierarchy theorem, \(\mathbf{P}\) and \(\mathbf{NP}\), \(\mathbf{P_{/poly}}\), \(\mathbf{NP}\) completeness and the Cook-Levin Theorem, space bounded computation.

  • Part IV: Randomized computation: Probability, randomized algorithms, \(\mathbf{BPP}\), amplification, \(\mathbf{BPP} \subseteq \mathbf{P}_{/poly}\), pseudorandom generators and derandomization.

  • Part V: Advanced topics: Cryptography, proofs and algorithms (interactive and zero knowledge proofs, Curry-Howard correspondence), quantum computing.

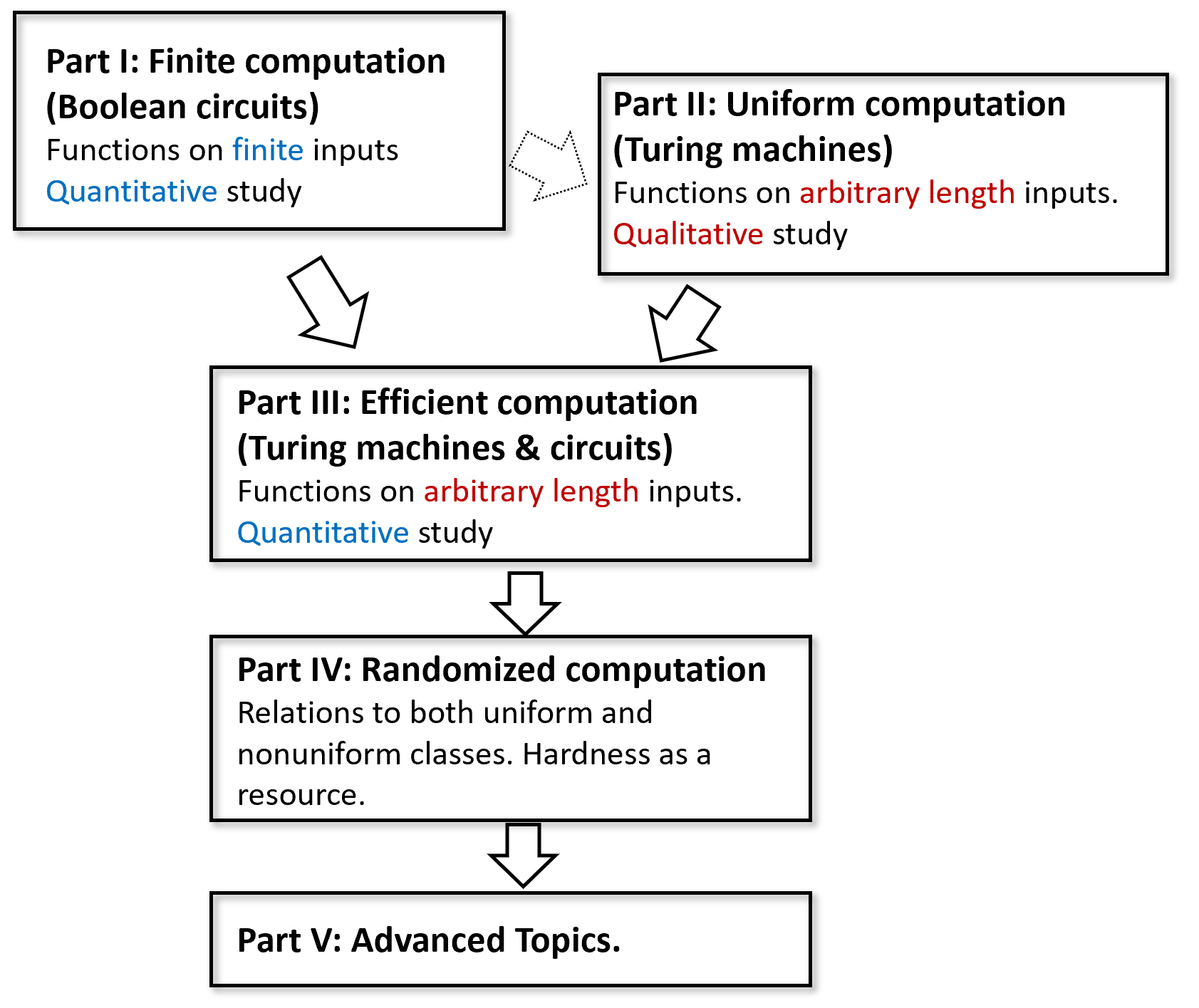
5: The dependency structure of the different parts. Part I introduces the model of Boolean circuits to study finite functions with an emphasis on quantitative questions (how many gates to compute a function). Part II introduces the model of Turing machines to study functions that have unbounded input lengths with an emphasis on qualitative questions (is this function computable or not). Much of Part II does not depend on Part I, as Turing machines can be used as the first computational model. Part III depends on both parts as it introduces a quantitative study of functions with unbounded input length. The more advanced parts IV (randomized computation) and V (advanced topics) rely on the material of Parts I, II and III.

The book largely proceeds in linear order, with each chapter building on the previous ones, with the following exceptions:

  • The topics of \(\lambda\) calculus (Section 8.5 and Section 8.5), Gödel’s incompleteness theorem (Chapter 11), Automata/regular expressions and context-free grammars (Chapter 10), and space-bounded computation (Chapter 17), are not used in the following chapters. Hence you can choose whether to cover or skip any subset of them.

  • Part II (Uniform Computation / Turing Machines) does not have a strong dependency on Part I (Finite computation / Boolean circuits) and it should be possible to teach them in the reverse order with minor modification. Boolean circuits are used Part III (efficient computation) for results such as \(\mathbf{P} \subseteq \mathbf{P_{/poly}}\) and the Cook-Levin Theorem, as well as in Part IV (for \(\mathbf{BPP} \subseteq \mathbf{P_{/poly}}\) and derandomization) and Part V (specifically in cryptography and quantum computing).

  • All chapters in Part V (Advanced topics) are independent of one another and can be covered in any order.

A course based on this book can use all of Parts I, II, and III (possibly skipping over some or all of the \(\lambda\) calculus, Chapter 11, Chapter 10 or Chapter 17), and then either cover all or some of Part IV (randomized computation), and add a “sprinkling” of advanced topics from Part V based on student or instructor interest.

Exercises

Rank the significance of the following inventions in speeding up the multiplication of large (that is 100-digit or more) numbers. That is, use “back of the envelope” estimates to order them in terms of the speedup factor they offered over the previous state of affairs.

  1. Discovery of the grade-school digit by digit algorithm (improving upon repeated addition).

  2. Discovery of Karatsuba’s algorithm (improving upon the digit by digit algorithm).

  3. Invention of modern electronic computers (improving upon calculations with pen and paper).

The 1977 Apple II personal computer had a processor speed of 1.023 Mhz or about \(10^6\) operations per second. At the time of this writing the world’s fastest supercomputer performs 93 “petaflops” (\(10^{15}\) floating point operations per second) or about \(10^{18}\) basic steps per second. For each one of the following running times (as a function of the input length \(n\)), compute for both computers how large an input they could handle in a week of computation, if they run an algorithm that has this running time:

  1. \(n\) operations.

  2. \(n^2\) operations.

  3. \(n\log n\) operations.

  4. \(2^n\) operations.

  5. \(n!\) operations.

In this chapter we mentioned several companies that were founded based on the discovery of new algorithms. Can you give an example for a company that was founded based on the non-existence of an algorithm? See footnote for hint.4

  1. Suppose that \(T_1,T_2,T_3,\ldots\) is a sequence of numbers such that \(T_2 \leq 10\) and for every \(n\), \(T_n \leq 3T_{\lfloor n/2 \rfloor+1} + Cn\) for some \(C \geq 1\). Prove that \(T_n \leq 20Cn^{\log_2 3}\) for every \(n>2\).5

  2. Prove that the number of single-digit operations that Karatsuba’s algorithm takes to multiply two \(n\) digit numbers is at most \(1000n^{\log_2 3}\).

Implement in the programming language of your choice functions Gradeschool_multiply(x,y) and Karatsuba_multiply(x,y) that take two arrays of digits x and y and return an array representing the product of x and y (where x is identified with the number x[0]+10*x[1]+100*x[2]+... etc..) using the grade-school algorithm and the Karatsuba algorithm respectively. At what number of digits does the Karatsuba algorithm beat the grade-school one?

In this exercise, we show that if for some \(\omega>2\), we can write the product of two \(k\times k\) real-valued matrices \(A,B\) using at most \(k^\omega\) multiplications, then we can multiply two \(n\times n\) matrices in roughly \(n^\omega\) time for every large enough \(n\).

To make this precise, we need to make some notation that is unfortunately somewhat cumbersome. Assume that there is some \(k\in \N\) and \(m \leq k^\omega\) such that for every \(k\times k\) matrices \(A,B,C\) such that \(C=\ensuremath{\mathit{AB}}\), we can write for every \(i,j \in [k]\):

\[ C_{i,j} = \sum_{\ell=0}^{m-1} \alpha_{i,j}^\ell f_\ell(A)g_\ell(B) \]
for some linear functions \(f_0,\ldots,f_{m-1},g_0,\ldots,g_{m-1}:\mathbb{R}^{n^2} \rightarrow \mathbb{R}\) and coefficients \(\{ \alpha_{i,j}^\ell \}_{i,j \in [k],\ell \in [m]}\). Prove that under this assumption for every \(\epsilon>0\), if \(n\) is sufficiently large, then there is an algorithm that computes the product of two \(n\times n\) matrices using at most \(O(n^{\omega+\epsilon})\) arithmetic operations. See footnote for hint.6

Bibliographical notes

For a brief overview of what we’ll see in this book, you could do far worse than read Bernard Chazelle’s wonderful essay on the Algorithm as an Idiom of modern science. The book of Moore and Mertens (Moore, Mertens, 2011) gives a wonderful and comprehensive overview of the theory of computation, including much of the content discussed in this chapter and the rest of this book. Aaronson’s book (Aaronson, 2013) is another great read that touches upon many of the same themes.

For more on the algorithms the Babylonians used, see Knuth’s paper and Neugebauer’s classic book.

Many of the algorithms we mention in this chapter are covered in algorithms textbooks such as those by Cormen, Leiserson, Rivest, and Stein (Cormen, Leiserson, Rivest, Stein, 2009) , Kleinberg and Tardos (Kleinberg, Tardos, 2006) , and Dasgupta, Papadimitriou and Vazirani (Dasgupta, Papadimitriou, Vazirani, 2008) , as well as Jeff Erickson’s textbook. Erickson’s book is freely available online and contains a great exposition of recursive algorithms in general and Karatsuba’s algorithm in particular.

The story of Karatsuba’s discovery of his multiplication algorithm is recounted by him in (Karatsuba, 1995) . As mentioned above, further improvements were made by Toom and Cook (Toom, 1963) (Cook, 1966) , Schönhage and Strassen (Schönhage, Strassen, 1971) , Fürer (Fürer, 2007) , and recently by Harvey and Van Der Hoeven (Harvey, Van Der Hoeven, 2019) , see this article for a nice overview. The last papers crucially rely on the Fast Fourier transform algorithm. The fascinating story of the (re)discovery of this algorithm by John Tukey in the context of the cold war is recounted in (Cooley, 1987) . (We say re-discovery because it later turned out that the algorithm dates back to Gauss (Heideman, Johnson, Burrus, 1985) .) The Fast Fourier Transform is covered in some of the books mentioned below, and there are also online available lectures such as Jeff Erickson’s. See also this popular article by David Austin. Fast matrix multiplication was discovered by Strassen (Strassen, 1969) , and since then this has been an active area of research. (Bläser, 2013) is a recommended self-contained survey of this area.

The Backpropagation algorithm for fast differentiation of neural networks was invented by Werbos (Werbos, 1974) . The Pagerank algorithm was invented by Larry Page and Sergey Brin (Page, Brin, Motwani, Winograd, 1999) . It is closely related to the HITS algorithm of Kleinberg (Kleinberg, 1999) . The Akamai company was founded based on the consistent hashing data structure described in (Karger, Lehman, Leighton, Panigrahy, Levine, Lewin, 1997) . Compressed sensing has a long history but two foundational papers are (Candes, Romberg, Tao, 2006) (Donoho, 2006) . (Lustig, Donoho, Santos, Pauly, 2008) gives a survey of applications of compressed sensing to MRI; see also this popular article by Ellenberg (Ellenberg, 2010) . The deterministic polynomial-time algorithm for testing primality was given by Agrawal, Kayal, and Saxena (Agrawal, Kayal, Saxena, 2004) .

We alluded briefly to classical impossibility results in mathematics, including the impossibility of proving Euclid’s fifth postulate from the other four, impossibility of trisecting an angle with a straightedge and compass and the impossibility of solving a quintic equation via radicals. A geometric proof of the impossibility of angle trisection (one of the three geometric problems of antiquity, going back to the ancient Greeks) is given in this blog post of Tao. The book of Mario Livio (Livio, 2005) covers some of the background and ideas behind these impossibility results. Some exciting recent research is focused on trying to use computational complexity to shed light on fundamental questions in physics such as understanding black holes and reconciling general relativity with quantum mechanics

  1. This quote is typically read as disparaging the importance of actual physical computers in Computer Science, but note that telescopes are absolutely essential to astronomy as they provide us with the means to connect theoretical predictions with actual experimental observations.

    ↩

  2. To be fair, in the following sentence Graham says “you need to know how to calculate time and space complexity and about Turing completeness”. This book includes these topics, as well as others such as NP-hardness, randomization, cryptography, quantum computing, and more.

    ↩

  3. If \(x\) is a number then \(\floor{x}\) is the integer obtained by rounding it down, see Section 1.7.

    ↩

  4. As we will see in Chapter Chapter 21, almost any company relying on cryptography needs to assume the non-existence of certain algorithms. In particular, RSA Security was founded based on the security of the RSA cryptosystem, which presumes the non-existence of an efficient algorithm to compute the prime factorization of large integers.

    ↩

  5. Hint: Use a proof by induction - suppose that this is true for all \(n\)’s from \(1\) to \(m\) and prove that this is true also for \(m+1\).

    ↩

  6. Start by showing this for the case that \(n=k^t\) for some natural number \(t\), in which case you can do so recursively by breaking the matrices into \(k\times k\) blocks.

    ↩

Comments

Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.

Compiled on 12/06/2023 00:07:43

Copyright 2023, Boaz Barak. Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Produced using pandoc and panflute with templates derived from gitbook and bookdown.