Quantum computing

“We always have had (secret, secret, close the doors!) … a great deal of difficulty in understanding the world view that quantum mechanics represents … It has not yet become obvious to me that there’s no real problem. … Can I learn anything from asking this question about computers–about this may or may not be mystery as to what the world view of quantum mechanics is?” , Richard Feynman, 1981

“The only difference between a probabilistic classical world and the equations of the quantum world is that somehow or other it appears as if the probabilities would have to go negative”, Richard Feynman, 1981

There were two schools of natural philosophy in ancient Greece. Aristotle believed that objects have an essence that explains their behavior, and a theory of the natural world has to refer to the reasons (or “final cause” to use Aristotle’s language) as to why they exhibit certain phenomena. Democritus believed in a purely mechanistic explanation of the world. In his view, the universe was ultimately composed of elementary particles (or Atoms) and our observed phenomena arise from the interactions between these particles according to some local rules. Modern science (arguably starting with Newton) has embraced Democritus’ point of view, of a mechanistic or “clockwork” universe of particles and forces acting upon them.

While the classification of particles and forces evolved with time, to a large extent the “big picture” has not changed from Newton till Einstein. In particular it was held as an axiom that if we knew fully the current state of the universe (i.e., the particles and their properties such as location and velocity) then we could predict its future state at any point in time. In computational language, in all these theories the state of a system with \(n\) particles could be stored in an array of \(O(n)\) numbers, and predicting the evolution of the system can be done by running some efficient (e.g., \(poly(n)\) time) deterministic computation on this array.

The double slit experiment

Alas, in the beginning of the 20th century, several experimental results were calling into question this “clockwork” or “billiard ball” theory of the world. One such experiment is the famous double slit experiment. Here is one way to describe it. Suppose that we buy one of those baseball pitching machines, and aim it at a soft plastic wall, but put a metal barrier with a single slit between the machine and the plastic wall (see Figure 23.1). If we shoot baseballs at the plastic wall, then some of the baseballs would bounce off the metal barrier, while some would make it through the slit and dent the wall. If we now carve out an additional slit in the metal barrier then more balls would get through, and so the plastic wall would be even more dented.

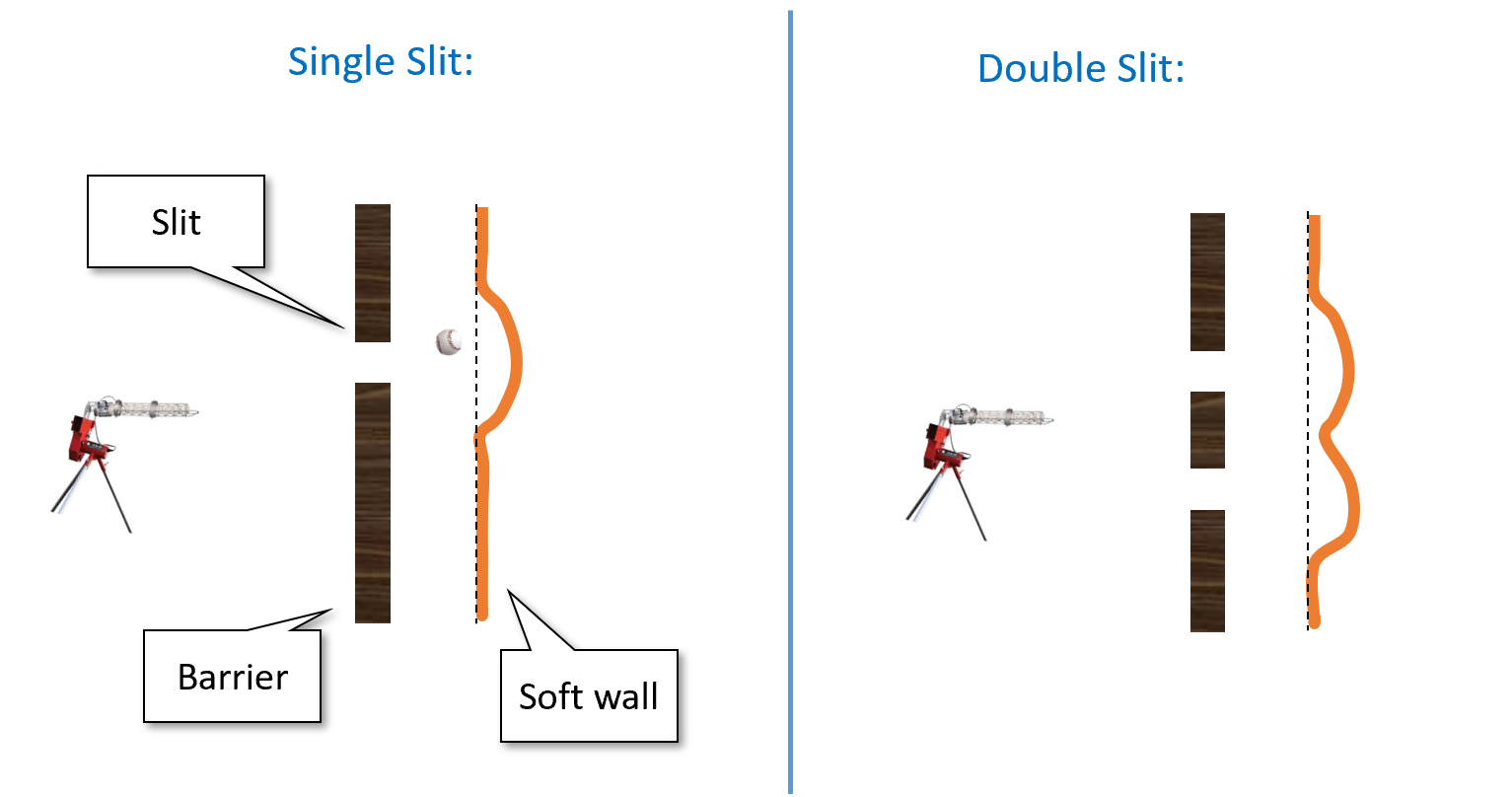
So far this is pure common sense, and it is indeed (to my knowledge) an accurate description of what happens when we shoot baseballs at a plastic wall. However, this is not the same when we shoot photons. Amazingly, if we shoot with a “photon gun” (i.e., a laser) at a wall equipped with photon detectors through some barrier, then (as shown in Figure 23.2) in some positions of the wall we will see fewer hits when the two slits are open than when only one of them is.¹ In particular there are positions in the wall that are hit when the first slit is open, hit when the second slit is open, but are not hit at all when both slits are open!

It seems as if each photon coming out of the gun is aware of the global setup of the experiment, and behaves differently if two slits are open than if only one is. If we try to “catch the photon in the act” and place a detector right next to each slit so we can see exactly the path each photon takes then something even more bizarre happens. The mere fact that we measure the path changes the photon’s behavior, and now this “destructive interference” pattern is gone and the number of times a position is hit when two slits are open is the sum of the number of times it is hit when each slit is open.

Quantum amplitudes

The double slit and other experiments ultimately forced scientists to accept a very counterintuitive picture of the world. It is not merely about nature being randomized, but rather it is about the probabilities in some sense “going negative” and cancelling each other!

To see what we mean by this, let us go back to the baseball experiment. Suppose that the probability a ball passes through the left slit is \(p_L\) and the probability that it passes through the right slit is \(p_R\). Then, if we shoot \(N\) balls out of each gun, we expect the wall will be hit \((p_L+p_R)N\) times. In contrast, in the quantum world of photons instead of baseballs, it can sometimes be the case that in both the first and second case the wall is hit with positive probabilities \(p_L\) and \(p_R\) respectively but somehow when both slits are open the wall (or a particular position in it) is not hit at all. It’s almost as if the probabilities can “cancel each other out”.

To understand the way we model this in quantum mechanics, it is helpful to think of a “lazy evaluation” approach to probability. We can think of a probabilistic experiment such as shooting a baseball through two slits in two different ways:

• When a ball is shot, “nature” tosses a coin and decides if it will go through the left slit (which happens with probability \(p_L\)), right slit (which happens with probability \(p_R\)), or bounce back. If it passes through one of the slits then it will hit the wall. Later we can look at the wall and find out whether or not this event happened, but the fact that the event happened or not is determined independently of whether or not we look at the wall.

• The other viewpoint is that when a ball is shot, “nature” computes the probabilities \(p_L\) and \(p_R\) as before, but does not yet “toss the coin” and determines what happened. Only when we actually look at the wall, nature tosses a coin and with probability \(p_L+p_R\) ensures we see a dent. That is, nature uses “lazy evaluation”, and only determines the result of a probabilistic experiment when we decide to measure it.

While the first scenario seems much more natural, the end result in both is the same (the wall is hit with probability \(p_L+p_R\)) and so the question of whether we should model nature as following the first scenario or second one seems like asking about the proverbial tree that falls in the forest with no one hearing it.

However, when we want to describe the double slit experiment with photons rather than baseballs, it is the second scenario that lends itself better to a quantum generalization. Quantum mechanics associates a number \(\alpha\) known as an amplitude with each probabilistic experiment. This number \(\alpha\) can be negative, and in fact even complex. We never observe the amplitudes directly, since whenever we measure an event with amplitude \(\alpha\), nature tosses a coin and determines that the event happens with probability \(|\alpha|^2\). However, the sign (or in the complex case, phase) of the amplitudes can affect whether two different events have constructive or destructive interference.

Specifically, consider an event that can either occur or not (e.g. “detector number 17 was hit by a photon”). In classical probability, we model this by a probability distribution over the two outcomes: a pair of non-negative numbers \(p\) and \(q\) such that \(p+q=1\), where \(p\) corresponds to the probability that the event occurs and \(q\) corresponds to the probability that the event does not occur. In quantum mechanics, we model this also by pair of numbers, which we call amplitudes. This is a pair of (potentially negative or even complex) numbers \(\alpha\) and \(\beta\) such that \(|\alpha|^2 + |\beta|^2 =1\). The probability that the event occurs is \(|\alpha|^2\) and the probability that it does not occur is \(|\beta|^2\). In isolation, these negative or complex numbers don’t matter much, since we square them anyway to obtain probabilities. But the interaction of positive and negative amplitudes can result in surprising cancellations where somehow combining two scenarios where an event happens with positive probability results in a scenario where it never does.

Quantum mechanics is a mathematical theory that allows us to calculate and predict the results of the double-slit and many other experiments. If you think of quantum mechanics as an explanation as to what “really” goes on in the world, it can be rather confusing. However, if you simply “shut up and calculate” then it works amazingly well at predicting experimental results. In particular, in the double slit experiment, for any position in the wall, we can compute numbers \(\alpha\) and \(\beta\) such that photons from the first and second slit hit that position with probabilities \(|\alpha|^2\) and \(|\beta|^2\) respectively. When we open both slits, the probability that the position will be hit is proportional to \(|\alpha+\beta|^2\), and so in particular, if \(\alpha=-\beta\) then it will be the case that, despite being hit when either slit one or slit two are open, the position is not hit at all when they both are. If you are confused by quantum mechanics, you are not alone: for decades people have been trying to come up with explanations for “the underlying reality” behind quantum mechanics, including Bohmian Mechanics, Many Worlds and others. However, none of these interpretations have gained universal acceptance and all of those (by design) yield the same experimental predictions. Thus at this point many scientists prefer to just ignore the question of what is the “true reality” and go back to simply “shutting up and calculating”.

Bell’s Inequality

There is something weird about quantum mechanics. In 1935 Einstein, Podolsky and Rosen (EPR) tried to pinpoint this issue by highlighting a previously unrealized corollary of this theory. They showed that the idea that nature does not determine the results of an experiment until it is measured results in so called “spooky action at a distance”. Namely, making a measurement of one object may instantaneously effect the state (i.e., the vector of amplitudes) of another object in the other end of the universe.

Since the vector of amplitudes is just a mathematical abstraction, the EPR paper was considered to be merely a thought experiment for philosophers to be concerned about, without bearing on experiments. This changed when in 1965 John Bell showed an actual experiment to test the predictions of EPR and hence pit intuitive common sense against the quantum mechanics. Quantum mechanics won: it turns out that it is in fact possible to use measurements to create correlations between the states of objects far removed from one another that cannot be explained by any prior theory. Nonetheless, since the results of these experiments are so obviously wrong to anyone that has ever sat in an armchair, that there are still a number of Bell denialists arguing that this can’t be true and quantum mechanics is wrong.

So, what is this Bell’s Inequality? Suppose that Alice and Bob try to convince you they have telepathic ability, and they aim to prove it via the following experiment. Alice and Bob will be in separate closed rooms.² You will interrogate Alice and your associate will interrogate Bob. You choose a random bit \(x\in\{0,1\}\) and your associate chooses a random \(y\in\{0,1\}\). We let \(a\) be Alice’s response and \(b\) be Bob’s response. We say that Alice and Bob win this experiment if \(a \oplus b = x \wedge y\). In other words, Alice and Bob need to output two bits that disagree if \(x=y=1\) and agree otherwise.³

Now if Alice and Bob are not telepathic, then they need to agree in advance on some strategy. It’s not hard for Alice and Bob to succeed with probability \(3/4\): just always output the same bit. Moreover, by doing some case analysis, we can show that no matter what strategy they use, Alice and Bob cannot succeed with higher probability than that:⁴

An amazing experimentally verified fact is that quantum mechanics allows for “telepathy”.⁵ Specifically, it has been shown that using the weirdness of quantum mechanics, there is in fact a strategy for Alice and Bob to succeed in this game with probability larger than \(3/4\) (in fact, they can succeed with probability about \(0.85\), see Lemma 23.5).

Quantum weirdness

Some of the counterintuitive properties that arise from quantum mechanics include:

• Interference - As we’ve seen, quantum amplitudes can “cancel each other out”.

• Measurement - The idea that amplitudes are negative as long as “no one is looking” and “collapse” (by squaring them) to positive probabilities when they are measured is deeply disturbing. Indeed, as shown by EPR and Bell, this leads to various strange outcomes such as “spooky actions at a distance”, where we can create correlations between the results of measurements in places far removed. Unfortunately (or fortunately?) these strange outcomes have been confirmed experimentally.

• Entanglement - The notion that two parts of the system could be connected in this weird way where measuring one will affect the other is known as quantum entanglement.

As counter-intuitive as these concepts are, they have been experimentally confirmed, so we just have to live with them.

Quantum computing and computation - an executive summary.

One of the strange aspects of the quantum-mechanical picture of the world is that unlike in the billiard ball example, there is no obvious algorithm to simulate the evolution of \(n\) particles over \(t\) time periods in \(poly(n,t)\) steps. In fact, the natural way to simulate \(n\) quantum particles will require a number of steps that is exponential in \(n\). This is a huge headache for scientists that actually need to do these calculations in practice.

In the 1981, physicist Richard Feynman proposed to “turn this lemon to lemonade” by making the following almost tautological observation:

If a physical system cannot be simulated by a computer in \(T\) steps, the system can be considered as performing a computation that would take more than \(T\) steps.

So, he asked whether one could design a quantum system such that its outcome \(y\) based on the initial condition \(x\) would be some function \(y=f(x)\) such that (a) we don’t know how to efficiently compute in any other way, and (b) is actually useful for something.⁶ In 1985, David Deutsch formally suggested the notion of a quantum Turing machine, and the model has been since refined in works of Deutsch and Josza and Bernstein and Vazirani. Such a system is now known as a quantum computer.

For a while these hypothetical quantum computers seemed useful for one of two things. First, to provide a general-purpose mechanism to simulate a variety of the real quantum systems that people care about, such as various interactions inside molecules in quantum chemistry. Second, as a challenge to the Extended Church Turing hypothesis which says that every physically realizable computation device can be modeled (up to polynomial overhead) by Turing machines (or equivalently, NAND-TM / NAND-RAM programs).

Quantum chemistry is important (and in particular understanding it can be a bottleneck for designing new materials, drugs, and more), but it is still a rather niche area within the broader context of computing (and even scientific computing) applications. Hence for a while most researchers (to the extent they were aware of it), thought of quantum computers as a theoretical curiosity that has little bearing to practice, given that this theoretical “extra power” of quantum computer seemed to offer little advantage in the majority of the problems people want to solve in areas such as combinatorial optimization, machine learning, data structures, etc..

To some extent this is still true today. As far as we know, quantum computers, if built, will not provide exponential speed ups for 95% of the applications of computing.⁷ In particular, as far as we know, quantum computers will not help us solve \(\mathbf{NP}\) complete problems in polynomial or even sub-exponential time, though Grover’s algorithm ( Remark 23.4) does yield a quadratic advantage in many cases.

However, there is one cryptography-sized exception: In 1994 Peter Shor showed that quantum computers can solve the integer factoring and discrete logarithm problems in polynomial time. This result has captured the imagination of a great many people, and completely energized research into quantum computing. This is both because the hardness of these particular problems provides the foundations for securing such a huge part of our communications (and these days, our economy), and because it was a powerful demonstration that quantum computers could turn out to be useful for problems that a-priori seem to have nothing to do with quantum physics.

As we’ll discuss later, at the moment there are several intensive efforts to construct large scale quantum computers. It seems safe to say that, as far as we know, in the next five years or so there will not be a quantum computer large enough to factor, say, a \(1024\) bit number. On the other hand, it does seem quite likely that in the very near future there will be quantum computers which achieve some task exponentially faster than the best-known way to achieve the same task with a classical computer. When and if a quantum computer is built that is strong enough to break reasonable parameters of Diffie Hellman, RSA and elliptic curve cryptography is anybody’s guess. It could also be a “self destroying prophecy” whereby the existence of a small-scale quantum computer would cause everyone to shift away to lattice-based crypto which in turn will diminish the motivation to invest the huge resources needed to build a large scale quantum computer.⁸

Quantum systems

Before we talk about quantum computing, let us recall how we physically realize “vanilla” or classical computing. We model a logical bit that can equal \(0\) or a \(1\) by some physical system that can be in one of two states. For example, it might be a wire with high or low voltage, charged or uncharged capacitor, or even (as we saw) a pipe with or without a flow of water, or the presence or absence of a soldier crab. A classical system of \(n\) bits is composed of \(n\) such “basic systems”, each of which can be in either a “zero” or “one” state. We can model the state of such a system by a string \(s \in \{0,1\}^n\). If we perform an operation such as writing to the 17-th bit the NAND of the 3rd and 5th bits, this corresponds to applying a local function to \(s\) such as setting \(s_{17} = 1 - s_3\cdot s_5\).

In the probabilistic setting, we would model the state of the system by a distribution. For an individual bit, we could model it by a pair of non-negative numbers \(\alpha,\beta\) such that \(\alpha+\beta=1\), where \(\alpha\) is the probability that the bit is zero and \(\beta\) is the probability that the bit is one. For example, applying the negation (i.e., NOT) operation to this bit corresponds to mapping the pair \((\alpha,\beta)\) to \((\beta,\alpha)\) since the probability that \(\ensuremath{\mathit{NOT}}(\sigma)\) is equal to \(1\) is the same as the probability that \(\sigma\) is equal to \(0\). This means that we can think of the NOT function as the linear map \(N:\R^2 \rightarrow \R^2\) such that \(N \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} \beta \\ \alpha \end{pmatrix}\) or equivalently as the matrix \(\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\).

If we think of the \(n\)-bit system as a whole, then since the \(n\) bits can take one of \(2^n\) possible values, we model the state of the system as a vector \(p\) of \(2^n\) probabilities. For every \(s\in \{0,1\}^n\), we denote by \(e_s\) the \(2^n\) dimensional vector that has \(1\) in the coordinate corresponding to \(s\) (identifying it with a number in \([2^n]\)), and so can write \(p\) as \(\sum_{s\in \{0,1\}^n} p_s e_s\) where \(p_s\) is the probability that the system is in the state \(s\).

Applying the operation above of setting the \(17\)-th bit to the NAND of the 3rd and 5th bits, corresponds to transforming the vector \(p\) to the vector \(Fp\) where \(F:\R^{2^n} \rightarrow \R^{2^n}\) is the linear map that maps \(e_s\) to \(e_{s_0\cdots s_{16}(1-s_3\cdot s_5)s_{18}\cdots s_{n-1}}\).⁹

Quantum amplitudes

In the quantum setting, the state of an individual bit (or “qubit”, to use quantum parlance) is modeled by a pair of numbers \((\alpha,\beta)\) such that \(|\alpha|^2 + |\beta|^2 = 1\). While in general these numbers can be complex, for the rest of this chapter, we will often assume they are real (though potentially negative), and hence often drop the absolute value operator. (This turns out not to make much of a difference in explanatory power.) As before, we think of \(\alpha^2\) as the probability that the bit equals \(0\) and \(\beta^2\) as the probability that the bit equals \(1\). As we did before, we can model the NOT operation by the map \(N:\R^2 \rightarrow \R^2\) where \(N(\alpha,\beta)=(\beta,\alpha)\).

Following quantum tradition, instead of using \(e_0\) and \(e_1\) as we did above, from now on we will denote the vector \((1,0)\) by \(|0\rangle\) and the vector \((0,1)\) by \(|1\rangle\) (and moreover, think of these as column vectors). This is known as the Dirac “ket” notation. This means that NOT is the unique linear map \(N:\R^2 \rightarrow \R^2\) that satisfies \(N |0\rangle=|1\rangle\) and \(N |1\rangle =|0\rangle\). In other words, in the quantum case, as in the probabilistic case, NOT corresponds to the matrix

In classical computation, we typically think that there are only two operations that we can do on a single bit: keep it the same or negate it. In the quantum setting, a single bit operation corresponds to any linear map \(\ensuremath{\mathit{OP}}:\R^2 \rightarrow \R^2\) that is norm preserving in the sense that for every \(\alpha,\beta\), if we apply \(\ensuremath{\mathit{OP}}\) to the vector \(\begin{pmatrix} \alpha \\ \beta \end{pmatrix}\) then we obtain a vector \(\begin{pmatrix} \alpha' \\ \beta' \end{pmatrix}\) such that \(\alpha'^2 + \beta'^2 = \alpha^2 + \beta^2\). Such a linear map \(\ensuremath{\mathit{OP}}\) corresponds to a unitary two by two matrix.¹⁰ Keeping the bit the same corresponds to the matrix \(I = \begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}\) and (as we’ve seen) the NOT operations corresponds to the matrix \(N = \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}\). But there are other operations we can use as well. One such useful operation is the Hadamard operation, which corresponds to the matrix

In fact it turns out that Hadamard is all that we need to add to a classical universal basis to achieve the full power of quantum computing.

Recap

The state of a quantum system of \(n\) qubits is modeled by an \(2^n\) dimensional vector \(\psi\) of unit norm (i.e., squares of all coordinates sums up to \(1\)), which we write as \(\psi=\sum_{x\in \{0,1\}^n} \psi_x |x \rangle\) where \(|x\rangle\) is the column vector that has \(0\) in all coordinates except the one corresponding to \(x\) (identifying \(\{0,1\}^n\) with the numbers \(\{0,\ldots,2^n-1\}\)). We use the convention that if \(a,b\) are strings of lengths \(k\) and \(\ell\) respectively then we can write the \(2^{k+\ell}\) dimensional vector with \(1\) in the \(ab\)-th coordinate and zero elsewhere not just as \(|ab\rangle\) but also as \(|a\rangle |b \rangle\). In particular, for every \(x\in \{0,1\}^n\), we can write the vector \(|x\rangle\) also as \(|x_0\rangle |x_1\rangle \cdots |x_{n-1} \rangle\). This notation satisfies certain nice distributive laws such as \(|a\rangle(|b\rangle + |b'\rangle)|c \rangle = |abc \rangle + |ab'c\rangle\).

A quantum operation on such a system is modeled by a \(2^n \times 2^n\) unitary matrix \(U\) (one that satisfies \(\ensuremath{\mathit{UU}}^\top = I\) where \(U^\top\) is the transpose operation, or conjugate transpose for complex matrices). If the system is in state \(\psi\) and we apply to it the operation \(U\), then the new state of the system is \(U\psi\).

When we measure an \(n\)-qubit system in a state \(\psi= \sum_{x\in \{0,1\}^n} \psi_x |x \rangle\), then we observe the value \(x\in \{0,1\}^n\) with probability \(|\psi_x|^2\). In this case, the system collapses to the state \(|x \rangle\).

Analysis of Bell’s Inequality (optional)

Now that we have the notation in place, we can show a strategy for Alice and Bob to display “quantum telepathy” in Bell’s Game. Recall that in the classical case, Alice and Bob can succeed in the “Bell Game” with probability at most \(3/4 = 0.75\). We now show that quantum mechanics allows them to succeed with probability at least \(0.8\).¹¹

Quantum computation

Recall that in the classical setting, we modeled computation as obtained by a sequence of basic operations. We had two types of computational models:

• Non uniform models of computation such as Boolean circuits and NAND-CIRC programs, where a finite function \(f:\{0,1\}^n \rightarrow \{0,1\}\) is computable in size \(T\) if it can be expressed as a combination of \(T\) basic operations (gates in a circuit or lines in a NAND-CIRC program)

• Uniform models of computation such as Turing machines and NAND-TM programs, where an infinite function \(F:\{0,1\}^* \rightarrow \{0,1\}\) is computable in time \(T(n)\) if there is a single algorithm that on input \(x\in \{0,1\}^n\) evaluates \(F(x)\) using at most \(T(n)\) basic steps.

When considering efficient computation, we defined the class \(\mathbf{P}\) to consist of all infinite functions \(F:\{0,1\}^* \rightarrow \{0,1\}\) that can be computed by a Turing machine or NAND-TM program in time \(p(n)\) for some polynomial \(p(\cdot)\). We defined the class \(\mathbf{P_{/poly}}\) to consists of all infinite functions \(F:\{0,1\}^* \rightarrow \{0,1\}\) such that for every \(n\), the restriction \(F_{\upharpoonright n}\) of \(F\) to \(\{0,1\}^n\) can be computed by a Boolean circuit or NAND-CIRC program of size at most \(p(n)\) for some polynomial \(p(\cdot)\).

We will do the same for quantum computation, focusing mostly on the non uniform setting of quantum circuits, since that is simpler, and already illustrates the important differences with classical computing.

Quantum circuits

A quantum circuit is analogous to a Boolean circuit, and can be described as a directed acyclic graph. One crucial difference that the out degree of every vertex in a quantum circuit is at most one. This is because we cannot “reuse” quantum states without measuring them (which collapses their “probabilities”). Therefore, we cannot use the same qubit as input for two different gates.¹³ Another more technical difference is that to express our operations as unitary matrices, we will need to make sure all our gates are reversible. This is not hard to ensure. For example, in the quantum context, instead of thinking of \(\ensuremath{\mathit{NAND}}\) as a (non reversible) map from \(\{0,1\}^2\) to \(\{0,1\}\), we will think of it as the reversible map on three qubits that maps \(a,b,c\) to \(a,b,c\oplus \ensuremath{\mathit{NAND}}(a,b)\) (i.e., flip the last bit if \(\ensuremath{\mathit{NAND}}\) of the first two bits is \(1\)). Equivalently, the NAND operation corresponds to the \(8\times 8\) unitary matrix \(U_{NAND}\) such that (identifying \(\{0,1\}^3\) with \([8]\)) for every \(a,b,c \in \{0,1\}\), if \(|abc\rangle\) is the basis element with \(1\) in the \(abc\)-th coordinate and zero elsewhere, then \(U_{NAND} |abc\rangle =|ab(c \oplus \ensuremath{\mathit{NAND}}(a,b))\rangle\).¹⁴ If we order the rows and columns as \(000,001,010,\ldots,111\), then \(U_{NAND}\) can be written as the following matrix:

If we have an \(n\) qubit system, then for \(i,j,k \in [n]\), we will denote by \(U_{NAND}^{i,j,k}\) as the \(2^n \times 2^n\) unitary matrix that corresponds to applying \(U_{NAND}\) to the \(i\)-th, \(j\)-th, and \(k\)-th bits, leaving the others intact. That is, for every \(v = \sum_{x\in \{0,1\}^n} v_x |x \rangle\), \(U_{NAND}^{i,j,k}v = \sum_{x\in \{0,1\}^n}v_x |x_0 \cdots x_{k-1}(x_k \oplus \ensuremath{\mathit{NAND}}(x_i,x_j))x_{k+1} \cdots x_{n-1} \rangle\).

As mentioned above, we will also use the Hadamard or \(\ensuremath{\mathit{HAD}}\) operation. A quantum circuit is obtained by applying a sequence of \(U_{NAND}\) and \(\ensuremath{\mathit{HAD}}\) gates, which correspond to the matrix

Another way to define \(H\) is that for \(b \in \{0,1\}\), \(H |b\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{1}{\sqrt{2}} (-1)^b |1\rangle\). We define \(\ensuremath{\mathit{HAD}}^i\) to be the \(2^n \times 2^n\) unitary matrix that applies \(\ensuremath{\mathit{HAD}}\) to the \(i\)-th qubit and leaves the others intact. Using the ket notation, we can write this as

\[ \ensuremath{\mathit{HAD}}^i \; \sum_{x\in \{0,1\}^n} v_x |x \rangle \;=\; \tfrac{1}{\sqrt{2}}\sum_{x\in \{0,1\}^n}|x_0 \cdots x_{i-1}\rangle \left(|0\rangle + (-1)^{x_i}|1\rangle\right)|x_i \cdots x_{n-1} \rangle \;. \]

A quantum circuit is obtained by composing these basic operations on some \(m\) qubits. If \(m \geq n\), we use a circuit to compute a function \(f:\{0,1\}^n \rightarrow \{0,1\}\):

• On input \(x\), we initialize the system to hold \(x_0,\ldots,x_{n-1}\) in the first \(n\) qubits, and initialize all remaining \(m-n\) qubits to zero.

• We execute each elementary operation one by one.

• At the end of the computation, we measure the system, and output the result of the last qubit (i.e. the qubit in location \(m-1\)).¹⁵

• We say that the circuit computes \(f\), if the probability that this output equals \(f(x)\) is at least \(2/3\). Note that this probability is obtained by summing up the squares of the amplitudes of all coordinates in the final state of the system corresponding to vectors \(|y \rangle\) where \(y_{m-1}=f(x)\).

Formally this is defined as follows:

Once we have the notion of quantum circuits, we can define the quantum analog of \(\mathbf{P_{/poly}}\) (i.e., define the class of functions computable by polynomial size quantum circuits) as follows:

QNAND-CIRC programs (optional)

Just like in the classical case, there is an equivalence between circuits and straightline programs, and so we can define the programming language QNAND that is the quantum analog of our NAND-CIRC programming language. To do so, we only add a single operation: HAD(foo) which applies the single-bit operation \(H\) to the variable foo. We also use the following interpretation to make NAND reversible: foo = NAND(bar,blah) means that we modify foo to be the XOR of its original value and the NAND of bar and blah. (In other words, apply the \(8\) by \(8\) unitary transformation \(U_{NAND}\) defined above to the three qubits corresponding to foo, bar and blah.) If foo is initialized to zero then this makes no difference.

If \(P\) is a QNAND-CIRC program with \(n\) input variables, \(\ell\) workspace variables, and \(m\) output variables, then running it on the input \(x\in \{0,1\}^n\) corresponds to setting up a system with \(n+m+\ell\) qubits and performing the following process:

1. We initialize the input variables X[\(0\)] \(\ldots\) X[\(n-1\)] to \(x_0,\ldots,x_{n-1}\) and all other variables to \(0\).

2. We execute the program line by line, applying the corresponding physical operation \(H\) or \(U_{NAND}\) to the qubits that are referred to by the line.

3. We measure the output variables Y[\(0\)], \(\ldots\), Y[\(m-1\)] and output the result (if there is more than one output then we measure more variables).

Uniform computation

Just as in the classical case, we can define uniform computational models. For example, we can define the QNAND-TM programming language to be QNAND augmented with loops and arrays just like NAND-TM is obtained from NAND. Using this we can define the class \(\mathbf{BQP}\) which is the uniform analog of \(\mathbf{BQP_{/poly}}\). Just as in the classical setting it holds that \(\mathbf{BPP} \subseteq \mathbf{P_{/poly}}\), in the quantum setting it can be shown that \(\mathbf{BQP} \subseteq \mathbf{BQP_{/poly}}\). Just like the classical case, we can also use Quantum Turing Machines instead of QNAND-TM to define \(\mathbf{BQP}\).

Yet another way to define \(\mathbf{BQP}\) is the following: a function \(F:\{0,1\}^* \rightarrow \{0,1\}\) is in \(\mathbf{BQP}\) if (1) \(F\in \mathbf{BQP_{/poly}}\) and (2) moreover for every \(n\), the quantum circuit that verifies this can be generated by a classical polynomial time NAND-TM program (or, equivalently, a polynomial-time Turing machine).¹⁶ We use this definition here, though an equivalent one can be made using QNAND-TM or quantum Turing machines:

The relation between \(\mathbf{NP}\) and \(\mathbf{BQP}\) is not known (see also Remark 23.4). It is widely believed that \(\mathbf{NP} \not\subseteq \mathbf{BQP}\), but there is no consensus whether or not \(\mathbf{BQP} \subseteq \mathbf{NP}\). It is quite possible that these two classes are incomparable, in the sense that \(\mathbf{NP} \nsubseteq \mathbf{BQP}\) (and in particular no \(\mathbf{NP}\)-complete function belongs to \(\mathbf{BQP}\)) but also \(\mathbf{BQP} \nsubseteq \mathbf{NP}\) (and there are some interesting candidates for such problems).

It can be shown that \(\ensuremath{\mathit{QNANDEVAL}}\) (evaluating a quantum circuit on an input) is computable by a polynomial size QNAND-CIRC program, and moreover this program can even be generated uniformly and hence \(\ensuremath{\mathit{QNANDEVAL}}\) is in \(\mathbf{BQP}\). This allows us to “port” many of the results of classical computational complexity into the quantum realm as well.

Physically realizing quantum computation

To realize quantum computation one needs to create a system with \(n\) independent binary states (i.e., “qubits”), and be able to manipulate small subsets of two or three of these qubits to change their state. While by the way we defined operations above it might seem that one needs to be able to perform arbitrary unitary operations on these two or three qubits, it turns out that there several choices for universal sets - a small constant number of gates that generate all others. The biggest challenge is how to keep the system from being measured and collapsing to a single classical combination of states. This is sometimes known as the coherence time of the system. The threshold theorem says that there is some absolute constant level of errors \(\tau\) so that if errors are created at every gate at rate smaller than \(\tau\) then we can recover from those and perform arbitrary long computations. (Of course there are different ways to model the errors and so there are actually several threshold theorems corresponding to various noise models).

There have been several proposals to build quantum computers:

• Superconducting quantum computers use super-conducting electric circuits to do quantum computation. These are currently the devices with largest number of fully controllable qubits.

• At Harvard, Lukin’s group is using cold atoms to implement quantum computers.

• Trapped ion quantum computers use the states of an ion to simulate a qubit. People have made some recent advances on these computers too. For example, an ion-trap computer was used to implement Shor’s algorithm to factor 15. (It turns out that \(15=3\times 5\) :) )

• Topological quantum computers use a different technology, which is more stable by design but arguably harder to manipulate to create quantum computers.

These approaches are not mutually exclusive and it could be that ultimately quantum computers are built by combining all of them together. At the moment, we have devices with about \(100\) qubits, and about \(1\%\) error per gate. Such restricted machines are sometimes called “Noisy Intermediate-Scale Quantum Computers” or “NISQ”. See this article by John Preskil for some of the progress and applications of such more restricted devices. If the number of qubits is increased and the error is decreased by one or two orders of magnitude, we could start seeing more applications.

Shor’s Algorithm: Hearing the shape of prime factors

Bell’s Inequality is a powerful demonstration that there is something very strange going on with quantum mechanics. But could this “strangeness” be of any use to solve computational problems not directly related to quantum systems? A priori, one could guess the answer is no. In 1994 Peter Shor showed that one would be wrong:

Another way to state Theorem 23.12 is that if we define \(\ensuremath{\mathit{FACTORING}}:\{0,1\}^* \rightarrow \{0,1\}\) to be the function that on input a pair of numbers \((M,X)\) outputs \(1\) if and only if \(M\) has a factor \(P\) such that \(2 \leq P \leq X\), then \(\ensuremath{\mathit{FACTORING}}\) is in \(\mathbf{BQP}\). This is an exponential improvement over the best known classical algorithms, which take roughly \(2^{\tilde{O}(n^{1/3})}\) time, where the \(\tilde{O}\) notation hides factors that are polylogarithmic in \(n\). While we will not prove Theorem 23.12 in this chapter, we will sketch some of the ideas behind the proof.

Period finding

At the heart of Shor’s Theorem is an efficient quantum algorithm for finding periods of a given function. For example, a function \(f:\R \rightarrow \R\) is periodic if there is some \(h>0\) such that \(f(x+h)=f(x)\) for every \(x\) (e.g., see Figure 23.4).

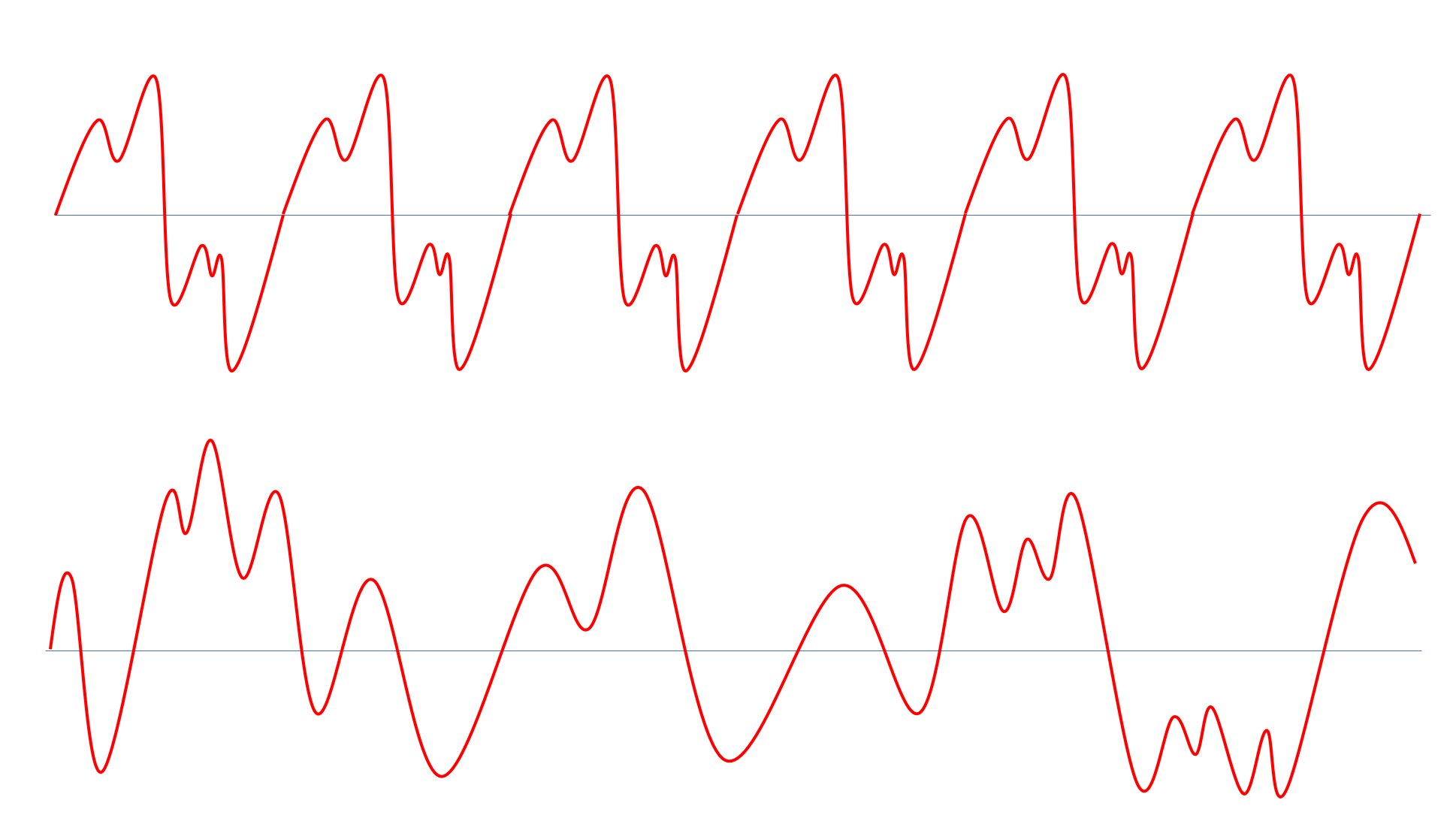
Musical notes yield one type of periodic function. When you pull on a string on a musical instrument, it vibrates in a repeating pattern. Hence, if we plot the speed of the string (and so also the speed of the air around it) as a function of time, it will correspond to some periodic function. The length of the period is known as the wave length of the note. The frequency is the number of times the function repeats itself within a unit of time. For example, the “Middle C” note has a frequency of \(261.63\) Hertz, which means its period is \(1/(261.63)\) seconds.

If we play a chord by playing several notes at once, we get a more complex periodic function obtained by combining the functions of the individual notes (see Figure 23.5). The human ear contains many small hairs, each of which is sensitive to a narrow band of frequencies. Hence when we hear the sound corresponding to a chord, the hairs in our ears actually separate it out to the components corresponding to each frequency.

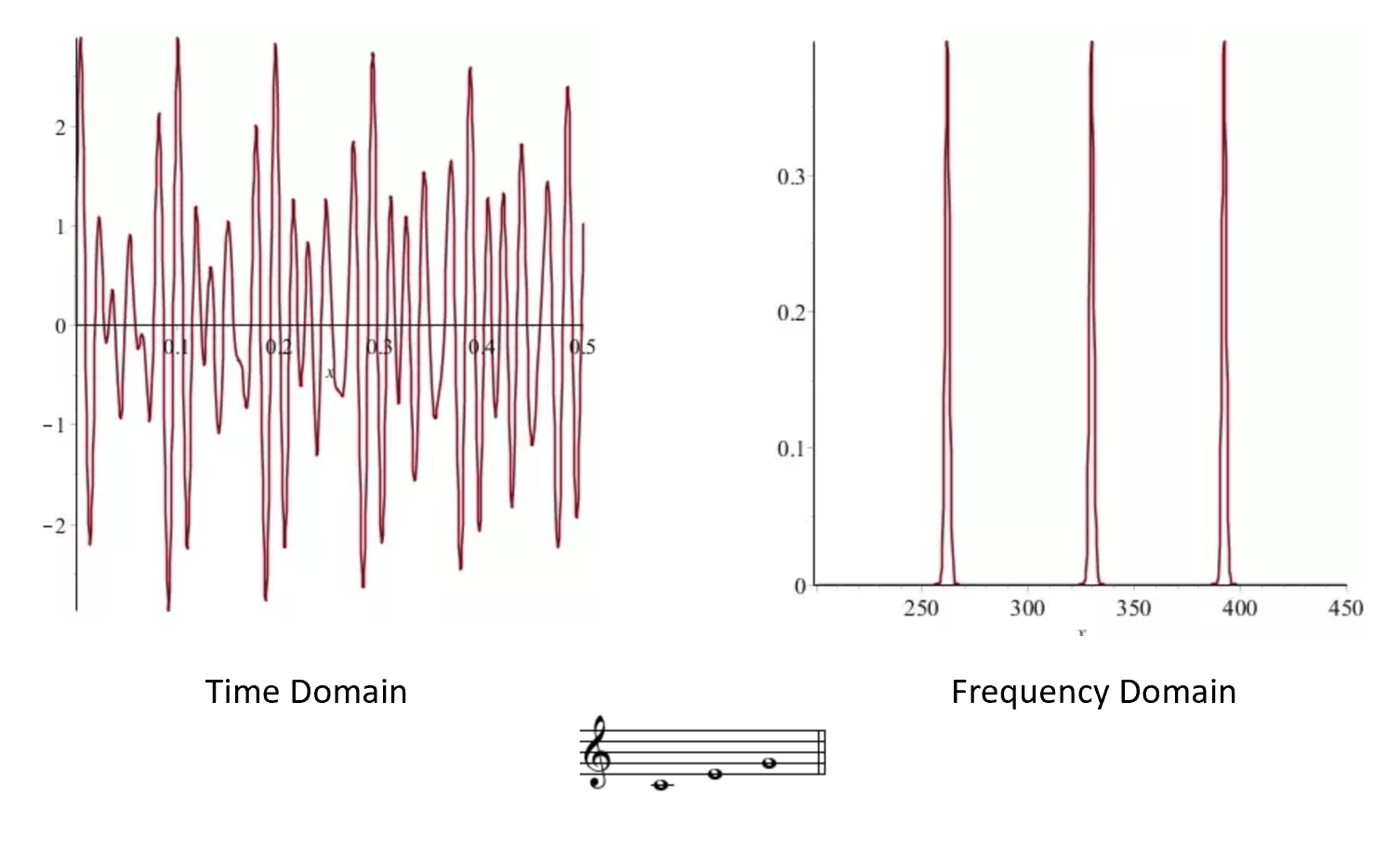
It turns out that (essentially) every periodic function \(f:\R \rightarrow \R\) can be decomposed into a sum of simple wave functions (namely functions of the form \(x \mapsto \sin(\theta x)\) or \(x \mapsto \cos(\theta x)\)). This is known as the Fourier Transform (see Figure 23.6). The Fourier transform makes it easy to compute the period of a given function: it will simply be the least common multiple of the periods of the constituent waves.

Shor’s Algorithm: A bird’s eye view

On input a an integer \(M\), Shor’s algorithm outputs the prime factorization of \(M\) in time that is polynomial in \(\log M\). The main steps in the algorithm are the following:

Step 1: Reduce to period finding. The first step in the algorithm is to pick a random \(A\in \{0,1\ldots,M-1\}\) and define the function \(F_A:\{0,1\}^m \rightarrow \{0,1\}^m\) as \(F_A(x)= A^x (\mod M)\) where we identify the string \(x \in \{0,1\}^m\) with an integer using the binary representation, and similarly represent the integer \(A^x (\mod M)\) as a string. (We will choose \(m\) to be some polynomial in \(m\) and so in particular \(\{0,1\}^m\) is a large enough set to represent all the numbers in \(\{0,1,\ldots, M-1 \}\)).

Some not-too-hard (though somewhat technical) calculations show that: (1) The function \(F_A\) is periodic (i.e., there is some integer \(p_A\) such that \(F_A(x+p_A)=F_A(x)\) for almost¹⁷ every \(x\)) and more importantly (2) If we can recover the period \(p_A\) of \(F_A\) for several randomly chosen \(A\)’s, then we can recover the factorization of \(M\). Hence, factoring \(M\) reduces to finding out the period of the function \(F_A\). Exercise 23.2 asks you to work out this for the related task of computing the discrete logarithm (which underlies the security of the Diffie-Hellman key exchange and elliptic curve cryptography).

Step 2: Period finding via the Quantum Fourier Transform. Using a simple trick known as “repeated squaring”, it is possible to compute the map \(x \mapsto F_A(x)\) in time polynomial in \(m\), which means we can also compute this map using a polynomial number of NAND gates,and so in particular we can generate in polynomial quantum time a quantum state \(\rho\) that is (up to normalization) equal to

In particular, if we were to measure the state \(\rho\), we would get a random pair of the form \((x,y)\) where \(y= F_A(x)\). So far, this is not at all impressive. After all, we did not need the power of quantum computing to generate such pairs: we could simply generate a random \(x\) and then compute \(F_A(x)\).

Another way to describe the state \(\rho\) is that the coefficient of \(|x \rangle |y \rangle\) in \(\rho\) is proportional to \(f_{A,y}(x)\) where \(f_{A,y} : \{0,1\}^m \rightarrow \R\) is the function such that

The magic of Shor’s algorithm comes from a procedure known as the Quantum Fourier Transform. It allows to change the state \(\rho\) into the state \(\hat{\rho}\) where the coefficient of \(|x\rangle|y \rangle\) is now proportional to the \(x\)-th Fourier coefficient of \(f_{A,y}\). In other words, if we measure the state \(\hat{\rho}\), we will obtain a pair \((x,y)\) such that the probability of choosing \(x\) is proportional to the square of the weight of the frequency \(x\) in the representation of the function \(f_{A,y}\). Since for every \(y\), the function \(f_{A,y}\) has the period \(p_A\), it can be shown that the frequency \(x\) will be (almost¹⁸) a multiple of \(p_A\). If we make several such samples \(y_0,\ldots,y_k\) and obtain the frequencies \(x_1,\ldots,x_k\), then the true period \(p_A\) divides all of them, and it can be shown that it is going to be in fact the greatest common divisor (g.c.d.) of all these frequencies: a value which can be computed in polynomial time.

As mentioned above, we can recover the factorization of \(M\) from the periods of \(F_{A_0},\ldots,F_{A_t}\) for some randomly chosen \(A_0,\ldots,A_t\) in \(\{0,\ldots, M-1\}\) and \(t\) which is polynomial in \(\log M\).

The resulting algorithm can be described in a high (and somewhat inaccurate) level as follows:

Shor’s Algorithm: (sketch)

Input: Number \(M\in \N\).

Output: Prime factorization of \(M\).

Operations:

1. Repeat the following \(k=poly(\log M)\) number of times:

   1. Choose \(A \in \{0,\ldots,M-1\}\) at random, and let \(f_A:\Z_M \rightarrow \Z_M\) be the map \(x \mapsto A^x \mod M\).

   2. For \(t=poly(\log M)\), repeat \(t\) times the following step: Quantum Fourier Transform to create a quantum state \(| \psi \rangle\) over \(poly(\log(m))\) qubits, such that if we measure \(| \psi \rangle\) we obtain a pair of strings \((j,y)\) with probability proportional to the square of the coefficient corresponding to the wave function \(x \mapsto \cos(x \pi j/M)\) or \(x \mapsto \sin(x \pi j/M)\) in the Fourier transform of the function \(f_{A,y}:\Z_m \rightarrow \{0,1\}\) defined as \(f_{A,y}(x)=1\) iff \(f_A(x)=y\).

   3. If \(j_1,\ldots,j_t\) are the coefficients we obtained in the previous step, then the least common multiple of \(M/j_1,\ldots,M/j_t\) is likely to be the period of the function \(f_A\).

2. If we let \(A_0,\ldots,A_{k-1}\) and \(p_0,\ldots,p_{k-1}\) be the numbers we chose in the previous step and the corresponding periods of the functions \(f_{A_0},\ldots,f_{A_{k-1}}\) then we can use classical results in number theory to obtain from these a non-trivial prime factor \(Q\) of \(M\) (if such exists). We can now run the algorithm again with the (smaller) input \(M/Q\) to obtain all other factors.

Reducing factoring to order finding is cummbersome, but can be done in polynomial time using a classical computer. The key quantum ingredient in Shor’s algorithm is the quantum fourier transform.

Quantum Fourier Transform (advanced, optional)

The above description of Shor’s algorithm skipped over the implementation of the main quantum ingredient: the Quantum Fourier Transform algorithm. In this section we discuss the ideas behind this algorithm. We will be rather brief and imprecise. Remark 23.3 and Section 23.13 contain references to sources of more information about this topic.

To understand the Quantum Fourier Transform, we need to better understand the Fourier Transform itself. In particular, we will need to understand how it applies not just to functions whose input is a real number but to functions whose domain can be any arbitrary commutative group. Therefore we now take a short detour to (very basic) group theory, and define the notion of periodic functions over groups.

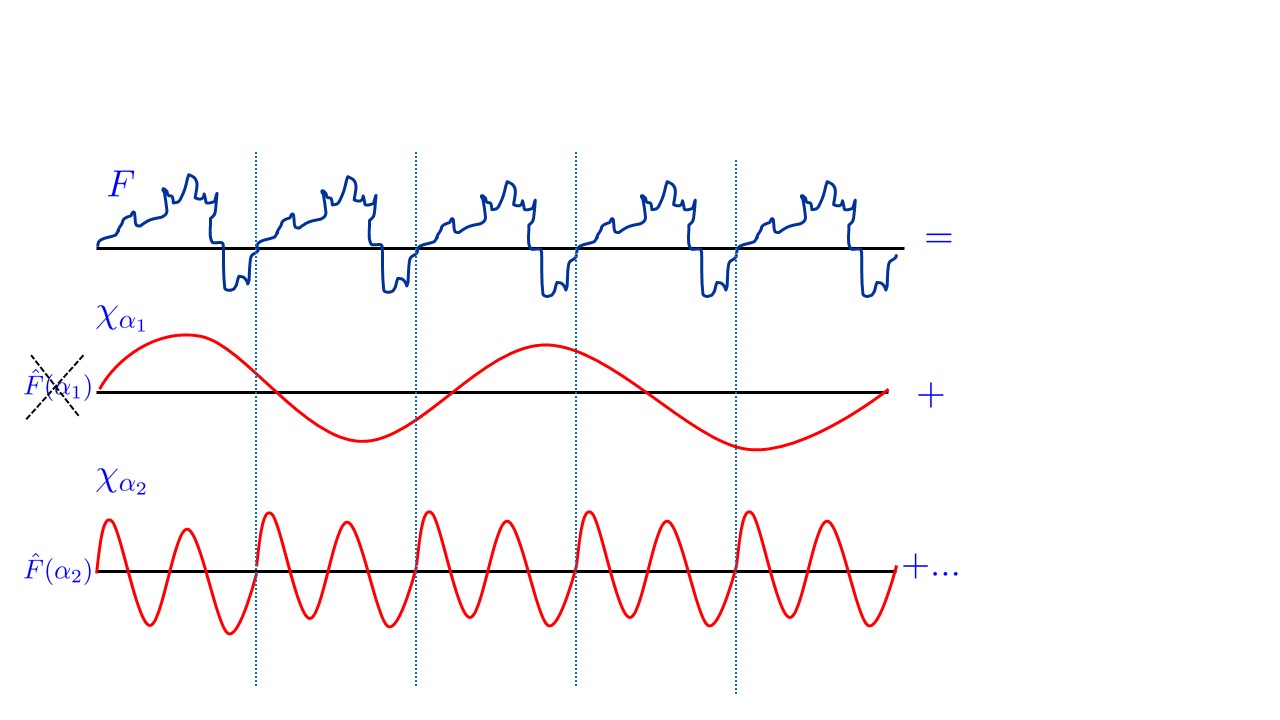
The Fourier transform is a deep and vast topic, on which we will barely touch upon here. Over the real numbers, the Fourier transform of a function \(f\) is obtained by expressing \(f\) in the form \(\sum \hat{f}(\alpha)\chi_\alpha\) where the \(\chi_\alpha\)’s are “wave functions” (e.g. sines and cosines). However, it turns out that the same notion exists for every Abelian group \(\mathbb{G}\). Specifically, for every such group \(\mathbb{G}\), if \(f\) is a function mapping \(\mathbb{G}\) to \(\mathbb{C}\), then we can write \(f\) as

where the \(\chi_g\)’s are functions mapping \(\mathbb{G}\) to \(\mathbb{C}\) that are analogs of the “wave functions” for the group \(\mathbb{G}\) and for every \(g\in \mathbb{G}\), \(\hat{f}(g)\) is a complex number known as the Fourier coefficient of \(f\) corresponding to \(g\).¹⁹ The representation Equation 23.2 is known as the Fourier expansion or Fourier transform of \(f\), the numbers \(( \hat{f}(g) )_{g\in\mathbb{G}}\) are known as the Fourier coefficients of \(f\) and the functions \(( \chi_g )_{g\in\mathbb{G}}\) are known as the Fourier characters. The central property of the Fourier characters is that they are homomorphisms of the group into the complex numbers, in the sense that for every \(x,x' \in \mathbb{G}\), \(\chi_g(x \star x')=\chi_g(x)\chi_g(x')\), where \(\star\) is the group operation. One corollary of this property is that if \(\chi_g(h)=1\) then \(\chi_g\) is \(h\) periodic in the sense that \(\chi_g(x \star h)=\chi_g(x)\) for every \(x\). It turns out that if \(f\) is periodic with minimal period \(h\), then the only Fourier characters that have non zero coefficients in the expression Equation 23.2 are those that are \(h\) periodic as well. This can be used to recover the period of \(f\) from its Fourier expansion.

Quantum Fourier Transform over the Boolean Cube: Simon’s Algorithm

We now describe the simplest setting of the Quantum Fourier Transform: the group \(\{0,1\}^n\) with the XOR operation, which we’ll denote by \((\{0,1\}^n,\oplus)\). It can be shown that the Fourier transform over \((\{0,1\}^n,\oplus)\) corresponds to expressing \(f:\{0,1\}^n \rightarrow \mathbb{C}\) as

where \(\chi_y:\{0,1\}^n \rightarrow \mathbb{C}\) is defined as \(\chi_y(x) = (-1)^{\sum_i y_i x_i}\) and \(\hat{f}(y) = \tfrac{1}{\sqrt{2^n}}\sum_{x\in \{0,1\}^n} f(x)(-1)^{\sum_i y_i x_i}\).

The Quantum Fourier Transform over \((\{0,1\}^n,\oplus)\) is actually qutie simple:

From Fourier to Period finding: Simon’s Algorithm (advanced, optional)

Using Theorem 23.15 it is not hard to get an algorithm that can recover a string \(h^* \in \{0,1\}^n\) given a circuit that computes a function \(F:\{0,1\}^n \rightarrow \{0,1\}^*\) that is \(h^*\) periodic in the sense that \(F(x)=F(x')\) for distinct \(x,x'\) if and only if \(x' = x \oplus h^*\). The key observation is that if we compute the state \(\sum_{x\in \{0,1\}^n} |x \rangle |F(x) \rangle\), and perform the Quantum Fourier transform on the first \(n\) qubits, then we would get a state such that the only basis elements with nonzero coefficients would be of the form \(|y \rangle\) where

So, by measuring the state, we can obtain a sample of a random \(y\) satisfying Equation 23.3. But since Equation 23.3 is a linear equation modulo \(2\) about the unknown \(n\) variables \(h^*_0,\ldots,h^*_{n-1}\), if we repeat this procedure to get \(n\) such equations, we will have at least as many equations as variables and (it can be shown that) this will suffice to recover \(h^*\).

This result is known as Simon’s Algorithm, and it preceded and inspired Shor’s algorithm.

From Simon to Shor (advanced, optional)

Theorem 23.15 seemed to really use the special bit-wise structure of the group \(\{0,1\}^n\), and so one could wonder if it can be extended to other groups. However, it turns out that we can in fact achieve such a generalization.

The key step in Shor’s algorithm is to implement the Fourier transform for the group \(\Z_L\) which is the set of numbers \(\{0,\ldots,L-1\}\) with the operation being addition modulo \(L\). In this case it turns out that the Fourier characters are the functions \(\chi_y(x) = \omega^{yx}\) where \(\omega = e^{2\pi i/L}\) (\(i\) here denotes the complex number \(\sqrt{-1}\)). The \(y\)-th Fourier coefficient of a function \(f:\Z_L \rightarrow \mathbb{C}\) is

The key to implementing the Quantum Fourier Transform for such groups is to use the same recursive equations that enable the classical Fast Fourier Transform (FFT) algorithm. Specifically, consider the case that \(L=2^\ell\). We can separate the sum over \(x\) in Equation 23.4 to the terms corresponding to even \(x\)’s (of the form \(x=2z\)) and odd \(x\)’s (of the form \(x=2z+1\)) to obtain

which reduces computing the Fourier transform of \(f\) over the group \(\Z_{2^\ell}\) to computing the Fourier transform of the functions \(f_{even}\) and \(f_{odd}\) (corresponding to the applying \(f\) to only the even and odd \(x\)’s respectively) which have \(2^{\ell-1}\) inputs that we can identify with the group \(\Z_{2^{\ell-1}}=\Z_{L/2}\).

Specifically, the Fourier characters of the group \(\Z_{L/2}\) are the functions \(\chi_y(x) = e^{2\pi i/(L/2) yx} = (\omega^2)^{yx}\) for every \(x,y \in \Z_{L/2}\). Moreover, since \(\omega^L = 1\), \((\omega^2)^y = (\omega^2)^{y \mod L/2}\) for every \(y\in \N\). Thus Equation 23.5 translates into

This observation is usually used to obtain a fast (e.g. \(O(L \log L)\)) time to compute the Fourier transform in a classical setting, but it can be used to obtain a quantum circuit of \(poly(\log L)\) gates to transform a state of the form \(\sum_{x\in \Z_L} f(x)|x\rangle\) to a state of the form \(\sum_{y\in \Z_L} \hat{f}(y)|y \rangle\).

The case that \(L\) is not an exact power of two causes some complications in both the classical case of the Fast Fourier Transform and the quantum setting of Shor’s algorithm. However, it is possible to handle these. The idea is that we can embed \(Z_L\) in the group \(\Z_{A\cdot L}\) for any integer \(A\), and we can find an integer \(A\) such that \(A\cdot L\) will be close enough to a power of \(2\) (i.e., a number of the form \(2^m\) for some \(m\)), so that if we do the Fourier transform over the group \(\Z_{2^m}\) then we will not introduce too many errors.

Exercises

Bibliographical notes

Chapters 9 and 10 in the book Quantum Computing Since Democritus give an informal but highly informative introduction to the topics of this lecture and much more. Shor’s and Simon’s algorithms are also covered in Chapter 10 of my book with Arora on computational complexity.

There are many excellent videos available online covering some of these materials. The Fourier transform is covered in this videos of Dr. Chris Geoscience, Clare Zhang and Vi Hart. More specifically to quantum computing, the videos of Umesh Vazirani on the Quantum Fourier Transform and Kelsey Houston-Edwards on Shor’s Algorithm are very recommended.

Chapter 10 in Avi Wigderson’s book gives a high level overview of quantum computing. Andrew Childs’ lecture notes on quantum algorithms, as well as the lecture notes of Umesh Vazirani, John Preskill, and John Watrous

Regarding quantum mechanics in general, this video illustrates the double slit experiment, this Scientific American video is a nice exposition of Bell’s Theorem. This talk and panel moderated by Brian Greene discusses some of the philosophical and technical issues around quantum mechanics and its so called “measurement problem”. The Feynmann lecture on the Fourier Transform and quantum mechanics in general are very much worth reading.

The Fast Fourier Transform, used as a component in Shor’s algorithm, is one of the most useful algorithms across many applications areas. The stories of its discovery by Gauss in trying to calculate asteroid orbits and rediscovery by Tukey during the cold war are fascinating as well.

Further explorations

Some topics related to this chapter that might be accessible to advanced students include: (to be completed)

Acknowledgements

Thanks to Scott Aaronson for many helpful comments about this chapter.

Comments

Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.

Compiled on 12/06/2023 00:07:20

Copyright 2023, Boaz Barak.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Produced using pandoc and panflute with templates derived from gitbook and bookdown.