See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
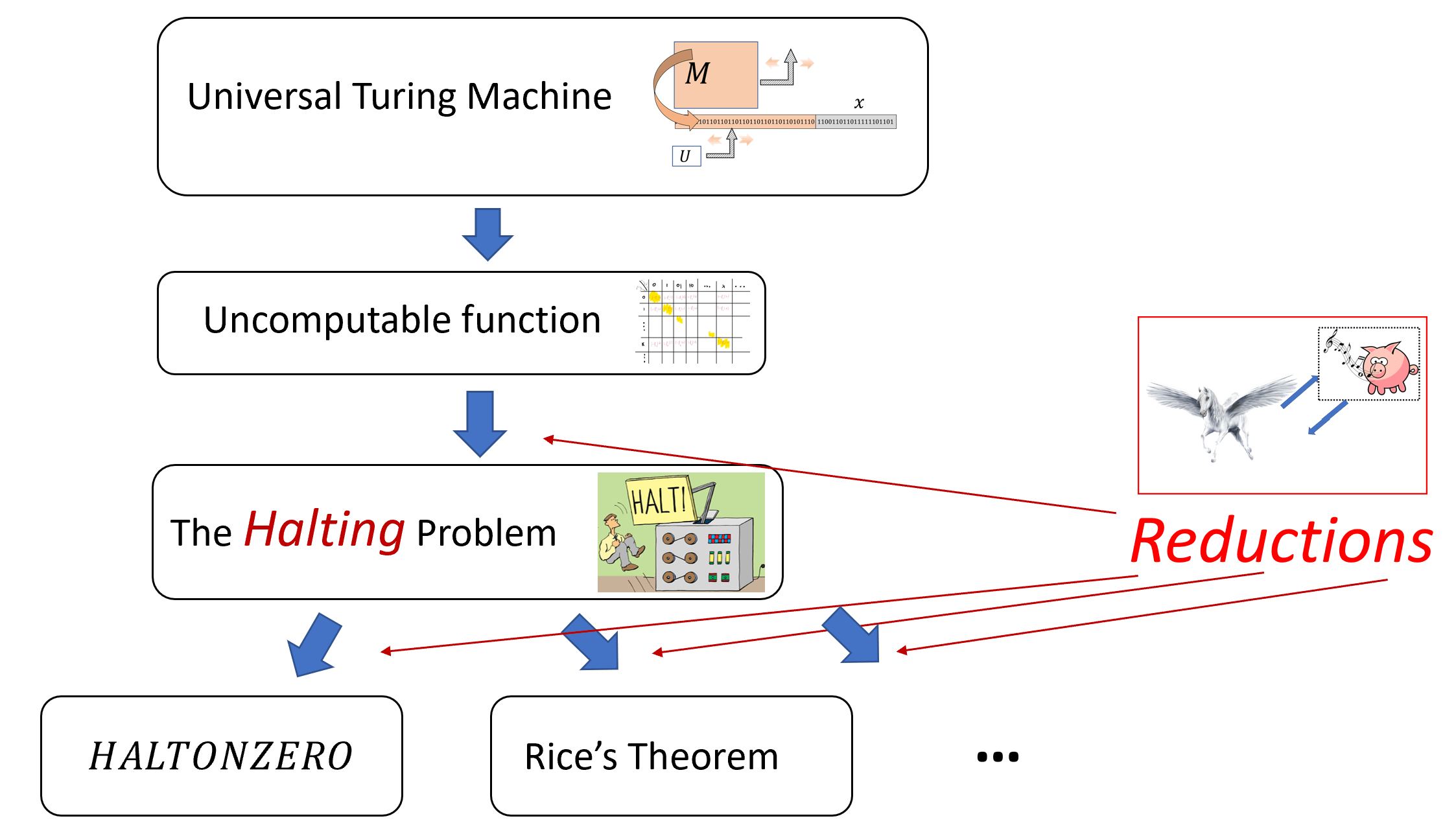
Universality and uncomputability
- The universal machine/program - “one program to rule them all”
- A fundamental result in computer science and mathematics: the existence of uncomputable functions.
- The halting problem: the canonical example of an uncomputable function.
- Introduction to the technique of reductions.
- Rice’s Theorem: A “meta tool” for uncomputability results, and a starting point for much of the research on compilers, programming languages, and software verification.
“A function of a variable quantity is an analytic expression composed in any way whatsoever of the variable quantity and numbers or constant quantities.”, Leonhard Euler, 1748.
“The importance of the universal machine is clear. We do not need to have an infinity of different machines doing different jobs. … The engineering problem of producing various machines for various jobs is replaced by the office work of ‘programming’ the universal machine”, Alan Turing, 1948
One of the most significant results we showed for Boolean circuits (or equivalently, straight-line programs) is the notion of universality: there is a single circuit that can evaluate all other circuits. However, this result came with a significant caveat. To evaluate a circuit of \(s\) gates, the universal circuit needed to use a number of gates larger than \(s\). It turns out that uniform models such as Turing machines or NAND-TM programs allow us to “break out of this cycle” and obtain a truly universal Turing machine \(U\) that can evaluate all other machines, including machines that are more complex (e.g., more states) than \(U\) itself. (Similarly, there is a Universal NAND-TM program \(U'\) that can evaluate all NAND-TM programs, including programs that have more lines than \(U'\).)
It is no exaggeration to say that the existence of such a universal program/machine underlies the information technology revolution that began in the latter half of the 20th century (and is still ongoing). Up to that point in history, people have produced various special-purpose calculating devices such as the abacus, the slide ruler, and machines that compute various trigonometric series. But as Turing (who was perhaps the one to see most clearly the ramifications of universality) observed, a general purpose computer is much more powerful. Once we build a device that can compute the single universal function, we have the ability, via software, to extend it to do arbitrary computations. For example, if we want to simulate a new Turing machine \(M\), we do not need to build a new physical machine, but rather can represent \(M\) as a string (i.e., using code) and then input \(M\) to the universal machine \(U\).
Beyond the practical applications, the existence of a universal algorithm also has surprising theoretical ramifications, and in particular can be used to show the existence of uncomputable functions, upending the intuitions of mathematicians over the centuries from Euler to Hilbert. In this chapter we will prove the existence of the universal program, and also show its implications for uncomputability, see Figure 9.1
In this chapter we will see two of the most important results in Computer Science:
The existence of a universal Turing machine: a single algorithm that can evaluate all other algorithms,
The existence of uncomputable functions: functions (including the famous “Halting problem”) that cannot be computed by any algorithm.
Along the way, we develop the technique of reductions as a way to show hardness of computing a function. A reduction gives a way to compute a certain function using “wishful thinking” and assuming that another function can be computed. Reductions are of course widely used in programming - we often obtain an algorithm for one task by using another task as a “black box” subroutine. However we will use it in the “contra positive”: rather than using a reduction to show that the former task is “easy”, we use them to show that the latter task is “hard”. Don’t worry if you find this confusing - reductions are initially confusing - but they can be mastered with time and practice.
Universality or a meta-circular evaluator
We start by proving the existence of a universal Turing machine. This is a single Turing machine \(U\) that can evaluate arbitrary Turing machines \(M\) on arbitrary inputs \(x\), including machines \(M\) that can have more states and larger alphabet than \(U\) itself. In particular, \(U\) can even be used to evaluate itself! This notion of self reference will appear time and again in this book, and as we will see, leads to several counter-intuitive phenomena in computing.
There exists a Turing machine \(U\) such that on every string \(M\) which represents a Turing machine, and \(x\in \{0,1\}^*\), \(U(M,x)=M(x)\).
That is, if the machine \(M\) halts on \(x\) and outputs some \(y\in \{0,1\}^*\) then \(U(M,x)=y\), and if \(M\) does not halt on \(x\) (i.e., \(M(x)=\bot\)) then \(U(M,x)=\bot\).
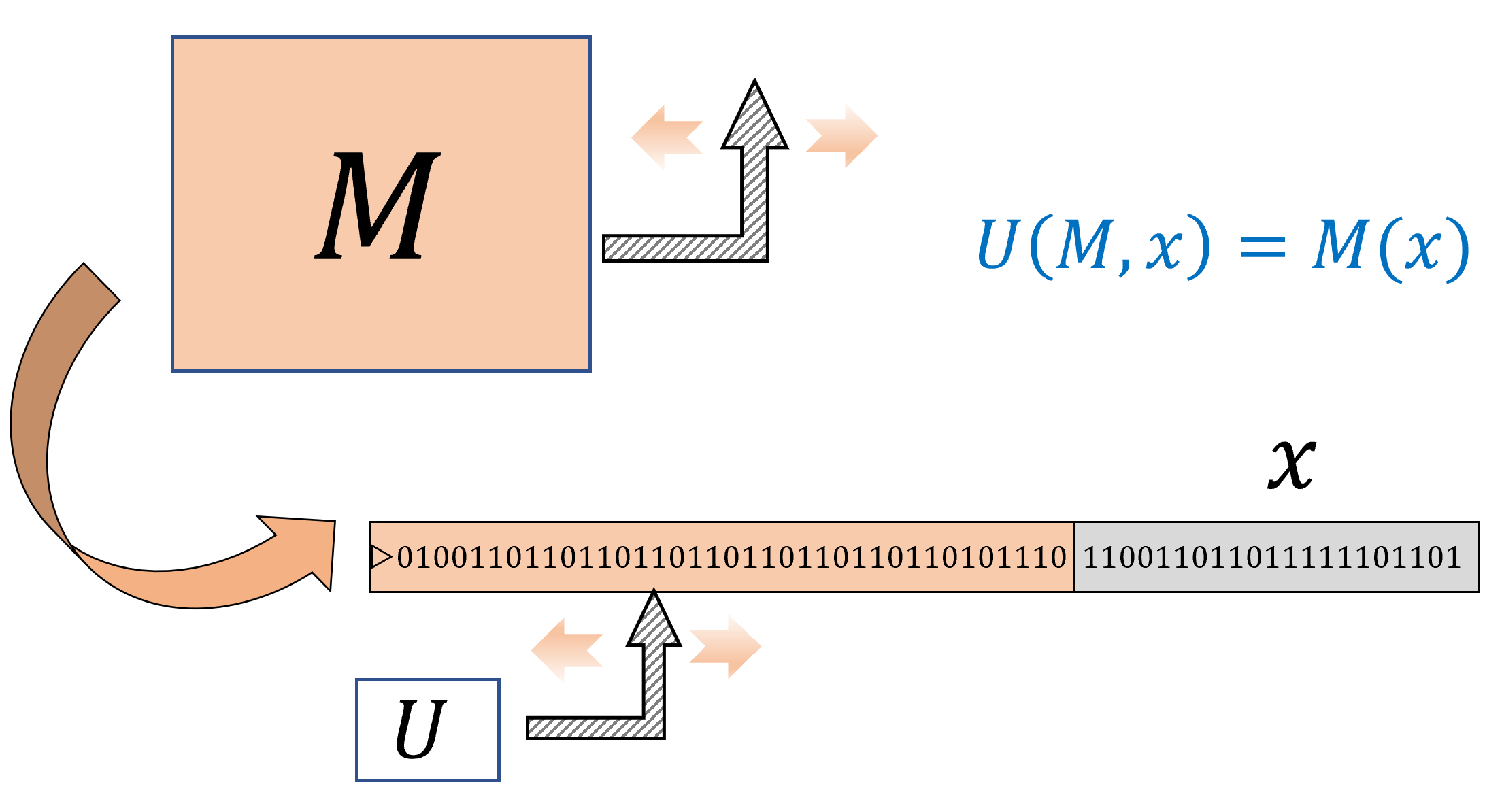
There is a “universal” algorithm that can evaluate arbitrary algorithms on arbitrary inputs.
Once you understand what the theorem says, it is not that hard to prove. The desired program \(U\) is an interpreter for Turing machines. That is, \(U\) gets a representation of the machine \(M\) (think of it as source code), and some input \(x\), and needs to simulate the execution of \(M\) on \(x\).
Think of how you would code \(U\) in your favorite programming language. First, you would need to decide on some representation scheme for \(M\). For example, you can use an array or a dictionary to encode \(M\)’s transition function. Then you would use some data structure, such as a list, to store the contents of \(M\)’s tape. Now you can simulate \(M\) step by step, updating the data structure as you go along. The interpreter will continue the simulation until the machine halts.
Once you do that, translating this interpreter from your favorite programming language to a Turing machine can be done just as we have seen in Chapter 8. The end result is what’s known as a “meta-circular evaluator”: an interpreter for a programming language in the same one. This is a concept that has a long history in computer science starting from the original universal Turing machine. See also Figure 9.3.
Proving the existence of a universal Turing Machine
To prove (and even properly state) Theorem 9.1, we need to fix some representation for Turing machines as strings. One potential choice for such a representation is to use the equivalence between Turing machines and NAND-TM programs and hence represent a Turing machine \(M\) using the ASCII encoding of the source code of the corresponding NAND-TM program \(P\). However, we will use a more direct encoding.
Let \(M\) be a Turing machine with \(k\) states and a size \(\ell\) alphabet \(\Sigma = \{ \sigma_0,\ldots,\sigma_{\ell-1} \}\) (we use the convention \(\sigma_0 = 0\), \(\sigma_1 = 1\), \(\sigma_2 = \varnothing\), \(\sigma_3=\triangleright\)). We represent \(M\) as the triple \((k,\ell,T)\) where \(T\) is the table of values for \(\delta_M\):
where each value \(\delta_M(s,\sigma)\) is a triple \((s',\sigma',d)\) with \(s'\in [k]\), \(\sigma'\in \Sigma\) and \(d\) a number \(\{0,1,2,3 \}\) encoding one of \(\{ \mathsf{L},\mathsf{R},\mathsf{S},\mathsf{H} \}\). Thus such a machine \(M\) is encoded by a list of \(2 + 3k\cdot\ell\) natural numbers. The string representation of \(M\) is obtained by concatenating a prefix free representation of all these integers. If a string \(\alpha \in \{0,1\}^*\) does not represent a list of integers in the form above, then we treat it as representing the trivial Turing machine with one state that immediately halts on every input.
The details of the representation scheme of Turing machines as strings are immaterial for almost all applications. What you need to remember are the following points:
We can represent every Turing machine as a string.
Given the string representation of a Turing machine \(M\) and an input \(x\), we can simulate \(M\)’s execution on the input \(x\). (This is the content of Theorem 9.1.)
An additional minor issue is that for convenience we make the assumption that every string represents some Turing machine. This is very easy to ensure by just mapping strings that would otherwise not represent a Turing machine into some fixed trivial machine. This assumption is not very important, but does make a few results (such as Rice’s Theorem: Theorem 9.15) a little less cumbersome to state.
Using this representation, we can formally prove Theorem 9.1.
We will only sketch the proof, giving the major ideas. First, we observe that we can easily write a Python program that, on input a representation \((k,\ell,T)\) of a Turing machine \(M\) and an input \(x\), evaluates \(M\) on \(X\). Here is the code of this program for concreteness, though you can feel free to skip it if you are not familiar with (or interested in) Python:
# constants
def EVAL(δ,x):
'''Evaluate TM given by transition table δ
on input x'''
Tape = ["▷"] + [a for a in x]
i = 0; s = 0 # i = head pos, s = state
while True:
s, Tape[i], d = δ[(s,Tape[i])]
if d == "H": break
if d == "L": i = max(i-1,0)
if d == "R": i += 1
if i>= len(Tape): Tape.append('Φ')
j = 1; Y = [] # produce output
while Tape[j] != 'Φ':
Y.append(Tape[j])
j += 1
return YOn input a transition table \(\delta\) this program will simulate the corresponding machine \(M\) step by step, at each point maintaining the invariant that the array Tape contains the contents of \(M\)’s tape, and the variable s contains \(M\)’s current state.
The above does not prove the theorem as stated, since we need to show a Turing machine that computes \(\ensuremath{\mathit{EVAL}}\) rather than a Python program. With enough effort, we can translate this Python code line by line to a Turing machine. However, to prove the theorem we don’t need to do this, but can use our “eat the cake and have it too” paradigm. That is, while we need to evaluate a Turing machine, in writing the code for the interpreter we are allowed to use a richer model such as NAND-RAM since it is equivalent in power to Turing machines per Theorem 8.1.
Translating the above Python code to NAND-RAM is truly straightforward. The only issue is that NAND-RAM doesn’t have the dictionary data structure built in, which we have used above to store the transition function δ. However, we can represent a dictionary \(D\) of the form \(\{ key_0:val_0 , \ldots, key_{m-1}:val_{m-1} \}\) as simply a list of pairs. To compute \(D[k]\) we can scan over all the pairs until we find one of the form \((k,v)\) in which case we return \(v\). Similarly we scan the list to update the dictionary with a new value, either modifying it or appending the pair \((key,val)\) at the end.
The argument in the proof of Theorem 9.1 is a very inefficient way to implement the dictionary data structure in practice, but it suffices for the purpose of proving the theorem. Reading and writing to a dictionary of \(m\) values in this implementation takes \(\Omega(m)\) steps, but it is in fact possible to do this in \(O(\log m)\) steps using a search tree data structure or even \(O(1)\) (for “typical” instances) using a hash table. NAND-RAM and RAM machines correspond to the architecture of modern electronic computers, and so we can implement hash tables and search trees in NAND-RAM just as they are implemented in other programming languages.
The construction above yields a universal Turing machine with a very large number of states. However, since universal Turing machines have such a philosophical and technical importance, researchers have attempted to find the smallest possible universal Turing machines, see Section 9.7.
Implications of universality (discussion)

There is more than one Turing machine \(U\) that satisfies the conditions of Theorem 9.1, but the existence of even a single such machine is already extremely fundamental to both the theory and practice of computer science. Theorem 9.1’s impact reaches beyond the particular model of Turing machines. Because we can simulate every Turing machine by a NAND-TM program and vice versa, Theorem 9.1 immediately implies there exists a universal NAND-TM program \(P_U\) such that \(P_U(P,x)=P(x)\) for every NAND-TM program \(P\). We can also “mix and match” models. For example since we can simulate every NAND-RAM program by a Turing machine, and every Turing machine by the \(\lambda\) calculus, Theorem 9.1 implies that there exists a \(\lambda\) expression \(e\) such that for every NAND-RAM program \(P\) and input \(x\) on which \(P(x)=y\), if we encode \((P,x)\) as a \(\lambda\)-expression \(f\) (using the \(\lambda\)-calculus encoding of strings as lists of \(0\)’s and \(1\)’s) then \((e\; f)\) evaluates to an encoding of \(y\). More generally we can say that for every \(\mathcal{X}\) and \(\mathcal{Y}\) in the set \(\{\) Turing machines, RAM Machines, NAND-TM, NAND-RAM, \(\lambda\)-calculus, JavaScript, Python, \(\ldots\) \(\}\) of Turing equivalent models, there exists a program/machine in \(\mathcal{X}\) that computes the map \((P,x) \mapsto P(x)\) for every program/machine \(P \in \mathcal{Y}\).
The idea of a “universal program” is of course not limited to theory. For example compilers for programming languages are often used to compile themselves, as well as programs more complicated than the compiler. (An extreme example of this is Fabrice Bellard’s Obfuscated Tiny C Compiler which is a C program of 2048 bytes that can compile a large subset of the C programming language, and in particular can compile itself.) This is also related to the fact that it is possible to write a program that can print its own source code, see Figure 9.3. There are universal Turing machines known that require a very small number of states or alphabet symbols, and in particular there is a universal Turing machine (with respect to a particular choice of representing Turing machines as strings) whose tape alphabet is \(\{ \triangleright, \varnothing, 0, 1 \}\) and has fewer than \(25\) states (see Section 9.7).
Is every function computable?
In Theorem 4.12, we saw that NAND-CIRC programs can compute every finite function \(f:\{0,1\}^n \rightarrow \{0,1\}\). Therefore a natural guess is that NAND-TM programs (or equivalently, Turing machines) could compute every infinite function \(F:\{0,1\}^* \rightarrow \{0,1\}\). However, this turns out to be false. That is, there exists a function \(F:\{0,1\}^* \rightarrow \{0,1\}\) that is uncomputable!
The existence of uncomputable functions is quite surprising. Our intuitive notion of a “function” (and the notion most mathematicians had until the 20th century) is that a function \(f\) defines some implicit or explicit way of computing the output \(f(x)\) from the input \(x\). The notion of an “uncomputable function” thus seems to be a contradiction in terms, but yet the following theorem shows that such creatures do exist:
There exists a function \(F^*:\{0,1\}^* \rightarrow \{0,1\}\) that is not computable by any Turing machine.
The idea behind the proof follows quite closely Cantor’s proof that the reals are uncountable (Theorem 2.5), and in fact the theorem can also be obtained fairly directly from that result (see Exercise 7.11). However, it is instructive to see the direct proof. The idea is to construct \(F^*\) in a way that will ensure that every possible machine \(M\) will in fact fail to compute \(F^*\). We do so by defining \(F^*(x)\) to equal \(0\) if \(x\) describes a Turing machine \(M\) which satisfies \(M(x)=1\) and defining \(F^*(x)=1\) otherwise. By construction, if \(M\) is any Turing machine and \(x\) is the string describing it, then \(F^*(x) \neq M(x)\) and therefore \(M\) does not compute \(F^*\).
The proof is illustrated in Figure 9.4. We start by defining the following function \(G:\{0,1\}^* \rightarrow \{0,1\}\):
For every string \(x\in\{0,1\}^*\), if \(x\) satisfies (1) \(x\) is a valid representation of some Turing machine \(M\) (per the representation scheme above) and (2) when the program \(M\) is executed on the input \(x\) it halts and produces an output, then we define \(G(x)\) as the first bit of this output. Otherwise (i.e., if \(x\) is not a valid representation of a Turing machine, or the machine \(M_x\) never halts on \(x\)) we define \(G(x)=0\). We define \(F^*(x) = 1 - G(x)\).
We claim that there is no Turing machine that computes \(F^*\). Indeed, suppose, towards the sake of contradiction, there exists a machine \(M\) that computes \(F^*\), and let \(x\) be the binary string that represents the machine \(M\). On one hand, since by our assumption \(M\) computes \(F^*\), on input \(x\) the machine \(M\) halts and outputs \(F^*(x)\). On the other hand, by the definition of \(F^*\), since \(x\) is the representation of the machine \(M\), \(F^*(x) = 1 - G(x) = 1 - M(x)\), hence yielding a contradiction.
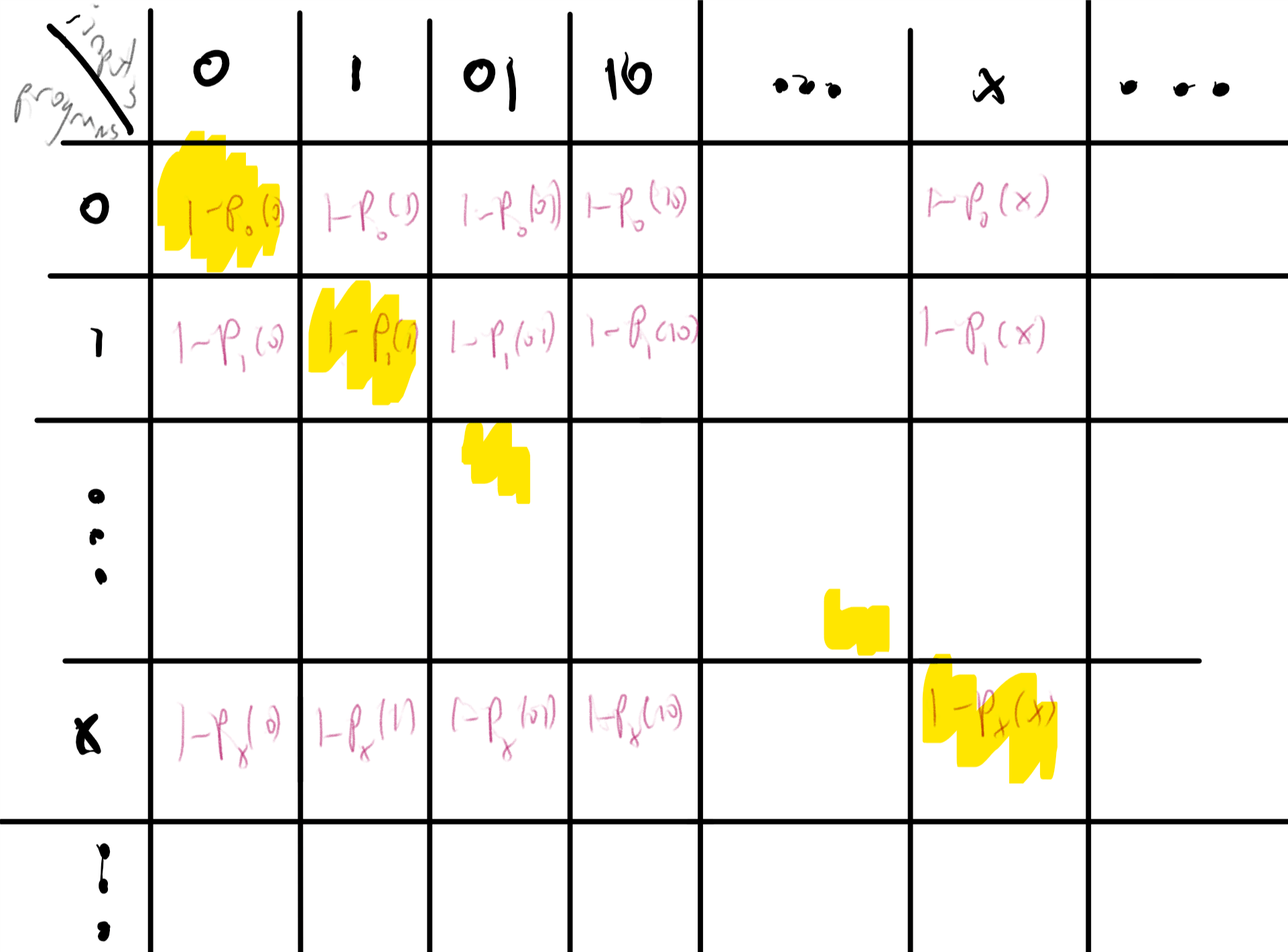
There are some functions that can not be computed by any algorithm.
The proof of Theorem 9.5 is short but subtle. I suggest that you pause here and go back to read it again and think about it - this is a proof that is worth reading at least twice if not three or four times. It is not often the case that a few lines of mathematical reasoning establish a deeply profound fact - that there are problems we simply cannot solve.
The type of argument used to prove Theorem 9.5 is known as diagonalization since it can be described as defining a function based on the diagonal entries of a table as in Figure 9.4. The proof can be thought of as an infinite version of the counting argument we used for showing lower bound for NAND-CIRC programs in Theorem 5.3. Namely, we show that it’s not possible to compute all functions from \(\{0,1\}^* \rightarrow \{0,1\}\) by Turing machines simply because there are more functions like that than there are Turing machines.
As mentioned in Remark 7.4, many texts use the “language” terminology and so will call a set \(L \subseteq \{0,1\}^*\) an undecidable or non-recursive language if the function \(F:\{0,1\}^* \rightarrow \{0,1\}\) such that \(F(x)=1 \leftrightarrow x\in L\) is uncomputable.
The Halting problem
Theorem 9.5 shows that there is some function that cannot be computed. But is this function the equivalent of the “tree that falls in the forest with no one hearing it”? That is, perhaps it is a function that no one actually wants to compute. It turns out that there are natural uncomputable functions:
Let \(\ensuremath{\mathit{HALT}}:\{0,1\}^* \rightarrow \{0,1\}\) be the function such that for every string \(M\in \{0,1\}^*\), \(\ensuremath{\mathit{HALT}}(M,x)=1\) if Turing machine \(M\) halts on the input \(x\) and \(\ensuremath{\mathit{HALT}}(M,x)=0\) otherwise. Then \(\ensuremath{\mathit{HALT}}\) is not computable.
Before turning to prove Theorem 9.6, we note that \(\ensuremath{\mathit{HALT}}\) is a very natural function to want to compute. For example, one can think of \(\ensuremath{\mathit{HALT}}\) as a special case of the task of managing an “App store”. That is, given the code of some application, the gatekeeper for the store needs to decide if this code is safe enough to allow in the store or not. At a minimum, it seems that we should verify that the code would not go into an infinite loop.
One way to think about this proof is as follows:
If a function \(F\) is uncomputable we can show that another function \(H\) is uncomputable by giving a way to reduce the task of computing \(F\) to computing \(H\).
The proof will use the previously established result Theorem 9.5. Recall that Theorem 9.5 shows that the following function \(F^*: \{0,1\}^* \rightarrow \{0,1\}\) is uncomputable:
We will show that the uncomputability of \(F^*\) implies the uncomputability of \(\ensuremath{\mathit{HALT}}\). Specifically, we will assume, towards a contradiction, that there exists a Turing machine \(M\) that can compute the \(\ensuremath{\mathit{HALT}}\) function, and use that to obtain a Turing machine \(M'\) that computes the function \(F^*\). (This is known as a proof by reduction, since we reduce the task of computing \(F^*\) to the task of computing \(\ensuremath{\mathit{HALT}}\). By the contrapositive, this means the uncomputability of \(F^*\) implies the uncomputability of \(\ensuremath{\mathit{HALT}}\).)
Indeed, suppose that \(M\) is a Turing machine that computes \(\ensuremath{\mathit{HALT}}\). Algorithm 9.7 describes a Turing machine \(M'\) that computes \(F^*\). (We use “high level” description of Turing machines, appealing to the “have your cake and eat it too” paradigm, see Big Idea 10.)
Algorithm 9.7 F^* to HALT reduction
Input: \(x\in \{0,1\}^*\)
Output: \(F^*(x)\)
# Assume T.M. \(M_{HALT}\) computes \(HALT\)
Let \(z \leftarrow M_{HALT}(x,x)\). # Assume \(z=HALT(x,x)\).
if{\(z=0\)}
return \(1\)
endif
Let \(y \leftarrow U(x,x)\) # \(U\) universal TM, i.e., \(y=x(x)\)
if{\(y=1\)}
return \(0\)
endif
return \(1\)
We claim that Algorithm 9.7 computes the function \(F^*\). Indeed, suppose that \(x(x)=1\) (and hence \(F^*(x)=0\)). In this case, \(\ensuremath{\mathit{HALT}}(x,x)=1\) and hence, under our assumption that \(M(x,x)=\ensuremath{\mathit{HALT}}(x,x)\), the value \(z\) will equal \(1\), and hence Algorithm 9.7 will set \(y=x(x)=1\), and output the correct value \(0\).
Suppose otherwise that \(x(x) \neq 1\) (and hence \(F^*(x)=1\)). In this case there are two possibilities:
Case 1: The machine described by \(x\) does not halt on the input \(x\) (and hence \(F^*(x)=1\)). In this case, \(\ensuremath{\mathit{HALT}}(x,x)=0\). Since we assume that \(M\) computes \(\ensuremath{\mathit{HALT}}\) it means that on input \(x,x\), the machine \(M\) must halt and output the value \(0\). This means that Algorithm 9.7 will set \(z=0\) and output \(1\).
Case 2: The machine described by \(x\) halts on the input \(x\) and outputs some \(y' \neq 1\) (and hence \(F^*(x)=0\)). In this case, since \(\ensuremath{\mathit{HALT}}(x,x)=1\), under our assumptions, Algorithm 9.7 will set \(y=y' \neq 1\) and so output \(1\).
We see that in all cases, \(M'(x)=F^*(x)\), which contradicts the fact that \(F^*\) is uncomputable. Hence we reach a contradiction to our original assumption that \(M\) computes \(\ensuremath{\mathit{HALT}}\).
Once again, this is a proof that’s worth reading more than once. The uncomputability of the halting problem is one of the fundamental theorems of computer science, and is the starting point for much of the investigations we will see later. An excellent way to get a better understanding of Theorem 9.6 is to go over Section 9.3.2, which presents an alternative proof of the same result.
Is the Halting problem really hard? (discussion)
Many people’s first instinct when they see the proof of Theorem 9.6 is to not believe it. That is, most people do believe the mathematical statement, but intuitively it doesn’t seem that the Halting problem is really that hard. After all, being uncomputable only means that \(\ensuremath{\mathit{HALT}}\) cannot be computed by a Turing machine.
But programmers seem to solve \(\ensuremath{\mathit{HALT}}\) all the time by informally or formally arguing that their programs halt. It’s true that their programs are written in C or Python, as opposed to Turing machines, but that makes no difference: we can easily translate back and forth between this model and any other programming language.
While every programmer encounters at some point an infinite loop, is there really no way to solve the halting problem? Some people argue that they personally can, if they think hard enough, determine whether any concrete program that they are given will halt or not. Some have even argued that humans in general have the ability to do that, and hence humans have inherently superior intelligence to computers or anything else modeled by Turing machines.1
The best answer we have so far is that there truly is no way to solve \(\ensuremath{\mathit{HALT}}\), whether using Macs, PCs, quantum computers, humans, or any other combination of electronic, mechanical, and biological devices. Indeed this assertion is the content of the Church-Turing Thesis. This of course does not mean that for every possible program \(P\), it is hard to decide if \(P\) enters an infinite loop. Some programs don’t even have loops at all (and hence trivially halt), and there are many other far less trivial examples of programs that we can certify to never enter an infinite loop (or programs that we know for sure that will enter such a loop). However, there is no general procedure that would determine for an arbitrary program \(P\) whether it halts or not. Moreover, there are some very simple programs for which no one knows whether they halt or not. For example, the following Python program will halt if and only if Goldbach’s conjecture is false:
def isprime(p):
return all(p % i for i in range(2,p-1))
def Goldbach(n):
return any( (isprime(p) and isprime(n-p))
for p in range(2,n-1))
n = 4
while True:
if not Goldbach(n): break
n+= 2Given that Goldbach’s Conjecture has been open since 1742, it is unclear that humans have any magical ability to say whether this (or other similar programs) will halt or not.

A direct proof of the uncomputability of \(\ensuremath{\mathit{HALT}}\) (optional)
It turns out that we can combine the ideas of the proofs of Theorem 9.5 and Theorem 9.6 to obtain a short proof of the latter theorem, that does not appeal to the uncomputability of \(F^*\). This short proof appeared in print in a 1965 letter to the editor of Christopher Strachey:
To the Editor, The Computer Journal.
An Impossible Program
Sir,
A well-known piece of folk-lore among programmers holds that it is impossible to write a program which can examine any other program and tell, in every case, if it will terminate or get into a closed loop when it is run. I have never actually seen a proof of this in print, and though Alan Turing once gave me a verbal proof (in a railway carriage on the way to a Conference at the NPL in 1953), I unfortunately and promptly forgot the details. This left me with an uneasy feeling that the proof must be long or complicated, but in fact it is so short and simple that it may be of interest to casual readers. The version below uses CPL, but not in any essential way.
Suppose
T[R]is a Boolean function taking a routine (or program)Rwith no formal or free variables as its arguments and that for allR,T[R] = TrueifRterminates if run and thatT[R] = FalseifRdoes not terminate.Consider the routine P defined as follows
rec routine P
§L: if T[P] go to L
Return §
If
T[P] = Truethe routinePwill loop, and it will only terminate ifT[P] = False. In each caseT[P]has exactly the wrong value, and this contradiction shows that the function T cannot exist.Yours faithfully,
C. StracheyChurchill College, Cambridge
Try to stop and extract the argument for proving Theorem 9.6 from the letter above.
Since CPL is not as common today, let us reproduce this proof. The idea is the following: suppose for the sake of contradiction that there exists a program T such that T(f,x) equals True iff f halts on input x. (Strachey’s letter considers the no-input variant of \(\ensuremath{\mathit{HALT}}\), but as we’ll see, this is an immaterial distinction.) Then we can construct a program P and an input x such that T(P,x) gives the wrong answer. The idea is that on input x, the program P will do the following: run T(x,x), and if the answer is True then go into an infinite loop, and otherwise halt. Now you can see that T(P,P) will give the wrong answer: if P halts when it gets its own code as input, then T(P,P) is supposed to be True, but then P(P) will go into an infinite loop. And if P does not halt, then T(P,P) is supposed to be False but then P(P) will halt. We can also code this up in Python:
def CantSolveMe(T):
"""
Gets function T that claims to solve HALT.
Returns a pair (P,x) of code and input on which
T(P,x) ≠ HALT(x)
"""
def fool(x):
if T(x,x):
while True: pass
return "I halted"
return (fool,fool)For example, consider the following Naive Python program T that guesses that a given function does not halt if its input contains while or for
def T(f,x):
"""Crude halting tester - decides it doesn't halt if it contains a loop."""
import inspect
source = inspect.getsource(f)
if source.find("while"): return False
if source.find("for"): return False
return TrueIf we now set (f,x) = CantSolveMe(T), then T(f,x)=False but f(x) does in fact halt. This is of course not specific to this particular T: for every program T, if we run (f,x) = CantSolveMe(T) then we’ll get an input on which T gives the wrong answer to \(\ensuremath{\mathit{HALT}}\).
Reductions
The Halting problem turns out to be a linchpin of uncomputability, in the sense that Theorem 9.6 has been used to show the uncomputability of a great many interesting functions. We will see several examples of such results in this chapter and the exercises, but there are many more such results (see Figure 9.6).
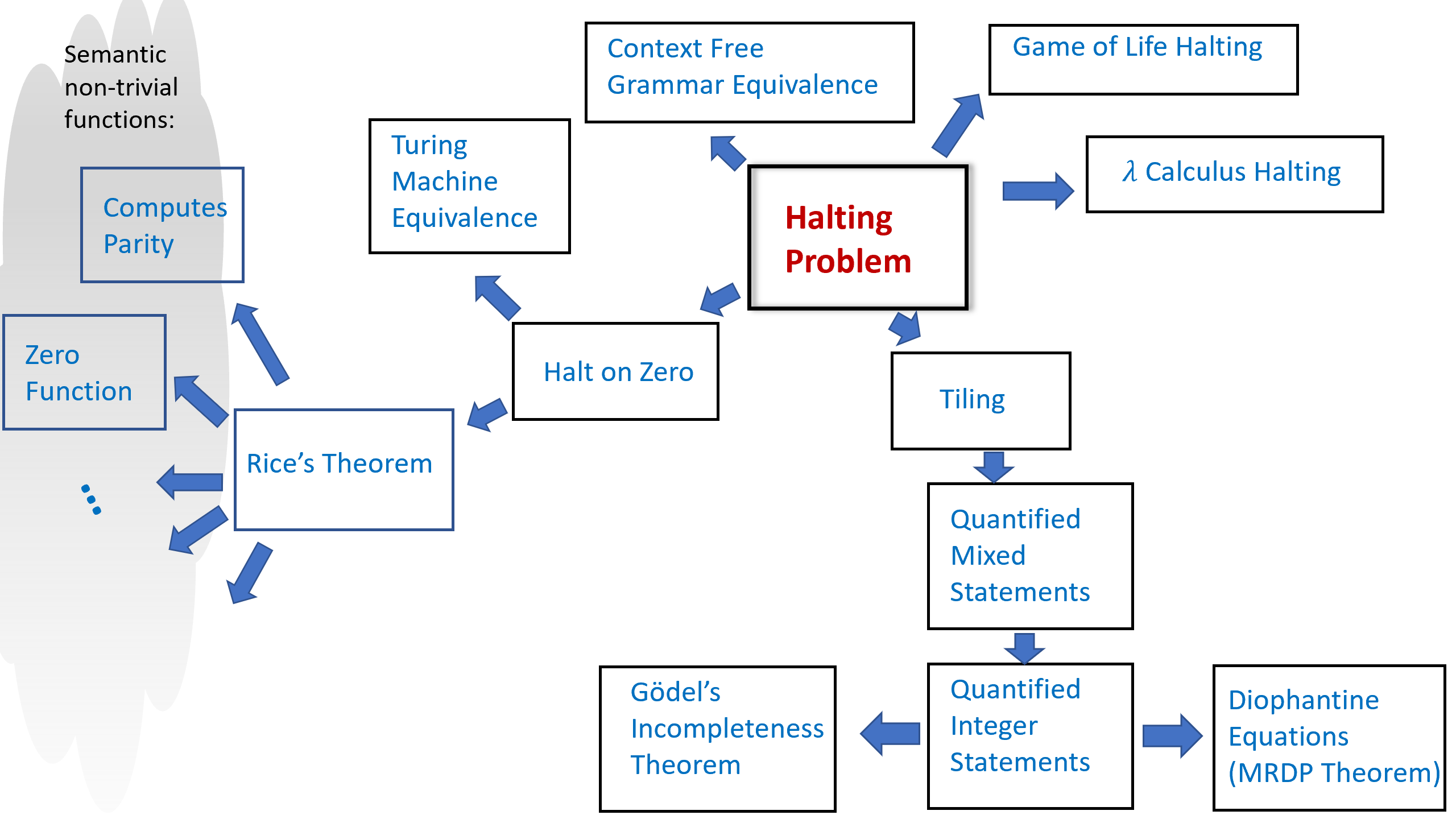
The idea behind such uncomputability results is conceptually simple but can at first be quite confusing. If we know that \(\ensuremath{\mathit{HALT}}\) is uncomputable, and we want to show that some other function \(\ensuremath{\mathit{BLAH}}\) is uncomputable, then we can do so via a contrapositive argument (i.e., proof by contradiction). That is, we show that if there exists a Turing machine that computes \(\ensuremath{\mathit{BLAH}}\) then there exists a Turing machine that computes \(\ensuremath{\mathit{HALT}}\). (Indeed, this is exactly how we showed that \(\ensuremath{\mathit{HALT}}\) itself is uncomputable, by deriving this fact from the uncomputability of the function \(F^*\) of Theorem 9.5.)
For example, to prove that \(\ensuremath{\mathit{BLAH}}\) is uncomputable, we could show that there is a computable function \(R:\{0,1\}^* \rightarrow \{0,1\}^*\) such that for every pair \(M\) and \(x\), \(\ensuremath{\mathit{HALT}}(M,x)=\ensuremath{\mathit{BLAH}}(R(M,x))\). The existence of such a function \(R\) implies that if \(\ensuremath{\mathit{BLAH}}\) was computable then \(\ensuremath{\mathit{HALT}}\) would be computable as well, hence leading to a contradiction! The confusing part about reductions is that we are assuming something we believe is false (that \(\ensuremath{\mathit{BLAH}}\) has an algorithm) to derive something that we know is false (that \(\ensuremath{\mathit{HALT}}\) has an algorithm). Michael Sipser describes such results as having the form “If pigs could whistle then horses could fly”.
A reduction-based proof has two components. For starters, since we need \(R\) to be computable, we should describe the algorithm to compute it. The algorithm to compute \(R\) is known as a reduction since the transformation \(R\) modifies an input to \(\ensuremath{\mathit{HALT}}\) to an input to \(\ensuremath{\mathit{BLAH}}\), and hence reduces the task of computing \(\ensuremath{\mathit{HALT}}\) to the task of computing \(\ensuremath{\mathit{BLAH}}\). The second component of a reduction-based proof is the analysis of the algorithm \(R\): namely a proof that \(R\) does indeed satisfy the desired properties.
Reduction-based proofs are just like other proofs by contradiction, but the fact that they involve hypothetical algorithms that don’t really exist tends to make reductions quite confusing. The one silver lining is that at the end of the day the notion of reductions is mathematically quite simple, and so it’s not that bad even if you have to go back to first principles every time you need to remember what is the direction that a reduction should go in.
A reduction is an algorithm, which means that, as discussed in Remark 0.3, a reduction has three components:
Specification (what): In the case of a reduction from \(\ensuremath{\mathit{HALT}}\) to \(\ensuremath{\mathit{BLAH}}\), the specification is that function \(R:\{0,1\}^* \rightarrow \{0,1\}^*\) should satisfy that \(\ensuremath{\mathit{HALT}}(M,x)=\ensuremath{\mathit{BLAH}}(R(M,x))\) for every Turing machine \(M\) and input \(x\). In general, to reduce a function \(F\) to \(G\), the reduction should satisfy \(F(w)=G(R(w))\) for every input \(w\) to \(F\).
Implementation (how): The algorithm’s description: the precise instructions how to transform an input \(w\) to the output \(y=R(w)\).
Analysis (why): A proof that the algorithm meets the specification. In particular, in a reduction from \(F\) to \(G\) this is a proof that for every input \(w\), the output \(y=R(w)\) of the algorithm satisfies that \(F(w)=G(y)\).
Example: Halting on the zero problem
Here is a concrete example for a proof by reduction. We define the function \(\ensuremath{\mathit{HALTONZERO}}:\{0,1\}^* \rightarrow \{0,1\}\) as follows. Given any string \(M\), \(\ensuremath{\mathit{HALTONZERO}}(M)=1\) if and only if \(M\) describes a Turing machine that halts when it is given the string \(0\) as input. A priori \(\ensuremath{\mathit{HALTONZERO}}\) seems like a potentially easier function to compute than the full-fledged \(\ensuremath{\mathit{HALT}}\) function, and so we could perhaps hope that it is not uncomputable. Alas, the following theorem shows that this is not the case:
\(\ensuremath{\mathit{HALTONZERO}}\) is uncomputable.
The proof of Theorem 9.9 is below, but before reading it you might want to pause for a couple of minutes and think how you would prove it yourself. In particular, try to think of what a reduction from \(\ensuremath{\mathit{HALT}}\) to \(\ensuremath{\mathit{HALTONZERO}}\) would look like. Doing so is an excellent way to get some initial comfort with the notion of proofs by reduction, which a technique we will be using time and again in this book. You can also see Figure 9.8 and the following Colab notebook for a Python implementation of this reduction.
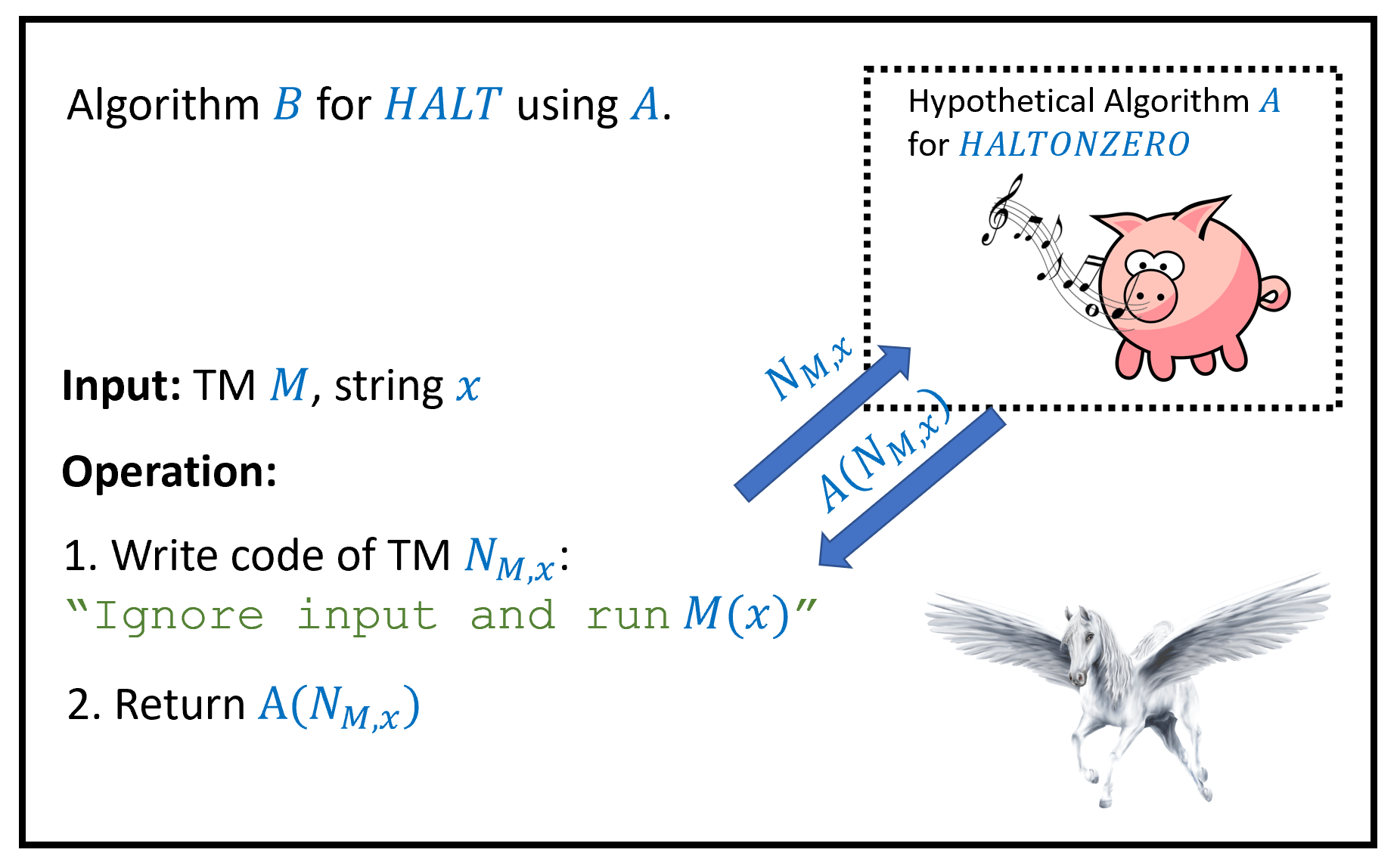
The proof is by reduction from \(\ensuremath{\mathit{HALT}}\), see Figure 9.7. We will assume, towards the sake of contradiction, that \(\ensuremath{\mathit{HALTONZERO}}\) is computable by some algorithm \(A\), and use this hypothetical algorithm \(A\) to construct an algorithm \(B\) to compute \(\ensuremath{\mathit{HALT}}\), hence obtaining a contradiction to Theorem 9.6. (As discussed in Big Idea 10, following our “have your cake and eat it too” paradigm, we just use the generic name “algorithm” rather than worrying whether we model them as Turing machines, NAND-TM programs, NAND-RAM, etc.; this makes no difference since all these models are equivalent to one another.)
Since this is our first proof by reduction from the Halting problem, we will spell it out in more details than usual. Such a proof by reduction consists of two steps:
Description of the reduction: We will describe the operation of our algorithm \(B\), and how it makes “function calls” to the hypothetical algorithm \(A\).
Analysis of the reduction: We will then prove that under the hypothesis that Algorithm \(A\) computes \(\ensuremath{\mathit{HALTONZERO}}\), Algorithm \(B\) will compute \(\ensuremath{\mathit{HALT}}\).
Algorithm 9.10 HALT to HALTONZERO reduction
Input: Turing machine \(M\) and string \(x\).
Output: Turing machine \(M'\) such that \(M\) halts on \(x\) iff \(M'\) halts on zero
Procedure{\(N_{M,x}\)}{\(w\)} # Description of the T.M. \(N_{M,x}\)
return \(EVAL(M,x)\) # Ignore the Input: \(w\), evaluate \(M\) on \(x\).
endproc
return \(N_{M,x}\) # We do not execute \(N_{M,x}\): only return its description
Our Algorithm \(B\) works as follows: on input \(M,x\), it runs Algorithm 9.10 to obtain a Turing machine \(M'\), and then returns \(A(M')\). The machine \(M'\) ignores its input \(z\) and simply runs \(M\) on \(x\).
In pseudocode, the program \(N_{M,x}\) will look something like the following:
def N(z):
M = r'.......'
# a string constant containing desc. of M
x = r'.......'
# a string constant containing x
return eval(M,x)
# note that we ignore the input zThat is, if we think of \(N_{M,x}\) as a program, then it is a program that contains \(M\) and \(x\) as “hardwired constants”, and given any input \(z\), it simply ignores the input and always returns the result of evaluating \(M\) on \(x\). The algorithm \(B\) does not actually execute the machine \(N_{M,x}\). \(B\) merely writes down the description of \(N_{M,x}\) as a string (just as we did above) and feeds this string as input to \(A\).
The above completes the description of the reduction. The analysis is obtained by proving the following claim:
Claim: For every strings \(M,x,z\), the machine \(N_{M,x}\) constructed by Algorithm \(B\) in Step 1 satisfies that \(N_{M,x}\) halts on \(z\) if and only if the program described by \(M\) halts on the input \(x\).
Proof of Claim: Since \(N_{M,x}\) ignores its input and evaluates \(M\) on \(x\) using the universal Turing machine, it will halt on \(z\) if and only if \(M\) halts on \(x\).
In particular if we instantiate this claim with the input \(z=0\) to \(N_{M,x}\), we see that \(\ensuremath{\mathit{HALTONZERO}}(N_{M,x})=\ensuremath{\mathit{HALT}}(M,x)\). Thus if the hypothetical algorithm \(A\) satisfies \(A(M)=\ensuremath{\mathit{HALTONZERO}}(M)\) for every \(M\) then the algorithm \(B\) we construct satisfies \(B(M,x)=\ensuremath{\mathit{HALT}}(M,x)\) for every \(M,x\), contradicting the uncomputability of \(\ensuremath{\mathit{HALT}}\).

In the proof of Theorem 9.9 we used the technique of “hardwiring” an input \(x\) to a program/machine \(P\). That is, we take a program that computes the function \(x \mapsto f(x)\) and “fix” or “hardwire” some of the inputs to some constant value. For example, if you have a program that takes as input a pair of numbers \(x,y\) and outputs their product (i.e., computes the function \(f(x,y) =x\times y\)), then you can “hardwire” the second input to be \(17\) and obtain a program that takes as input a number \(x\) and outputs \(x\times 17\) (i.e., computes the function \(g(x) = x\times 17\)). This technique is quite common in reductions and elsewhere, and we will use it time and again in this book.
Rice’s Theorem and the impossibility of general software verification
The uncomputability of the Halting problem turns out to be a special case of a much more general phenomenon. Namely, that we cannot certify semantic properties of general purpose programs. “Semantic properties” mean properties of the function that the program computes, as opposed to properties that depend on the particular syntax used by the program.
An example for a semantic property of a program \(P\) is the property that whenever \(P\) is given an input string with an even number of \(1\)’s, it outputs \(0\). Another example is the property that \(P\) will always halt whenever the input ends with a \(1\). In contrast, the property that a C program contains a comment before every function declaration is not a semantic property, since it depends on the actual source code as opposed to the input/output relation.
Checking semantic properties of programs is of great interest, as it corresponds to checking whether a program conforms to a specification. Alas it turns out that such properties are in general uncomputable. We have already seen some examples of uncomputable semantic functions, namely \(\ensuremath{\mathit{HALT}}\) and \(\ensuremath{\mathit{HALTONZERO}}\), but these are just the “tip of the iceberg”. We start by observing one more such example:
Let \(\ensuremath{\mathit{ZEROFUNC}}:\{0,1\}^* \rightarrow \{0,1\}\) be the function such that for every \(M\in \{0,1\}^*\), \(\ensuremath{\mathit{ZEROFUNC}}(M)=1\) if and only if \(M\) represents a Turing machine such that \(M\) outputs \(0\) on every input \(x\in \{0,1\}^*\). Then \(\ensuremath{\mathit{ZEROFUNC}}\) is uncomputable.
Despite the similarity in their names, \(\ensuremath{\mathit{ZEROFUNC}}\) and \(\ensuremath{\mathit{HALTONZERO}}\) are two different functions. For example, if \(M\) is a Turing machine that on input \(x \in \{0,1\}^*\), halts and outputs the OR of all of \(x\)’s coordinates, then \(\ensuremath{\mathit{HALTONZERO}}(M)=1\) (since \(M\) does halt on the input \(0\)) but \(\ensuremath{\mathit{ZEROFUNC}}(M)=0\) (since \(M\) does not compute the constant zero function).
The proof is by reduction from \(\ensuremath{\mathit{HALTONZERO}}\). Suppose, towards the sake of contradiction, that there was an algorithm \(A\) such that \(A(M)=\ensuremath{\mathit{ZEROFUNC}}(M)\) for every \(M \in \{0,1\}^*\). Then we will construct an algorithm \(B\) that solves \(\ensuremath{\mathit{HALTONZERO}}\), contradicting Theorem 9.9.
Given a Turing machine \(N\) (which is the input to \(\ensuremath{\mathit{HALTONZERO}}\)), our Algorithm \(B\) does the following:
Construct a Turing machine \(M\) which on input \(x\in\{0,1\}^*\), first runs \(N(0)\) and then outputs \(0\).
Return \(A(M)\).
Now if \(N\) halts on the input \(0\) then the Turing machine \(M\) computes the constant zero function, and hence under our assumption that \(A\) computes \(\ensuremath{\mathit{ZEROFUNC}}\), \(A(M)=1\). If \(N\) does not halt on the input \(0\), then the Turing machine \(M\) will not halt on any input, and so in particular will not compute the constant zero function. Hence under our assumption that \(A\) computes \(\ensuremath{\mathit{ZEROFUNC}}\), \(A(M)=0\). We see that in both cases, \(\ensuremath{\mathit{ZEROFUNC}}(M)=\ensuremath{\mathit{HALTONZERO}}(N)\) and hence the value that Algorithm \(B\) returns in step 2 is equal to \(\ensuremath{\mathit{HALTONZERO}}(N)\) which is what we needed to prove.
Another result along similar lines is the following:
The following function is uncomputable
We leave the proof of Theorem 9.13 as an exercise (Exercise 9.6). I strongly encourage you to stop here and try to solve this exercise.
Rice’s Theorem
Theorem 9.13 can be generalized far beyond the parity function. In fact, this generalization rules out verifying any type of semantic specification on programs. We define a semantic specification on programs to be some property that does not depend on the code of the program but just on the function that the program computes.
For example, consider the following two C programs
int Second(int n) {
int i = 0;
int j = 0
if (n<0) return 0;
while (j<n) {
i = i + 2;
j = j + 1;
}
return i;
}First and Second are two distinct C programs, but they compute the same function. A semantic property, would be either true for both programs or false for both programs, since it depends on the function the programs compute and not on their code. An example for a semantic property that both First and Second satisfy is the following: “The program \(P\) computes a function \(f\) mapping integers to integers satisfying that \(f(n) \geq n\) for every input \(n\)”.
A property is not semantic if it depends on the source code rather than the input/output behavior. For example, properties such as “the program contains the variable k” or “the program uses the while operation” are not semantic. Such properties can be true for one of the programs and false for others. Formally, we define semantic properties as follows:
A pair of Turing machines \(M\) and \(M'\) are functionally equivalent if for every \(x\in \{0,1\}^*\), \(M(x)=M'(x)\). (In particular, \(M(x)=\bot\) iff \(M'(x)=\bot\) for all \(x\).)
A function \(F:\{0,1\}^* \rightarrow \{0,1\}\) is semantic if for every pair of strings \(M,M'\) that represent functionally equivalent Turing machines, \(F(M)=F(M')\). (Recall that we assume that every string represents some Turing machine, see Remark 9.3)
There are two trivial examples of semantic functions: the constant one function and the constant zero function. For example, if \(Z\) is the constant zero function (i.e., \(Z(M)=0\) for every \(M\)) then clearly \(F(M)=F(M')\) for every pair of Turing machines \(M\) and \(M'\) that are functionally equivalent \(M\) and \(M'\). Here is a non-trivial example
Prove that the function \(\ensuremath{\mathit{ZEROFUNC}}\) is semantic.
Recall that \(\ensuremath{\mathit{ZEROFUNC}}(M)=1\) if and only if \(M(x)=0\) for every \(x\in \{0,1\}^*\). If \(M\) and \(M'\) are functionally equivalent, then for every \(x\), \(M(x)=M'(x)\). Hence \(\ensuremath{\mathit{ZEROFUNC}}(M)=1\) if and only if \(\ensuremath{\mathit{ZEROFUNC}}(M')=1\).
Often the properties of programs that we are most interested in computing are the semantic ones, since we want to understand the programs’ functionality. Unfortunately, Rice’s Theorem tells us that these properties are all uncomputable:
Let \(F:\{0,1\}^* \rightarrow \{0,1\}\). If \(F\) is semantic and non-trivial then it is uncomputable.
The idea behind the proof is to show that every semantic non-trivial function \(F\) is at least as hard to compute as \(\ensuremath{\mathit{HALTONZERO}}\). This will conclude the proof since by Theorem 9.9, \(\ensuremath{\mathit{HALTONZERO}}\) is uncomputable. If a function \(F\) is non-trivial then there are two machines \(M_0\) and \(M_1\) such that \(F(M_0)=0\) and \(F(M_1)=1\). So, the goal would be to take a machine \(N\) and find a way to map it into a machine \(M=R(N)\), such that (i) if \(N\) halts on zero then \(M\) is functionally equivalent to \(M_1\) and (ii) if \(N\) does not halt on zero then \(M\) is functionally equivalent to \(M_0\).
Because \(F\) is semantic, if we achieved this, then we would be guaranteed that \(\ensuremath{\mathit{HALTONZERO}}(N) = F(R(N))\), and hence would show that if \(F\) was computable, then \(\ensuremath{\mathit{HALTONZERO}}\) would be computable as well, contradicting Theorem 9.9.
We will not give the proof in full formality, but rather illustrate the proof idea by restricting our attention to a particular semantic function \(F\). However, the same techniques generalize to all possible semantic functions. Define \(\ensuremath{\mathit{MONOTONE}}:\{0,1\}^* \rightarrow \{0,1\}\) as follows: \(\ensuremath{\mathit{MONOTONE}}(M)=1\) if there does not exist \(n\in \N\) and two inputs \(x,x' \in \{0,1\}^n\) such that for every \(i\in [n]\) \(x_i \leq x'_i\) but \(M(x)\) outputs \(1\) and \(M(x')=0\). That is, \(\ensuremath{\mathit{MONOTONE}}(M)=1\) if it’s not possible to find an input \(x\) such that flipping some bits of \(x\) from \(0\) to \(1\) will change \(M\)’s output in the other direction from \(1\) to \(0\). We will prove that \(\ensuremath{\mathit{MONOTONE}}\) is uncomputable, but the proof will easily generalize to any semantic function.
We start by noting that \(\ensuremath{\mathit{MONOTONE}}\) is neither the constant zero nor the constant one function:
The machine \(\ensuremath{\mathit{INF}}\) that simply goes into an infinite loop on every input satisfies \(\ensuremath{\mathit{MONOTONE}}(\ensuremath{\mathit{INF}})=1\), since \(\ensuremath{\mathit{INF}}\) is not defined anywhere and so in particular there are no two inputs \(x,x'\) where \(x_i \leq x'_i\) for every \(i\) but \(\ensuremath{\mathit{INF}}(x)=0\) and \(\ensuremath{\mathit{INF}}(x')=1\).
The machine \(\ensuremath{\mathit{PAR}}\) that computes the XOR or parity of its input, is not monotone (e.g., \(\ensuremath{\mathit{PAR}}(1,1,0,0,\ldots,0)=0\) but \(\ensuremath{\mathit{PAR}}(1,0,0,\ldots,0)=0\)) and hence \(\ensuremath{\mathit{MONOTONE}}(\ensuremath{\mathit{PAR}})=0\).
(Note that \(\ensuremath{\mathit{INF}}\) and \(\ensuremath{\mathit{PAR}}\) are machines and not functions.)
We will now give a reduction from \(\ensuremath{\mathit{HALTONZERO}}\) to \(\ensuremath{\mathit{MONOTONE}}\). That is, we assume towards a contradiction that there exists an algorithm \(A\) that computes \(\ensuremath{\mathit{MONOTONE}}\) and we will build an algorithm \(B\) that computes \(\ensuremath{\mathit{HALTONZERO}}\). Our algorithm \(B\) will work as follows:
Algorithm \(B\):
Input: String \(N\) describing a Turing machine. (Goal: Compute \(\ensuremath{\mathit{HALTONZERO}}(N)\))
Assumption: Access to Algorithm \(A\) to compute \(\ensuremath{\mathit{MONOTONE}}\).
Operation:
Construct the following machine \(M\): “On input \(z\in \{0,1\}^*\) do: (a) Run \(N(0)\), (b) Return \(\ensuremath{\mathit{PAR}}(z)\)”.
Return \(1-A(M)\).
To complete the proof we need to show that \(B\) outputs the correct answer, under our assumption that \(A\) computes \(\ensuremath{\mathit{MONOTONE}}\). In other words, we need to show that \(\ensuremath{\mathit{HALTONZERO}}(N)=1-MONOTONE(M)\). Suppose that \(N\) does not halt on zero. In this case the program \(M\) constructed by Algorithm \(B\) enters into an infinite loop in step (a) and will never reach step (b). Hence in this case \(N\) is functionally equivalent to \(\ensuremath{\mathit{INF}}\). (The machine \(N\) is not the same machine as \(\ensuremath{\mathit{INF}}\): its description or code is different. But it does have the same input/output behavior (in this case) of never halting on any input. Also, while the program \(M\) will go into an infinite loop on every input, Algorithm \(B\) never actually runs \(M\): it only produces its code and feeds it to \(A\). Hence Algorithm \(B\) will not enter into an infinite loop even in this case.) Thus in this case, \(\ensuremath{\mathit{MONOTONE}}(M)=\ensuremath{\mathit{MONOTONE}}(\ensuremath{\mathit{INF}})=1\).
If \(N\) does halt on zero, then step (a) in \(M\) will eventually conclude and \(M\)’s output will be determined by step (b), where it simply outputs the parity of its input. Hence in this case, \(M\) computes the non-monotone parity function (i.e., is functionally equivalent to \(\ensuremath{\mathit{PAR}}\)), and so we get that \(\ensuremath{\mathit{MONOTONE}}(M)=\ensuremath{\mathit{MONOTONE}}(\ensuremath{\mathit{PAR}})=0\). In both cases, \(\ensuremath{\mathit{MONOTONE}}(M)=1-HALTONZERO(N)\), which is what we wanted to prove.
An examination of this proof shows that we did not use anything about \(\ensuremath{\mathit{MONOTONE}}\) beyond the fact that it is semantic and non-trivial. For every semantic non-trivial \(F\), we can use the same proof, replacing \(\ensuremath{\mathit{PAR}}\) and \(\ensuremath{\mathit{INF}}\) with two machines \(M_0\) and \(M_1\) such that \(F(M_0)=0\) and \(F(M_1)=1\). Such machines must exist if \(F\) is non-trivial.
Rice’s Theorem is so powerful and such a popular way of proving uncomputability that people sometimes get confused and think that it is the only way to prove uncomputability. In particular, a common misconception is that if a function \(F\) is not semantic then it is computable. This is not at all the case.
For example, consider the following function \(\ensuremath{\mathit{HALTNOYALE}}:\{0,1\}^* \rightarrow \{0,1\}\). This is a function that on input a string that represents a NAND-TM program \(P\), outputs \(1\) if and only if both (i) \(P\) halts on the input \(0\), and (ii) the program \(P\) does not contain a variable with the identifier Yale. The function \(\ensuremath{\mathit{HALTNOYALE}}\) is clearly not semantic, as it will output two different values when given as input one of the following two functionally equivalent programs:
and
However, \(\ensuremath{\mathit{HALTNOYALE}}\) is uncomputable since every program \(P\) can be transformed into an equivalent (and in fact improved :)) program \(P'\) that does not contain the variable Yale. Hence if we could compute \(\ensuremath{\mathit{HALTNOYALE}}\) then determine halting on zero for NAND-TM programs (and hence for Turing machines as well).
Moreover, as we will see in Chapter 11, there are uncomputable functions whose inputs are not programs, and hence for which the adjective “semantic” is not applicable.
Properties such as “the program contains the variable Yale” are sometimes known as syntactic properties. The terms “semantic” and “syntactic” are used beyond the realm of programming languages: a famous example of a syntactically correct but semantically meaningless sentence in English is Chomsky’s “Colorless green ideas sleep furiously.” However, formally defining “syntactic properties” is rather subtle and we will not use this terminology in this book, sticking to the terms “semantic” and “non-semantic” only.
Halting and Rice’s Theorem for other Turing-complete models
As we saw before, many natural computational models turn out to be equivalent to one another, in the sense that we can transform a “program” of one model (such as a \(\lambda\) expression, or a game-of-life configurations) into another model (such as a NAND-TM program). This equivalence implies that we can translate the uncomputability of the Halting problem for NAND-TM programs into uncomputability for Halting in other models. For example:
Let \(\ensuremath{\mathit{NANDTMHALT}}:\{0,1\}^* \rightarrow \{0,1\}\) be the function that on input strings \(P\in\{0,1\}^*\) and \(x\in \{0,1\}^*\) outputs \(1\) if the NAND-TM program described by \(P\) halts on the input \(x\) and outputs \(0\) otherwise. Then \(\ensuremath{\mathit{NANDTMHALT}}\) is uncomputable.
Once again, this is a good point for you to stop and try to prove the result yourself before reading the proof below.
We have seen in Theorem 7.11 that for every Turing machine \(M\), there is an equivalent NAND-TM program \(P_M\) such that for every \(x\), \(P_M(x)=M(x)\). In particular this means that \(\ensuremath{\mathit{HALT}}(M)= \ensuremath{\mathit{NANDTMHALT}}(P_M)\).
The transformation \(M \mapsto P_M\) that is obtained from the proof of Theorem 7.11 is constructive. That is, the proof yields a way to compute the map \(M \mapsto P_M\). This means that this proof yields a reduction from task of computing \(\ensuremath{\mathit{HALT}}\) to the task of computing \(\ensuremath{\mathit{NANDTMHALT}}\), which means that since \(\ensuremath{\mathit{HALT}}\) is uncomputable, neither is \(\ensuremath{\mathit{NANDTMHALT}}\).
The same proof carries over to other computational models such as the \(\lambda\) calculus, two dimensional (or even one-dimensional) automata etc. Hence for example, there is no algorithm to decide if a \(\lambda\) expression evaluates the identity function, and no algorithm to decide whether an initial configuration of the game of life will result in eventually coloring the cell \((0,0)\) black or not.
Indeed, we can generalize Rice’s Theorem to all these models. For example, if \(F:\{0,1\}^* \rightarrow \{0,1\}\) is a non-trivial function such that \(F(P)=F(P')\) for every functionally equivalent NAND-TM programs \(P,P'\) then \(F\) is uncomputable, and the same holds for NAND-RAM programs, \(\lambda\)-expressions, and all other Turing complete models (as defined in Definition 8.5), see also Exercise 9.12.
Is software verification doomed? (discussion)
Programs are increasingly being used for mission critical purposes, whether it’s running our banking system, flying planes, or monitoring nuclear reactors. If we can’t even give a certification algorithm that a program correctly computes the parity function, how can we ever be assured that a program does what it is supposed to do? The key insight is that while it is impossible to certify that a general program conforms with a specification, it is possible to write a program in the first place in a way that will make it easier to certify. As a trivial example, if you write a program without loops, then you can certify that it halts. Also, while it might not be possible to certify that an arbitrary program computes the parity function, it is quite possible to write a particular program \(P\) for which we can mathematically prove that \(P\) computes the parity. In fact, writing programs or algorithms and providing proofs for their correctness is what we do all the time in algorithms research.
The field of software verification is concerned with verifying that given programs satisfy certain conditions. These conditions can be that the program computes a certain function, that it never writes into a dangerous memory location, that is respects certain invariants, and others. While the general tasks of verifying this may be uncomputable, researchers have managed to do so for many interesting cases, especially if the program is written in the first place in a formalism or programming language that makes verification easier. That said, verification, especially of large and complex programs, remains a highly challenging task in practice as well, and the number of programs that have been formally proven correct is still quite small. Moreover, even phrasing the right theorem to prove (i.e., the specification) is often a highly non-trivial endeavor.
There is a universal Turing machine (or NAND-TM program) \(U\) such that on input a description of a Turing machine \(M\) and some input \(x\), \(U(M,x)\) halts and outputs \(M(x)\) if (and only if) \(M\) halts on input \(x\). Unlike in the case of finite computation (i.e., NAND-CIRC programs / circuits), the input to the program \(U\) can be a machine \(M\) that has more states than \(U\) itself.
Unlike the finite case, there are actually functions that are inherently uncomputable in the sense that they cannot be computed by any Turing machine.
These include not only some “degenerate” or “esoteric” functions but also functions that people have deeply cared about and conjectured that could be computed.
If the Church-Turing thesis holds then a function \(F\) that is uncomputable according to our definition cannot be computed by any means in our physical world.
Exercises
Let \(\ensuremath{\mathit{NANDRAMHALT}}:\{0,1\}^* \rightarrow \{0,1\}\) be the function such that on input \((P,x)\) where \(P\) represents a NAND-RAM program, \(\ensuremath{\mathit{NANDRAMHALT}}(P,x)=1\) iff \(P\) halts on the input \(x\). Prove that \(\ensuremath{\mathit{NANDRAMHALT}}\) is uncomputable.
Let \(\ensuremath{\mathit{TIMEDHALT}}:\{0,1\}^* \rightarrow \{0,1\}\) be the function that on input (a string representing) a triple \((M,x,T)\), \(\ensuremath{\mathit{TIMEDHALT}}(M,x,T)=1\) iff the Turing machine \(M\), on input \(x\), halts within at most \(T\) steps (where a step is defined as one sequence of reading a symbol from the tape, updating the state, writing a new symbol and (potentially) moving the head).
Prove that \(\ensuremath{\mathit{TIMEDHALT}}\) is computable.
Let \(\ensuremath{\mathit{SPACEHALT}}:\{0,1\}^* \rightarrow \{0,1\}\) be the function that on input (a string representing) a triple \((M,x,T)\), \(\ensuremath{\mathit{SPACEHALT}}(M,x,T)=1\) iff the Turing machine \(M\), on input \(x\), halts before its head reached the \(T\)-th location of its tape. (We don’t care how many steps \(M\) makes, as long as the head stays inside locations \(\{0,\ldots,T-1\}\).)
Prove that \(\ensuremath{\mathit{SPACEHALT}}\) is computable. See footnote for hint2
Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) and \(G:\{0,1\}^* \rightarrow \{0,1\}\) are computable functions. For each one of the following functions \(H\), either prove that \(H\) is necessarily computable or give an example of a pair \(F\) and \(G\) of computable functions such that \(H\) will not be computable. Prove your assertions.
\(H(x)=1\) iff \(F(x)=1\) OR \(G(x)=1\).
\(H(x)=1\) iff there exist two non-empty strings \(u,v \in \{0,1\}^*\) such that \(x=uv\) (i.e., \(x\) is the concatenation of \(u\) and \(v\)), \(F(u)=1\) and \(G(v)=1\).
\(H(x)=1\) iff there exist a list \(u_0,\ldots,u_{t-1}\) of non-empty strings such that strings\(F(u_i)=1\) for every \(i\in [t]\) and \(x=u_0u_1\cdots u_{t-1}\).
\(H(x)=1\) iff \(x\) is a valid string representation of a NAND++ program \(P\) such that for every \(z\in \{0,1\}^*\), on input \(z\) the program \(P\) outputs \(F(z)\).
\(H(x)=1\) iff \(x\) is a valid string representation of a NAND++ program \(P\) such that on input \(x\) the program \(P\) outputs \(F(x)\).
\(H(x)=1\) iff \(x\) is a valid string representation of a NAND++ program \(P\) such that on input \(x\), \(P\) outputs \(F(x)\) after executing at most \(100\cdot |x|^2\) lines.
Prove that the following function \(\ensuremath{\mathit{FINITE}}:\{0,1\}^* \rightarrow \{0,1\}\) is uncomputable. On input \(P\in \{0,1\}^*\), we define \(\ensuremath{\mathit{FINITE}}(P)=1\) if and only if \(P\) is a string that represents a NAND++ program such that there only a finite number of inputs \(x\in \{0,1\}^*\) s.t. \(P(x)=1\).3
Prove Theorem 9.13 without using Rice’s Theorem.
Let \(\ensuremath{\mathit{EQ}}:\{0,1\}^* :\rightarrow \{0,1\}\) be the function defined as follows: given a string representing a pair \((M,M')\) of Turing machines, \(\ensuremath{\mathit{EQ}}(M,M')=1\) iff \(M\) and \(M'\) are functionally equivalent as per Definition 9.14. Prove that \(\ensuremath{\mathit{EQ}}\) is uncomputable.
Note that you cannot use Rice’s Theorem directly, as this theorem only deals with functions that take a single Turing machine as input, and \(\ensuremath{\mathit{EQ}}\) takes two machines.
For each of the following two functions, say whether it is computable or not:
Given a NAND-TM program \(P\), an input \(x\), and a number \(k\), when we run \(P\) on \(x\), does the index variable
iever reach \(k\)?Given a NAND-TM program \(P\), an input \(x\), and a number \(k\), when we run \(P\) on \(x\), does \(P\) ever write to an array at index \(k\)?
Let \(F:\{0,1\}^* \rightarrow \{0,1\}\) be the function that is defined as follows. On input a string \(P\) that represents a NAND-RAM program and a String \(M\) that represents a Turing machine, \(F(P,M)=1\) if and only if there exists some input \(x\) such \(P\) halts on \(x\) but \(M\) does not halt on \(x\). Prove that \(F\) is uncomputable. See footnote for hint.4
Define a function \(F:\{0,1\}^* :\rightarrow \{0,1\}\) to be recursively enumerable if there exists a Turing machine \(M\) such that such that for every \(x\in \{0,1\}^*\), if \(F(x)=1\) then \(M(x)=1\), and if \(F(x)=0\) then \(M(x)=\bot\). (i.e., if \(F(x)=0\) then \(M\) does not halt on \(x\).)
Prove that every computable \(F\) is also recursively enumerable.
Prove that there exists \(F\) that is not computable but is recursively enumerable. See footnote for hint.5
Prove that there exists a function \(F:\{0,1\}^* \rightarrow \{0,1\}\) such that \(F\) is not recursively enumerable. See footnote for hint.6
Prove that there exists a function \(F:\{0,1\}^* \rightarrow \{0,1\}\) such that \(F\) is recursively enumerable but the function \(\overline{F}\) defined as \(\overline{F}(x)=1-F(x)\) is not recursively enumerable. See footnote for hint.7
In this exercise we will prove Rice’s Theorem in the form that it is typically stated in the literature.
For a Turing machine \(M\), define \(L(M) \subseteq \{0,1\}^*\) to be the set of all \(x\in \{0,1\}^*\) such that \(M\) halts on the input \(x\) and outputs \(1\). (The set \(L(M)\) is known in the literature as the language recognized by \(M\). Note that \(M\) might either output a value other than \(1\) or not halt at all on inputs \(x\not\in L(M)\). )
Prove that for every Turing machine \(M\), if we define \(F_M:\{0,1\}^* \rightarrow \{0,1\}\) to be the function such that \(F_M(x)=1\) iff \(x\in L(M)\) then \(F_M\) is recursively enumerable as defined in Exercise 9.10.
Use Theorem 9.15 to prove that for every \(G:\{0,1\}^* \rightarrow \{0,1\}\), if (a) \(G\) is neither the constant zero nor the constant one function, and (b) for every \(M,M'\) such that \(L(M)=L(M')\), \(G(M)=G(M')\), then \(G\) is uncomputable. See footnote for hint.8
Let \(\mathcal{F}\) be the set of all partial functions from \(\{0,1\}^*\) to \(\{0,1\}\) and \(\mathcal{M}:\{0,1\}^* \rightarrow \mathcal{F}\) be a Turing-equivalent model as defined in Definition 8.5. We define a function \(F:\{0,1\}^* \rightarrow \{0,1\}\) to be \(\mathcal{M}\)-semantic if there exists some \(\mathcal{G}:\mathcal{F} \rightarrow \{0,1\}\) such that \(F(P) = \mathcal{G}(\mathcal{M}(P))\) for every \(P\in \{0,1\}^*\).
Prove that for every \(\mathcal{M}\)-semantic \(F:\{0,1\}^* \rightarrow \{0,1\}\) that is neither the constant one nor the constant zero function, \(F\) is uncomputable.
In this question we define the NAND-TM variant of the busy beaver function (see Aaronson’s 1999 essay, 2017 blog post and 2020 survey (Aaronson, 2020) ; see also Tao’s highly recommended presentation on how civilization’s scientific progress can be measured by the quantities we can grasp).
Let \(T_{BB}:\{0,1\}^* \rightarrow \mathbb{N}\) be defined as follows. For every string \(P\in \{0,1\}^*\), if \(P\) represents a NAND-TM program such that when \(P\) is executed on the input \(0\) then it halts within \(M\) steps then \(T_{BB}(P)=M\). Otherwise (if \(P\) does not represent a NAND-TM program, or it is a program that does not halt on \(0\)), \(T_{BB}(P)=0\). Prove that \(T_{BB}\) is uncomputable.
Let \(\ensuremath{\mathit{TOWER}}(n)\) denote the number \(\underbrace{2^{\cdot^{\cdot^{\cdot^2}}}}_{n\text{ times}}\) (that is, a “tower of powers of two” of height \(n\)). To get a sense of how fast this function grows, \(\ensuremath{\mathit{TOWER}}(1)=2\), \(\ensuremath{\mathit{TOWER}}(2)=2^2=4\), \(\ensuremath{\mathit{TOWER}}(3)=2^{2^2}=16\), \(\ensuremath{\mathit{TOWER}}(4) = 2^{16} = 65536\) and \(\ensuremath{\mathit{TOWER}}(5) = 2^{65536}\) which is about \(10^{20000}\). \(\ensuremath{\mathit{TOWER}}(6)\) is already a number that is too big to write even in scientific notation. Define \(\ensuremath{\mathit{NBB}}:\mathbb{N} \rightarrow \mathbb{N}\) (for “NAND-TM Busy Beaver”) to be the function \(\ensuremath{\mathit{NBB}}(n) = \max_{P\in \{0,1\}^n} T_{BB}(P)\) where \(T_{BB}\) is as defined in Question 6.1. Prove that \(\ensuremath{\mathit{NBB}}\) grows faster than \(\ensuremath{\mathit{TOWER}}\), in the sense that \(\ensuremath{\mathit{TOWER}}(n) = o(\ensuremath{\mathit{NBB}}(n))\). See footnote for hint9
Bibliographical notes
The cartoon of the Halting problem in Figure 9.1 and taken from Charles Cooper’s website, Copyright 2019 Charles F. Cooper.
Section 7.2 in (Moore, Mertens, 2011) gives a highly recommended overview of uncomputability. Gödel, Escher, Bach (Hofstadter, 1999) is a classic popular science book that touches on uncomputability, and unprovability, and specifically Gödel’s Theorem that we will see in Chapter 11. See also the recent book by Holt (Holt, 2018) .
The history of the definition of a function is intertwined with the development of mathematics as a field. For many years, a function was identified (as per Euler’s quote above) with the means to calculate the output from the input. In the 1800’s, with the invention of the Fourier series and with the systematic study of continuity and differentiability, people have started looking at more general kinds of functions, but the modern definition of a function as an arbitrary mapping was not yet universally accepted. For example, in 1899 Poincare wrote “we have seen a mass of bizarre functions which appear to be forced to resemble as little as possible honest functions which serve some purpose. … they are invented on purpose to show that our ancestor’s reasoning was at fault, and we shall never get anything more than that out of them”. Some of this fascinating history is discussed in (Grabiner, 1983) (Kleiner, 1991) (Lützen, 2002) (Grabiner, 2005) .
The existence of a universal Turing machine, and the uncomputability of \(\ensuremath{\mathit{HALT}}\) was first shown by Turing in his seminal paper (Turing, 1937) , though closely related results were shown by Church a year before. These works built on Gödel’s 1931 incompleteness theorem that we will discuss in Chapter 11.
Some universal Turing machines with a small alphabet and number of states are given in (Rogozhin, 1996) , including a single-tape universal Turing machine with the binary alphabet and with less than \(25\) states; see also the survey (Woods, Neary, 2009) . Adam Yedidia has written software to help in producing Turing machines with a small number of states. This is related to the recreational pastime of “Code Golfing” which is about solving a certain computational task using the as short as possible program. Finding “highly complex” small Turing machine is also related to the “Busy Beaver” problem, see Exercise 9.13 and the survey (Aaronson, 2020) .
The diagonalization argument used to prove uncomputability of \(F^*\) is derived from Cantor’s argument for the uncountability of the reals discussed in Chapter 2.
Christopher Strachey was an English computer scientist and the inventor of the CPL programming language. He was also an early artificial intelligence visionary, programming a computer to play Checkers and even write love letters in the early 1950’s, see this New Yorker article and this website.
Rice’s Theorem was proven in (Rice, 1953) . It is typically stated in a form somewhat different than what we used, see Exercise 9.11.
We do not discuss in the chapter the concept of recursively enumerable languages, but it is covered briefly in Exercise 9.10. As usual, we use function, as opposed to language, notation.
- ↩
This argument has also been connected to the issues of consciousness and free will. I am personally skeptical of its relevance to these issues. Perhaps the reasoning is that humans have the ability to solve the halting problem but they exercise their free will and consciousness by choosing not to do so.
- ↩
A machine with alphabet \(\Sigma\) can have at most \(|\Sigma|^T\) choices for the contents of the first \(T\) locations of its tape. What happens if the machine repeats a previously seen configuration, in the sense that the tape contents, the head location, and the current state, are all identical to what they were in some previous state of the execution?
- ↩
Hint: You can use Rice’s Theorem.
- ↩
Hint: While it cannot be applied directly, with a little “massaging” you can prove this using Rice’s Theorem.
- ↩
\(\ensuremath{\mathit{HALT}}\) has this property.
- ↩
You can either use the diagonalization method to prove this directly or show that the set of all recursively enumerable functions is countable.
- ↩
\(\ensuremath{\mathit{HALT}}\) has this property: show that if both \(\ensuremath{\mathit{HALT}}\) and \(\overline{HALT}\) were recursively enumerable then \(\ensuremath{\mathit{HALT}}\) would be in fact computable.
- ↩
Show that any \(G\) satisfying (b) must be semantic.
- ↩
You will not need to use very specific properties of the \(\ensuremath{\mathit{TOWER}}\) function in this exercise. For example, \(\ensuremath{\mathit{NBB}}(n)\) also grows faster than the Ackerman function.
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 12/06/2023 00:07:11
Copyright 2023, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.